牛客月赛43

Posted 2022-02-05 斗奋力努

牛客小白月赛43

2202年还没写过题解，就写随手写一份牛客题解吧

本场考点：dfs、思维
中文题面就是好读
A、满意的数字

思路：n才1000，我们直接预处理一下1~n，然后前缀和pre[i]代表前i个数字中“满意的数字”个数。

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,pre[N];
vector<int>num[N];

void build()
    for(int i=1;i<=1000;i++)
        for(int j=1;j<=i;j++)
            if(i%j==0) num[i].push_back(j);
        
        int pos1=num[i].size();
        int pos2=(pos1+1)/2;
        if(num[i][pos1-1]%num[i][pos2-1]==0) pre[i]=pre[i-1]+1;
        else pre[i]=pre[i-1];
    


void solve()
    scanf("%d\\n",&n);
    printf("%d\\n",pre[n]);


int main()
    build();
    int t;scanf("%d",&t);
    while(t--) solve();

B、牛牛变魔术
题意：给a、b，是否可以得到target
操作：
(a-x)*2,(b+x)*2 (a-x)>=0
(a+x)*2,(b-x)*2 (b-x)>=0

思路：
①：a、b是否初始就有一个等于target，有输出0
②：target是否为奇数，此时奇数一定不可达，输出-1
③：看（a+b）什么时候大于等于target

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,target;

void solve()
    scanf("%lld%lld%lld",&a,&b,&target);
    if(a==target||b==target) puts("0");return;
    if(target%2==1) puts("-1");return;
    ll nu=1,now=(a+b)*2;
    while(now<target)
        nu++;
        now*=2;
    
    printf("%lld\\n",nu);


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

C、木棍游戏

思路：n的范围才8，直接无脑dfs就行了

#include<bits/stdc++.h>
using namespace std;
int n;
double a[10],S=-1;

bool cek(double l1,double l2,double l3)
    if(l1==0||l2==0||l3==0) return false;
    bool f1=((l1+l2)>l3)&&(abs(l1-l2)<l3);
    bool f2=((l1+l3)>l2)&&(abs(l1-l3)<l2);
    bool f3=((l2+l3)>l1)&&(abs(l2-l3)<l1);
    return f1&&f2&&f3;


double get_S(double l1,double l2,double l3)
    double p=(l1+l2+l3)/2;
    return sqrt(p*(p-l1)*(p-l2)*(p-l3));


void dfs(int pos,double l1,double l2,double l3)
    if(cek(l1,l2,l3))S=max(S,get_S(l1,l2,l3));
    if(pos==n+1) return;
    dfs(pos+1,l1+a[pos],l2,l3);//加到第1根
    dfs(pos+1,l1,l2+a[pos],l3);//加到第2根
    dfs(pos+1,l1,l2,l3+a[pos]);//加到第3根
    dfs(pos+1,l1,l2,l3);//不要这一根


int main()
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lf",&a[i]);
    dfs(0,0,0,0);
    if(S==-1) puts("-1");
    else printf("%.1lf\\n",S);

D、有趣的区间

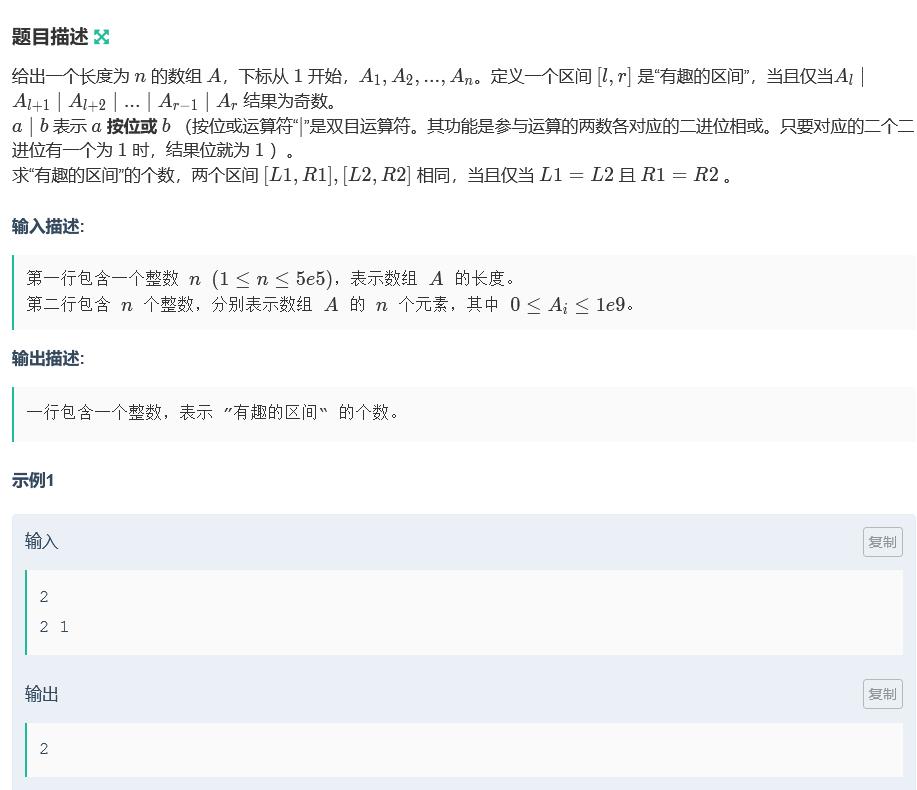
题意：问有多少个区间，区间中所有元素的或值为奇数(就是区间至少有一个元素是奇数)
思路：我们记录上一个奇数的位置pos，然后每次加上pos就行了。
①：当前a[i]是奇数，此时位置pos前面有pos个数（包括自己），选前面的是与当前数组合就有pos种，所以sum+=pos;
②：当前a[i]是偶数，为了做出贡献，我们只能将区间[pos+1，i]中所有数都选了，此时就跟上一个奇数连接起来，那么贡献就跟奇数一样了，也是sum+=pos
综上①②，每次不断更新上一个奇数位置pos，每次都是sum+=pos

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
ll n,a[N],sum,pos;

int main()
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)
        scanf("%lld",&a[i]);
        a[i]%=2;
        if(a[i]==1) pos=i;
        sum+=pos;
    
    printf("%lld\\n",sum);

E、满意的集合

思路：
好像直接dp就行了，$$dp[i][j]只选1到i中的数，\%3=j的方案数$$
选数遵守%3=(0,1,2)的三种选法。随后看可以组成多少对就行了。

        ll use1=1*i%3,nu1=(cnt[i]+2)/3;
        ll use2=2*i%3,nu2=(cnt[i]+1)/3;
        ll use3=3*i%3,nu3=(cnt[i]+0)/3+1;
        //这里nu1、nu2、nu3是组成多少对，不能用减法
        //例如cnt[i]=0 
        //加法：nu1=(cnt[i]+2)/3=(0+2)/3=0;
        //减法：nu1=(cnt[i]-1)/3+1=(0-1)/3+1=1
        //因为cnt[i]=0，实际是只能组成0对的，如果用减法会得到1对，不符合实际情况

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll cnt[11],dp[11][3];

int main()
    for(ll i=1;i<=9;i++) scanf("%lld",&cnt[i]);
    dp[0][0]=1;
    for(ll i=1;i<=9;i++)
        ll use1=1*i%3,nu1=(cnt[i]+2)/3;
        ll use2=2*i%3,nu2=(cnt[i]+1)/3;
        ll use3=3*i%3,nu3=(cnt[i])/3+1;
        for(ll j=0;j<3;j++)
            dp[i][(j+use1)%3]=(dp[i][(j+use1)%3]+dp[i-1][j]*nu1)%mod;
            dp[i][(j+use2)%3]=(dp[i][(j+use2)%3]+dp[i-1][j]*nu2)%mod;
            dp[i][(j+use3)%3]=(dp[i][(j+use3)%3]+dp[i-1][j]*nu3)%mod;
        
    
    printf("%lld\\n",dp[9][0]);

F、全体集合
题意：在一个联通图中，有k个人，每秒所有人都要移动，问最后是否可以到达同一点。
思路：我的想法是以1为根(集合点)，看每个人到达节点1的步数是否奇偶性相同，相同YES，不同NO
需要注意的是，题目给的边好像有点多，所以一个人可能走奇数到节点1、也可能走偶数步到节点1，就设dp[i][0\\1]，代表奇偶就行了，最后看是否满足上面想法就行了。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,k,m,ans[N];
vector<int>edge[N];
bool dp[N][2];

void dfs(int u,int fa,int type)
    dp[u][type]=true;
    for(int i=0;i<edge[u].size();i++)
        int v=edge[u][i];
        if(dp[v][type^1]) continue;
        if(v==fa) continue;
        dfs(v,u,type^1);
    


int main()
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=m;i++)
        int u,v;scanf("%d%d",&u,&v);
        edge[u].push_back(v);
        edge[v].push_back(u);
    
    for(int i=1;i<=k;i++) scanf("%d",&ans[i]);
    dfs(1,0,1);
    bool flag1=true,flag2=true;
    for(int i=1;i<=k;i++)
        flag1=flag1&&dp[ans[i]][0];
        flag2=flag2&&dp[ans[i]][1];
    
    if(flag1||flag2) puts("YES");
    else puts("NO");