12月学习进度11/31——高等数学从微分的发展史看微分的本质

Posted 2022-02-01 fu_GAGA

学习参考：微分、导数、积分，这三者之间，有没有联系？

(以下学习内容和截图全部来自于以上链接）

---

0. 矛盾问题引入

$dx$ 为什么需要为0时为0（可以当做0消除），不需要为0时不为0（不当做0进行约分）？

1. 微分的本质

微分本质是一个微小的线性变化量，是用一个线性函数作为原函数变化的逼近（或者近似）。

我们定义 $dy=f^{\prime }(x)△x$
$△y$ 是原函数的变化，则 $dy$ 就是对函数值变化的逼近
由 $dy=f^{\prime }(x)△x$ 可知，$dy$ 是 $△x$ 的线性函数

• $dy$ 不仅仅是微分符号，有真正含义和具体值 $dy=f^{\prime }(x)△x$
• 微分在一点处，用一个线性函数的变化逼近函数的变化

令 $y$ 即 $f(x)$ 为 $x$ ，则可得：
$$dx=1\ast △x=△x$$
【通俗说法】$dx$、$dy$ 就是 $y$ 和 $x$ 的一种变化量，有具体的值，只是由于 $△x$ 有趋于零的性质，而变得特殊了一些。

由 $dy=f^{\prime }(x)△x$ 可得导数与微分的关系
$$\frac{dy}{dx}=f^{\prime }(x)$$

2. 微分的发展历史

以上按照 极限→导数→微分 的顺序来理解微分的本质，但历史没有如此的顺序性：

• 极限发明前：古典微积分（无穷小量的概念）
• 极限发明后：极限微积分（基于极限思想将导数和微分的概念都重新建立了一遍）

2.1. 古典微分

迫切需要微小的变换量

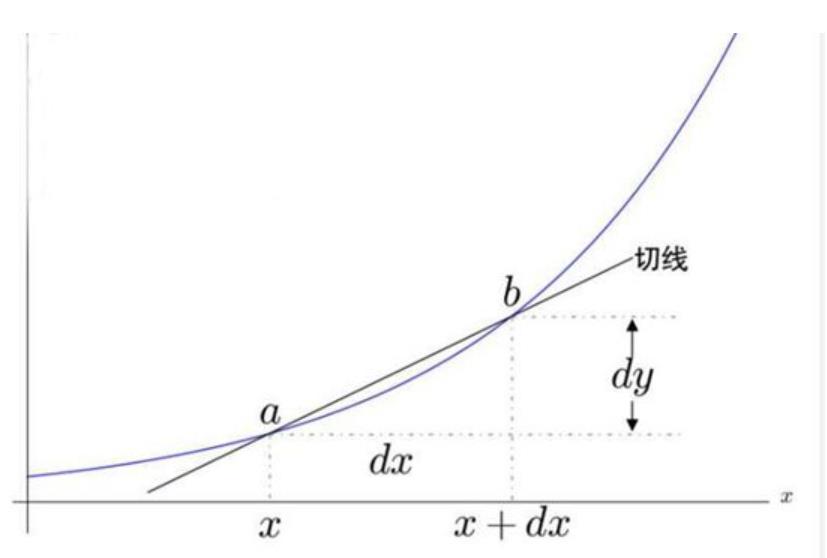
【数学家当时定义切线】

1. 定义 $dy$ 是函数值 $y$ 的变化量 ，$dx$ 是自变量 $x$ 的变化量
2. 当上图中 $b$ 点足够接近 $a$ 点（即 $dx$ 无穷小）时，割线就会无限与切线重合
3. 定义 $dy$ 为 $y$ 的微分，$dx$ 为 $x$ 的微分（微分即微小的变化量）
4. 由上图知，$\frac{dy}{dx}$ 是切线的斜率，定义其为导数（即因变量微分与自变量微分之比为导数，所以导数又称为微商）

【漏洞】

1. 两点才能确定一条直线，如果b点都与a点重合了，那怎么会把切线给确定出来呢？
2. 如果b点与a点不重合，那dx总会表示一段距离，那割线总会与函数有两个交点，有两个交点又怎么称之为切线呢？

【本质原因】 无穷小量没有得到明确定义及解释

2.2. 极限微分学

【极限的定义】

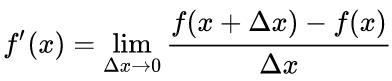
【上述问题的解决】

1. 无穷小：极限为0的量
2. 切线：割线的极限

2.3. 两者的重大差别

我们现在所学的体系，是按照先极限、再通过极限定义导数、再通过导数定义微分这个次数来的。但是在历史发展中，是先有的微分（即先定义出dy），然后根据需要（为了解决切线问题）定义出导数的。

3. 微分与导数的区别

• 导数：是指函数在某一点处变化的快慢,是一种变化率。
• 微分：是指函数在某一点处（趋近于无穷小）的变化量，是一种变化的量。

对于多元函数而言，全微分就是指在各个自变量处的微分的和。也就是说总的变化量指各个分变化量的和，比如二元函数 $dz=z_x\ast dx+z_y\ast dy$。

---

妙妙妙妙妙~