关于取模运算的小技巧

Posted 2022-01-31 程序员茶馆

取模运算的定义：a%b=a-b*(a/b)，其中b≠0。

众所周知，相对于位运算而言除法运算是个相当奢侈的操作，因此在需要大量使用取模运算且对性能有要求的情况下，若满足b为2的整数次幂（即b=1<<k，k为整数）时，可用一个特殊的小技巧将取模运算转化为位运算，即：a%b=a&(b-1)，且b=1<<k（k为整数）。为什么呢？

我们以8为例，8的二进制表示为下图：

在3号位以上均为8的倍数，即对8取模均为0，因此对取模有贡献的为3号位以下的。

根据上述公式：b-1=8-1=7,7的二进制表示为下图：

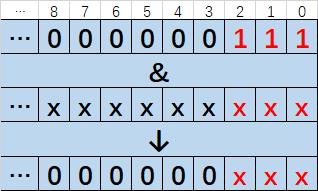
此时任何1~7的数与7进行按位与（&）操作，均为其本身，即恰好是对8取模的结果，如下图：

 

参考：

1.https://www.quora.com/Why-is-the-modulo-operator-expensive-How-do-you-replace-the-modulo-operation-with-equivalent-but-less-expensive-operations

2.https://blog.csdn.net/akakakak250/article/details/54377664?spm=1001.2014.3001.5502