:初出茅庐初级篇 - 2.3 动态规划
Posted 辉小歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了:初出茅庐初级篇 - 2.3 动态规划相关的知识,希望对你有一定的参考价值。
目录
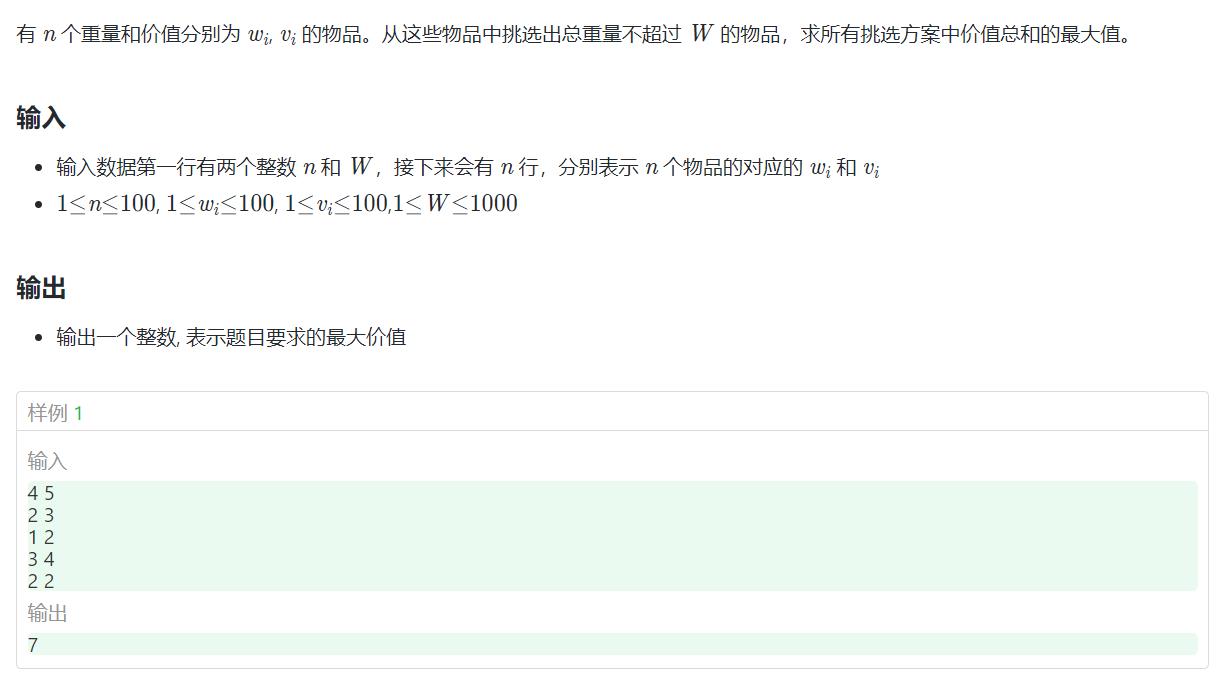
218. 01背包问题【经典模型】
https://www.papamelon.com/problem/218
状态表示: f[i][j] 表示从前i个物品中选 总体积不超过j的最大价值
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[110][N],n,m,w[N],v[N];
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
f[i][j]=f[i-1][j];
if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
cout<<f[n][m];
return 0;
其实可以边读入边计算。
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[110][N],n,m,w[N],v[N];
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
for(int j=0;j<=m;j++)
f[i][j]=f[i-1][j];
if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
cout<<f[n][m];
return 0;
优化空间至一维。
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N],n,m,w[N],v[N];
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
for(int j=m;j>=v[i];j--)
f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m];
return 0;
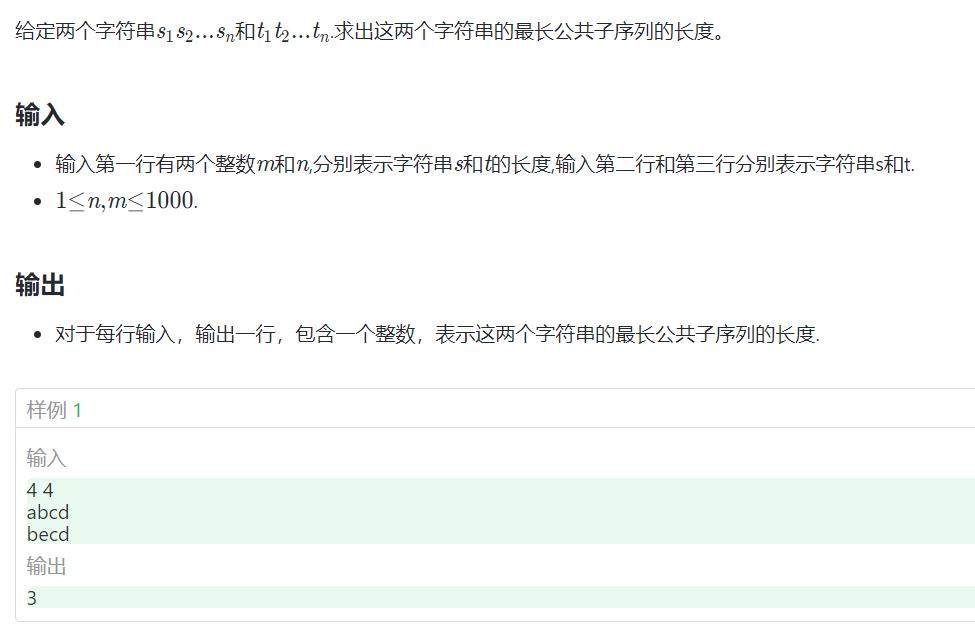
220. 最长公共子序列问题【经典模型】
https://www.papamelon.com/problem/220
状态表示: f[i][j] 表示a的前i个字符 和 b的前j个字符的最长公共子序列个数
- a的第i个不选,b的第j个也不选
f[i-1][j-1] - a的第i个选,b的第j个不选
f[i][j-1] - a的第i个不选,b的第j个选
f[i-1][j] - a的第i个选,b的第j个也选。这时候就要判断
a[i]是否等于b[j]如果相等则f[i-1][j-1]+1
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int f[N][N],n,m;
char a[N],b[N];
int main(void)
cin>>n>>m>>a+1>>b+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
f[i][j]=max(f[i-1][j-1],f[i][j-1],f[i-1][j]);
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
cout<<f[n][m]<<endl;
return 0;
其实都不选的状态可以不用写,因为其他的几种状态就已经包含了。
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int f[N][N],n,m;
char a[N],b[N];
int main(void)
cin>>n>>m>>a+1>>b+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
f[i][j]=max(f[i][j-1],f[i-1][j]);
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
cout<<f[n][m]<<endl;
return 0;
219. 完全背包问题【经典模型】

https://www.papamelon.com/problem/219
#include<bits/stdc++.h>
using namespace std;
const int N=10100;
int f[110][N],n,m,w[N],v[N];
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
f[i][j]=f[i-1][j];
if(j>=v[i]) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
cout<<f[n][m];
return 0;
#include<bits/stdc++.h>
using namespace std;
const int N=10100;
int f[N],n,m,w[N],v[N];
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
for(int j=v[i];j<=m;j++)
f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m];
return 0;
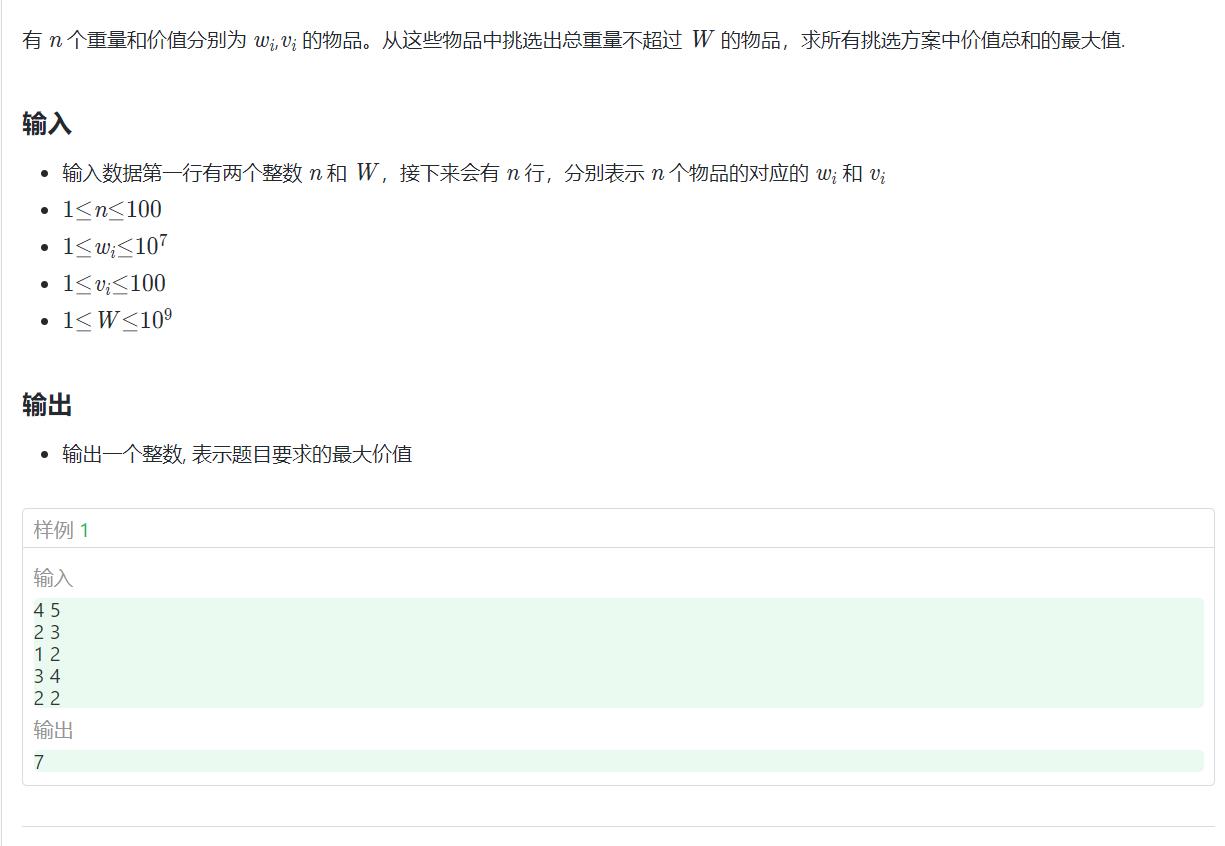
221. 01背包问题之 2【经典模型】
https://www.papamelon.com/problem/221
通过分析,你会发现我们的体积是太大了,但是有一个就是我们的价值和很小的。
故f[i][j] 表示再前i中选总价值为j 的最小体积 其本质基于贪心的思维,对于同样价值的物品我们肯定是希望浪费的体积越小越好。
最后我们在按总价值从大到小枚举,第一个体积小于我们背包总体积的就是答案。
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int f[110][N],n,m,w[N],v[N];
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
memset(f,0x3f,sizeof f);
for(int i=0;i<=n;i++) f[i][0]=0;
for(int i=1;i<=n;i++)
for(int j=0;j<N;j++)
f[i][j]=f[i-1][j];
if(j>=w[i]) f[i][j]=min(f[i][j],f[i-1][j-w[i]]+v[i]);
for(int i=N-1;i>=0;i--)
if(f[n][i]<=m)
cout<<i;
break;
return 0;
222. 多重部分和问题【中 有意思】

https://www.papamelon.com/problem/222
f[i][j] 表示前i个数,总和为j。第i类剩余的个数
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const int M=1e5+10;
int f[N][M],a[N],cnt[N],n,m;
//f[i][j] 表示前i个数,总和为j。第i类剩余的个数
int main(void)
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>cnt[i];
memset(f,-1,sizeof f);
for(int i=1;i<=n;i++) f[i][0]=cnt[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
if(f[i-1][j]>=0) f[i][j]=cnt[i];//不拿
if(j>=a[i]&&f[i][j-a[i]]>0) f[i][j]=max(f[i][j],f[i][j-a[i]]-1);//拿
if(f[n][m]>=0) puts("Yes");
else puts("No");
return 0;
223. 最长上升子序列问题【经典模型】

https://www.papamelon.com/problem/223
f[i] 表示以i结尾的最长上升子序列
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N],n,a[N];
int main(void)
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
f[i]=1;
for(int j=1;j<i;j++)
if(a[j]<a[i]) f[i]=max(f[i],f[j]+1);
int ans=0;
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
cout<<ans;
return 0;
以上是关于:初出茅庐初级篇 - 2.3 动态规划的主要内容,如果未能解决你的问题,请参考以下文章