数字与数学7：幂的问题

Posted 2022-01-26 纵横千里，捭阖四方

LeetCode231题，让你判断一个数是否为2的幂

LeetCode326题，让你判断一个数是否为3的幂

LeetCode342题，让你判断一个数是否为4的幂

这几个题是一个模子里复制出来的，但是解法还是有很大区别的，我们看一下。

1.判断是否为2的次幂

常规的思路可能是i从1循环到根号n, i每次*2或者高级一点的写法<<1 左移1，这种常规的解题思路时间复杂度是O(logn)，这个题有个经典的解法，直接判断(n & (n - 1)) == 0即可，为什么这样呢？看一下下面的规律：

 如果把上面图中2的幂次方都减去1：

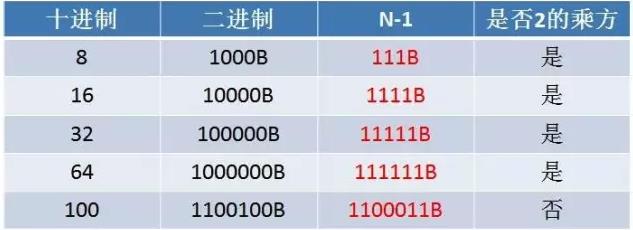
 2的幂次方原本只有最高位是1，其它位都是0，而它对应的2的幂次方减1 少了1位并且每一位都是1

所以结论就是：

class Solution 
    public boolean isPowerOfTwo(int n) 
        return n > 0 && (n & (n - 1)) == 0;
    

2.是否为3的幂

一个不能再朴素的做法是将 nn 对 33 进行试除，直到 nn 不再与 33 呈倍数关系，最后判断 nn 是否为 3^0 ==1 即可。

class Solution 
    public boolean isPowerOfThree(int n) 
        if (n <= 0) return false;
        while (n % 3 == 0) n /= 3;
        return n == 1;
    

有些地方说可以使用约束，但是不知道效率怎么样，这里就不写了，这里介绍另一种偷懒的方法

使用 static 代码块，预处理出不超过 int 数据范围的所有 3 的幂，这样我们在跑测试样例时，就不需要使用「循环/递归」来实现逻辑，可直接 O(1)查表返回。

class Solution 
    static Set<Integer> set = new HashSet<>();
    static 
        int cur = 1;
        set.add(cur);
        while (cur <= Integer.MAX_VALUE / 3) 
            cur *= 3;
            set.add(cur);
        
    
    public boolean isPowerOfThree(int n) 
        return n > 0 && set.contains(n);
    

3.是否为4的幂

这个题有人总结出一些规律，但是我感觉记规律没什么用，我们还是用能练习思维的比较好，

一个数 nn 如果是 4 的幂，等价于 nn 为质因数只有 2 的平方数。因此我们可以将问题其转换：判断 sqrtn 是否为 2的幂即可。

class Solution 
    public boolean isPowerOfFour(int n) 
        if (n <= 0) return false;
        int x = (int)Math.sqrt(n);
        return x * x == n && (x & -x) == x;