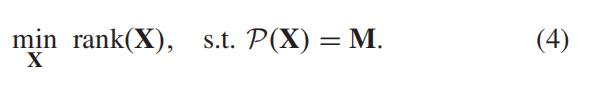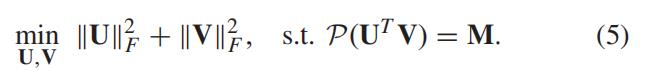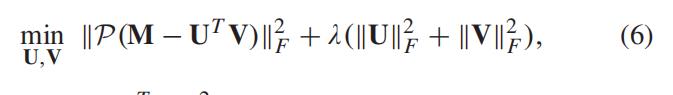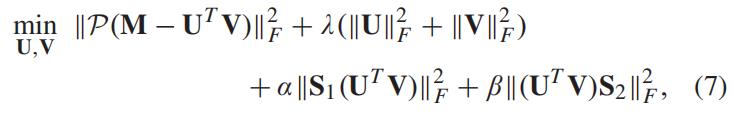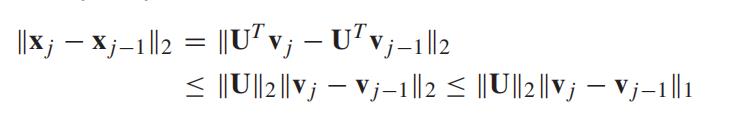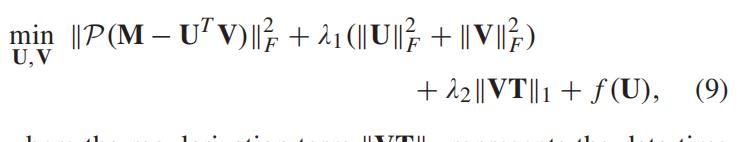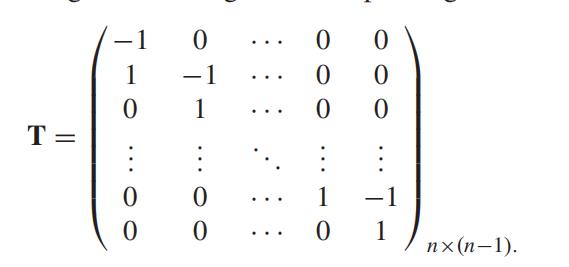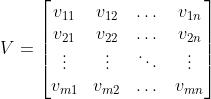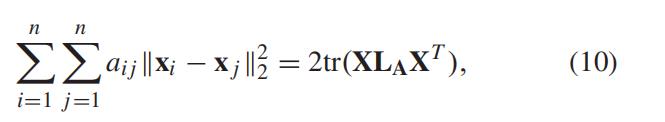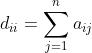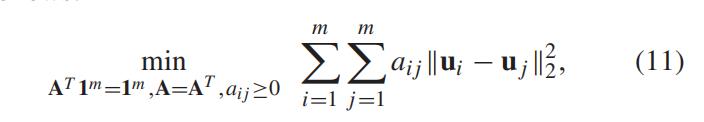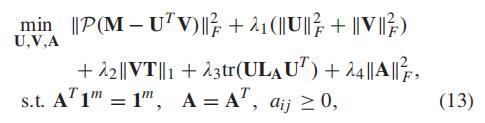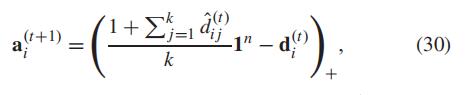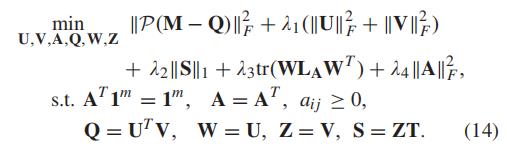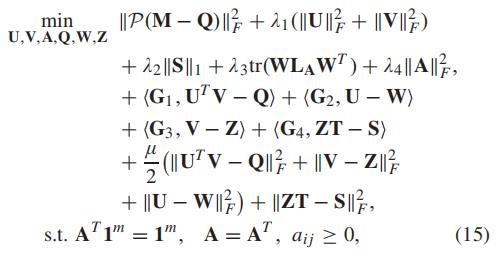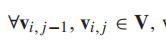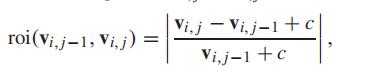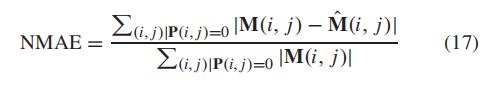论文笔记 Traffic Data Reconstruction via Adaptive Spatial-Temporal Correlations

Posted 2022-01-25 UQI-LIUWJ

IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS 2019

0 摘要

        数据缺失仍然是交通信息系统中的一个难点和重要问题，严重制约了智能交通系统（ITS）在交通监控方面的应用，如交通数据采集、交通状态估计和交通控制。在过去十年中提出了许多交通数据插补方法。然而，缺乏足够的时间变化特征分析和空间相关性测量导致完井精度有限，给智能交通系统带来了重大挑战。

        利用交通网络数据的低秩性质和时空相关性，本文提出了一种基于低秩矩阵分解重构缺失交通数据的新方法，通过分解因子矩阵阐述了交通矩阵的潜在含义。 .

        为了进一步利用道路链接的时间演化特征和空间相似性，我们设计了时间序列约束和自适应拉普拉斯正则化空间约束来探索与道路链接的局部关系。在六个真实世界交通数据集上的实验结果表明，我们的方法优于其他方法，并且可以针对各种结构损失模式成功准确地重建道路交通数据。

1 introduction

        目前有许多插补方法来解决缺失数据问题。 传统方法涉及诸如历史插补 [3] 和样回归插补 [4] 方法等技术。

        [3]:Nearest neighbor imputation for survey data,” 2000

        [4]:“PPCA-based missing data imputation  for traffific flflow volume: A systematical approach,” 2009

        最近也有一些基于低秩的研究工作来提高缺失交通数据插补的性能。 然而，将这些方法应用于交通数据重建只能获得有限的精度，因为不能考虑或充分利用交通网络特征，如道路网络拓扑、序列时间特征。 具体来说，当大量数据丢失时，它们的恢复精度仍然很低。

        事实上，交通数据中有很多相关性。

        交通数据时间相关性需要考虑小时与小时、间隔与间隔的关系，具有变化特征，即平滑或突变。

        至于空间相关性，它不仅存在于相邻链路中，而且存在于具有相同道路物理属性特征、信号控制设置和位置功能属性的非相邻空间链路中。

        然而，在以前的插补方法中并没有完全探索这些相关性。

        如图 1（a）所示，速度数据和车流量数据的曲线都具有连续平滑的趋势，并且在几个时间间隔内急剧减少或增加。

                我们认为这种现象的出现是由于数据采集的频率、道路交通事故、城市交通网络的特征（如红绿灯和频繁的状态转换）、数据采集的噪声等多种因素造成的。

        大多数数据重建方法都考虑了连续可变性，而没有考虑突变的实际存在。

                

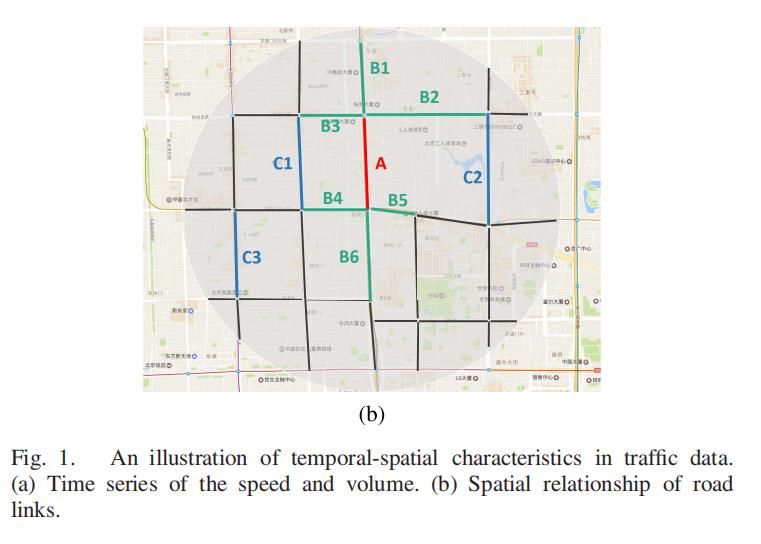
        此外，如图1(b)所示，道路A的道路交通与直接相连的路段B1、B2、B3、B4、B5、B6以及非相邻路段C1、C2，C3密切相关。

        这种相似性不仅体现在路网拓扑结构上，还体现在真实数据的相关性上，仅仅利用固定的拓扑关系来挖掘交通数据的内在原理是不够的。

         为了解决上述缺点，本文提出了一种创新的交通数据重建方法，称为时间和自适应空间约束低秩（TAS-LR Temporal and  Adaptive Spatial Constrained Low Rank ）。

         所提出的方法通过使用低秩表示模型来利用交通数据的全局特征，以及自适应的时空约束来利用交通数据的局部特征。

        与现有的矩阵补全（MC）方法相比，TAS-LR 的适应性更强，因为它独立于特定的交通网络，并且在实际交通数据上表现出令人满意的补全精度。 此外，为了达到相同的精度水平，TAS-LR 在相同的精度水平下需要更少的交通数据。 本文的主要贡献包括：

• TAS-LR 将交通数据分解为两个潜在特征矩阵：
  • 一个矩阵代表潜在空间特征 描述道路链接的静态特性
  • 另一个矩阵表示描述时间变化特征的全局环境特征。
• TAS-LR 通过对潜在时间特征矩阵施加稀疏约束，根据交通数据的平滑变化精确而稳健地表征突然变化。
•  TAS-LR 利用空间邻居选择机制作为辅助约束来提高交通数据重建的适应性。

2 related work

        常用的交通数据补全方法有历史插值法和邻域插值法[3]。

“Nearest neighbor imputation for survey data,” 2000

        历史插值法通过已知数据点 不同时间的多个观测值的平均值来预测缺失值。

        对于邻域插值方法，缺失点是通过同一时间相邻点的值来推断的。使用 k 最近邻 (KNN) [8] 进行加权、插值是合理的。但是对于交通数据矩阵，很难直接应用 KNN，因为行（或列）是任意排序的（例如基于道路名称）。所以矩阵中最近的元素可能几乎没有对应关系。此外，这种方法也不适用于邻域内数据点缺失的情况。

“Nearest neighbor pattern classifification,” 1967

        回归插补方法根据同一时间收集的周围已知数据/同一位置收集的过去时刻观测值，应用数学插值算法来重构缺失值[4]。

PPCA-based missing data imputation for traffific flflow volume: A systematical approach 2009

        一般采用线性回归方法[9]构建缺失数据，计算实时速度数据与其对应的时间/空间数据之间的线性相关系数。

“Real-time traffific data screening and reconstruction, 2003

         这些方法的插补性能很大程度上取决于缺失点的周围数据。 也就是说，这些方法只利用了交通量数据的一部分相关性，无法考虑全局特征。 因此，它们的性能并不令人满意，尤其是当缺失数据的比例很高时。  

        压缩感知 (CS) 是一种技术，它可以在向量稀疏的情况下从样本子集中准确地恢复向量 [7]。它考虑了某些域中信号的稀疏性或可压缩性，这允许从相对较少的测量中确定整个信号。        

“Compressed sensing, 2003

        因此，CS 可以应用于补全缺失值的基于矩阵的问题。基于矩阵的方法利用二维全局信息来估计丢失的数据。

        例如，在存在缺失条目的情况下，非负矩阵分解 (NMF) [10]、[11] 可以用于恢复缺失值，通过交替非负最小二乘。这种方法虽然与SVD非常相似，但这种方法坚持非负因子矩阵，缺乏可扩展性，无法面对大量缺失数据。

Algorithms for non-negative matrix factorization, 2001

Near-optimal signal recovery from random projections: Universal encoding strategies? 2006

        稀疏正则化 SVD (SRSVD) [5] 创建了一个类似于 SVD 的矩阵分解，并应用正则化方法来优化对缺失数据的估计。

        稀疏正则化矩阵分解 (SRMF) [5] 是一种用于交通矩阵插值、交通预测和异常检测的新型时空压缩感知框架，它利用交通数据的低秩性质及其时空特性来估计丢失的交通数据。

Spatio-temporal  compressive sensing and Internet traffific matrices 2012

        此外，提出了一种基于幂律的压缩感知方法 [12] 来重建端到端的网络流量。  

“A power laws-based reconstruction  approach to end-to-end network traffific, 2013

        由于交通数据具有链路间周期性变化和空间相似性的特点，交通数据通常具有低秩性质。 因此，低秩矩阵补全方法非常适合其重构。  

        低秩矩阵完成 (MC) [13] 利用矩阵的低秩结构来恢复丢失的条目。它已被用于各种研究领域，例如协同过滤、计算机视觉和无线传感器网络等。

“Exact matrix completion via convex  optimization,” 2009

        最近，研究人员提出了解决低秩矩阵补全问题的有效算法，这些算法分为三类：

1）基于范数的方法，例如奇异值阈值算法（SVT）[14]，它是一种迭代算法用于求解近似矩阵补全问题的凸松弛；

“A singular value thresholding algorithm for matrix completion,” 2010

2) 基于子空间投影的方法，例如 Grassman Manifold 上的梯度下降算法 (OPTSPACE) [15]，它基于奇异值分解和局部流形优化；

“Matrix completion from a  few entries,” 2010

3）基于矩阵分解的方法，例如Low-rank Matrix Fitting algorithm (LMaFit) [16]，它是一种低秩分解模型

“Solving a low-rank factorization  model for matrix completion by a nonlinear successive over-relaxation algorithm,” 2012

        然而，上述方法没有完全或同时利用交通数据中的时间和空间关系。 数据丢失率高时，补全精度有提升空间  

        还有其他研究将数据制定为张量形式来估计缺失值。

         张量是一个多维数组，它可以保留数据的多维性质，并在张量的每一维中提取潜在的因素。

        首先提出了一种高精度低秩张量完成算法（HaLRTC）[17]，以估计张量形式的视觉数据的缺失值。

        然后提出了一种基于张量分解的插补方法（TDI）[18]来估计交通运输中的缺失值。

         然而，当数据丢失率高时，其重建性能显着下降。 此外，它的求解问题是一个 NP-hard 问题 [19]。

        因此，基于低秩张量分解的补全方法一般不能达到满意的精度。

        实际上，由于不确定噪声的因素，实际交通矩阵通常不是严格的低秩矩阵。

        因此，现有的基于 CS 和 MC 的方法不能直接应用于交通数据完成。

        在本文中，受NMF理论的启发，我们提出了一种以时间序列变化特征为特征的方法，并采用自适应空间邻域选择机制来优化完成问题。  

3 preliminary 

3.1 问题定义

我们记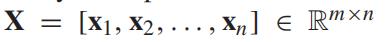为交通数据矩阵，其中行和列分别表示空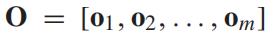间和时间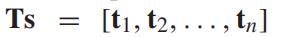

 

        由于一般来说收集到的交通数据矩阵不可能是一个完整的矩阵，所以我们使用一个掩盖操作符P来表示这个不完整矩阵的过程 

        

        此时矩阵M就是一个不完整矩阵，只有一部分位置有数值

        P操作符也可以表述成逐元素矩阵乘积（哈达玛积）的形式

         

         这时矩阵P可以被定义为：

         

         我们的目标是重构出一个完整的交通矩阵。一个直观方法是解决秩最小化问题：

        

         由于最小化秩是一个NP-难的问题，我们用rank(X)的凸包，核范数来代替，得到一个凸的和更易于计算的近似值。核范数被定义为其奇异值的总和。

        于是(4)中的目标函数可以被替换为：

         

        但是，由于基本的低秩模型没有考虑内部数据元素的空间和时间关系，因此在交通数据丢失率较高时表现不佳。

3.2 矩阵分解和时空限制

        这里引入了交通矩阵的时空分解，并在因子矩阵上添加了约束，以改进矩阵重构。

        令 ，我们有两个因子矩阵 U 和 V，其中 U ∈ R^r×m ，V ∈ R^r×n。

        我们将U视为对象的潜在空间特征矩阵，其每一列对应某一空间位置的静态描述属性。

        我们将V视为潜在的全局环境特征矩阵，其每一列对应某一空间位置在不同时间间隔的状态描述。

        因此，交通矩阵X 可以看作是对象的静态特性和动态特性相互作用的结果。

        具体来说，这里的路段特征可以是土地利用属性、道路程度、车道数和路面粗糙度等因素，这些路段的特征描述构成了空间特征矩阵U。

        同理，同一个城市的所有路段 共享同一个动态的外部环境，如天气条件、城市人口生活和工作的规律等。

        矩阵分解方法不仅可以避免核范数的多次高开销计算（矩阵奇异值分解是O(n^3)的复杂度），而且有助于直接对因子矩阵施加时空约束。  

        于是，我们的目标函数从可以变成

        

        使用拉格朗日算子,（5）式的约束条件也写入目标函数中，于是有：

        

                这是数据完成的基本低秩模型，它仅利用全局低秩属性

        结合X的行和列的局部关系，（这个局部关系可以反映交通数据的内在属性）。 通常，时空约束模型被公式化为

        

        其中S1和S2分别代表先验空间约束矩阵和时间约束矩阵，α和β是平衡参数。

         在本文中，我们将直接对潜在特征矩阵施加约束以增强时空数据结构。

4 时间和自适应空间约束低秩模型 TAS-LR

        在这里正式定制了我们的模型 TAS-LR。  

        给定一个动态路网交通矩阵 X ∈ Rm×n，行数和列数分别对应于路段和时间间隔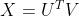，。 我们希望实现以下目标函数：

        

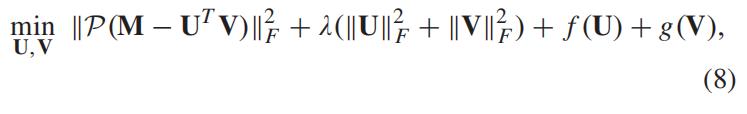
        其中 f (·) 和 g(·) 分别是作用于因子矩阵的空间和时间约束函数。

        该模型通过考虑时间突变特征引入时间鲁棒约束，并结合自适应空间相似性寻找算子解决交通矩阵完成问题。

        为了后文方便起见，列出了所有的符号：

        

4.1 Temporal Variation Characteristics 时间变化特征

        交通状态的变化是一个渐进、连续的过程，但实际中交通数据的时间序列通常既有连续变化又有突变。
         原因之一可能是数据采集的时间频率，即数据采集的频率越高，相邻时间间隔变化的连续性越强，序列的变异越弱。

         在真实的交通网络中，一些交通事故或交通管制措施也会引起交通状态的突然变化。此外，传感器引起的噪音也会导致这种情况

        交通数据在时间维度上具有连续性的特点。

        因此，对于足够封闭的V的成对相邻列和(2≤j≤n)，假设j−1和j时间点的原始数据 相似。 即，成立，那么或者趋近于0

        推导过程如下：

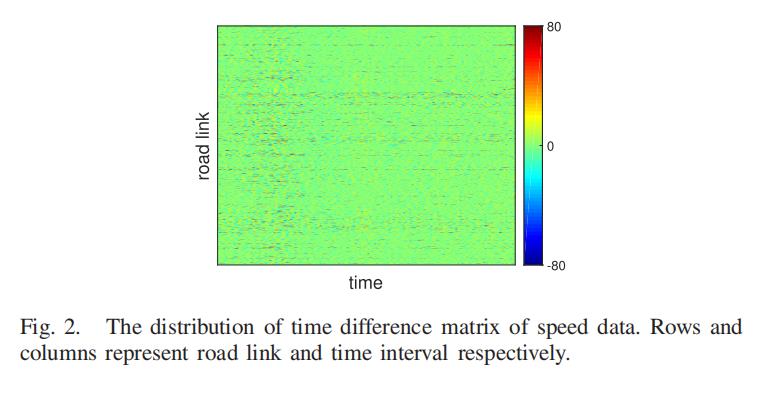
        图 2 显示了速度数据的时间差分矩阵的分布。 结果表明，大部分数据点在0附近浮动，只有少数数据点的幅度较大，这表明时差矩阵具有稀疏性。

        

        由于 l1 范数比 l2 范数 [20] 对噪声更稳健，我们通过 l1 范数计算 V 中每个条目的差异，即，重新表述目标问题 (8) 如下：  

        

        正则化项表示数据时间变化约束（也就是每一项的绝对值之和）

        T 是时间约束矩阵 T = Toeplitz(0, 1, −1)

        

        这种时间约束直观地表达了这样一个事实，即相邻时间点的流量数据在存在突变时通常也是相似的。

 

        比如此时V是一个m×n的矩阵

        那么，也就是相邻时间点各观测值之间的差距

        就相当于式相邻时间点各观测值之间的差距的绝对值之和

        4.2 自适应空间邻域相似度

        如前所述，因子矩阵U反映了路段的局部静态特征， 不同的空间点通过路网拓扑连接在一起。 大规模路网拓扑的高度复杂性以及原始矩阵的数据丢失使我们无法直观地找到空间约束关系，即类似于上述形式的简单矩阵是不合适的。

        尽管低秩方法通过利用局部空间相似性为数据补全提供了一种有效的方法，但由于它没有利用原始数据中存在的各种不确定噪声干扰，因此对于现实世界的交通通常无法获得令人满意的补全结果。 因此，我们寻求一种通过自适应地定位具有相似模式的局部邻域来重建丢失对象的方法。 然后使用邻域来表示目标道路链接数据。 这样可以同时满足全局低秩特征。

        最近，在无监督聚类领域，许多研究人员开发了基于拉普拉斯正则化的子空间聚类方法[21]、[22]。

        Laplacian 正则化器的思想来源于图论 [23]，其中为数据 构建无向局部 k 连通图，并由对称亲和矩阵编码，其中 0 ≤ aij ≤ 1 反映了数据点 yi 和 yj 连通的概率，即如果 aij > 0，则 yi 和 yj 在局部邻域中。

        因此，这些数据点的局部几何可以相应地反映在数据表示矩阵 X 中 以下：

        

TAS-LR 论文辅助笔记 & 图拉普拉斯正则项推导_UQI-LIUWJ的博客-CSDN博客

 是拉普拉斯矩阵

D是度矩阵

         Laplacian 正则化器旨在通过基于局部连通性为数据点自适应地分配邻居来学习亲和矩阵，其中即使存在噪声和缺失数据，亲和矩阵也是基于原始数据构建的 [24]-[26] .

        受其数据表示机制的启发，我们扩展了亲和力矩阵以找到道路网络子空间。

         因此，我们可以这么假设：如果空间点数据与其最优空间邻域空间点数据有较小的距离，那么它们有较高的相似性。（越近的越像）我们基于这个假设，构建一个有意义的亲和度矩阵A。

        在我们的模型中，亲和度矩阵 A 可以直接从数据样本的几何结构中计算出来。

        例如，可以使用 KNN 方法为每个样本选择 k 个最近邻，A 的元素 aij 可以通过 yi 与其近邻 y j 之间的欧几里德距离来设置。

         然而，这种构建亲和度矩阵的方法可能会被数据中的噪声或异常值破坏。

         如前所述，用固定拓扑测量数据相似性是片面的。

        U 反映了空间链接的静态特征，对于一组列，U = (u1, u2,..., um)，为了揭示道路数据之间的局部几何结构，我们采用了类似[ 26]的方法构建自适应亲和度矩阵如下：

        

        表示全1的m维向量。

         是为了 约束概率

        然而，简单地解决问题（11）会导致只有最近的aij（或同样最近的数据）被分配为概率 1 ，而所有其他表示的概率为 0。

        为了避免这种平凡解 ，我们选择 l2 范数 来解决这个问题

        将关注点与轻微的代数变换放在一起，f (·) 给出了以下约束：

        

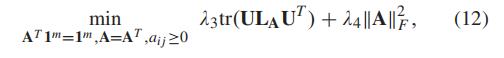
        结合上述时间约束，最终优化问题转化为以下公式：

        

        我们将模型称为时间和自适应空间约束低秩 (TAS-LR) 方法。 通过上述约束，我们可以自适应地选择与目标链路最相似且具有相同道路等级、车道数或容量特征的 k 个链路。

        这克服了传统方法通过预先粗略解释缺失数据来计算相似度的缺点。

4.2.1 A的更新方式

在论文的附录里有这个亲和力矩阵A的更新方式

首先我们在得到一组U之后，可以用此时得到的U来计算两个点之间的两两距离

  

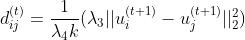
 表示第t+1 次迭代得到的U 的第i列

然后我们就可以用d来更新我们的A矩阵

这个是 ，是把d矩阵逐列从小到大排序

 表示如果元素为负数，那么我们就将其设置为0

 但此时算出来的矩阵不是对称矩阵，所以我们：

 

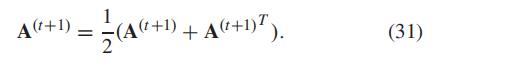
4.3 模型汇总

 汇总一下

 然后使用拉格朗日算子：

其中

其中G1,G2,G3是拉格朗日乘子

于是算法有： 

 

 

5 实验部分

5.1 数据集

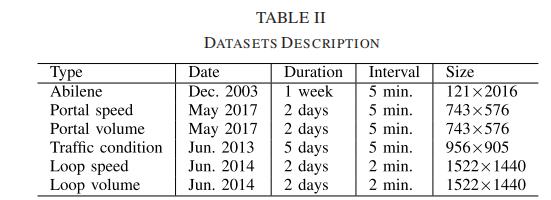
        六种不同类型的实际交通数据用于评估我们方法的完井性能，这些数据的特性总结在表 II 中。

        1) Abilene ：Abilene 数据以前用于各种研究 [28]、[29]，并根据 Abilene 网络上的起点-终点流量的测量记录汇总流量数据，该网络涵盖 121 个起点-终点对。

         2）portal数据：portal数据[30]记录了波特兰-温哥华大都市区高速公路的5分钟粒度速度数据和体积数据，环路线圈检测器覆盖了743条道路连接。

        3) traffic condtion数据：路况数据记录了北京三环高速路段内装有GPS的浮动车采集的平均通行速度数据。

        4) Loop Detector Data：环路线圈检测器采集的一种交通状况数据，涵盖北京五环高速公路内的道路平均车速和流量数据。

        为了分析这些数据集在时间轴上的变化特征，给出了增量率（简称roi）的定义。 

        

         

        根据（16）计算相邻时间片上每个交通数据集对的roi，然后拟合这些roi的累积密度分布（cdf）。

 

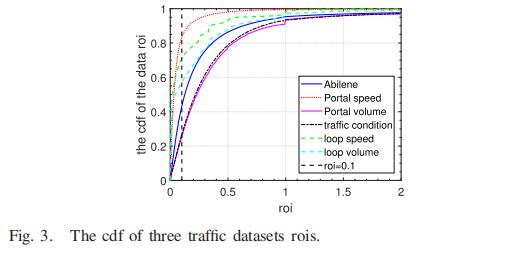
        图3为六个数据集的cdf曲线结果，roi的cdf随着roi的增加而上升到1，超过90%的数据，它们的rois在0到2之间波动。

        当roi等于0.1时，Portal-speed数据roi的cdf比例大于0.8的比例最高，而traffic-condition数据的比例最低，小于0.3，这说明Portal速度数据的变化率低于交通状况数据。显然，高速公路速度数据的连续性由于其可访问性低而相对较好，而城市网络数据由于更复杂的干扰而发生变异的概率较高。

         而且，注意到Portal速度数据rois的cdf高于Portal 流量的数据，loop 速度数据rois的cdf高于loop 流量的数据。因此我们推测流量数据相对于速度数据的变化特征更不稳定 . 上述分析符合我们模型的时间假设。

 5.2 实验配置

5.2.1 准确度衡量      

  准确度衡量：我们使用归一化平均绝对误差 (NMAE) 来衡量准确度，同时也是用RM

SE来衡量准确度 

5.2.2 U,V矩阵的秩

        r ≤ min m, n 反映了矩阵的全局低秩结构和特征分量的维数。

        低秩约束是强约束，对重构性能最敏感。 潜在矩阵的维数通常显着低于实际数据的维度 。

         通常，不同的数据具有不同的 r 最佳值。

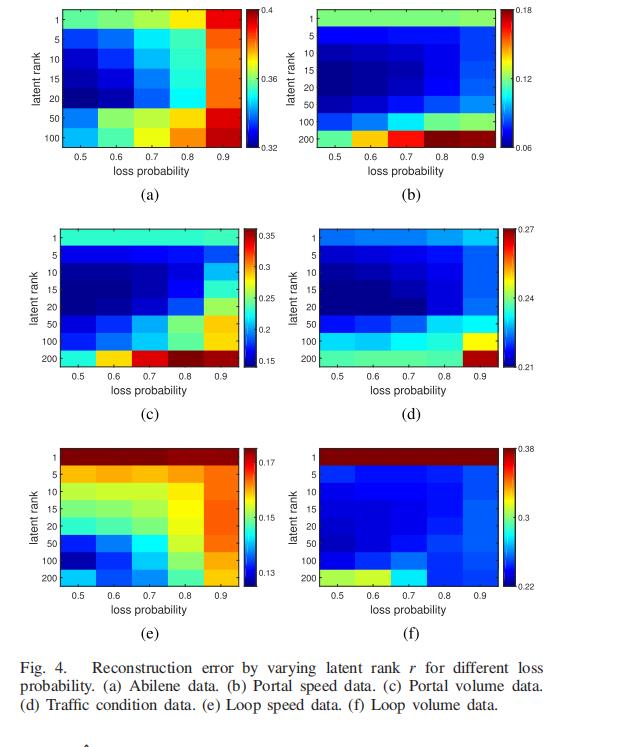
        图 4 显示了通过将 r 的损失率从 50% 变化到 90% 的情况下，在六个数据集上重建性能的变化。

        可以发现，所有数据的重构误差，当潜在矩阵秩较小的时候，具有相对较低的值，而在潜在矩阵秩较高时，具有相对较大的值。

         这意味着更高的潜在矩阵秩可能会产生很多冗余信息。（当然潜在矩阵秩太少了就不能很好地学习到所有的特征）

         对于前四个数据集，当 r 等于 20 时，它们的误差往往最低。

        对于loop速度和容量数据，最优秩可能会稍大一些，因为其空间维数相对较大，网络结构更复杂。

       

5.2.3 邻居数量

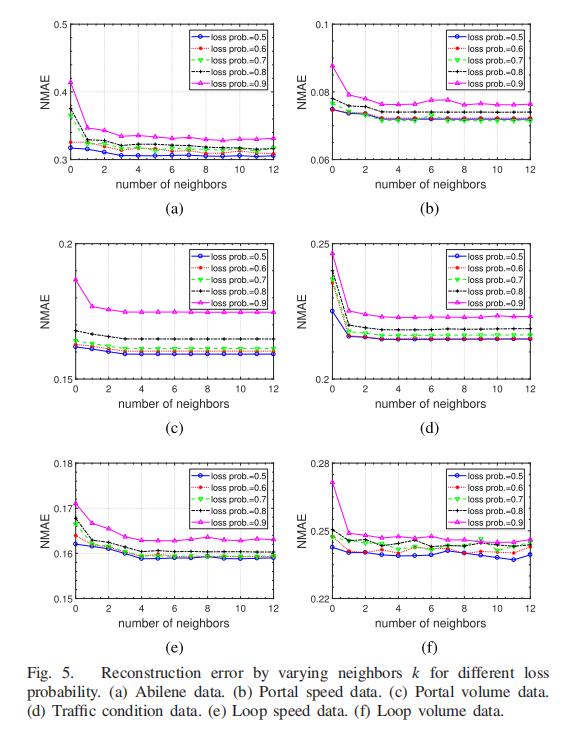
        k 表示空间关系中相似邻居的数量。 我们研究了所有数据集的变化 k 的影响，如图 5 所示。结果表明，随着 k 的增加，所有数据集的数据重构误差都减小了。

        k=4后，误差保持相对稳定。 因此，在我们的实验中，我们为所有数据集选择 k = 4。

        

5.2.4 正则化参数

        

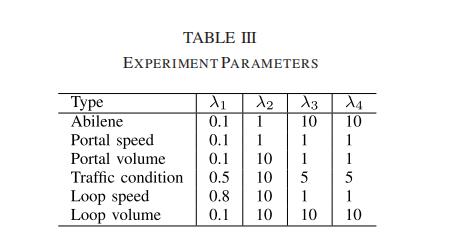
        λ1、λ2、λ3和λ4分别是对应于低秩项、时间约束项和空间约束项的非负权重。

        我们根据经验和实验选择这些参数。

        一般来说，秩约束项的值大于时间约束项的值，因此λ2通常大于λ1。

        此外，时间约束项和空间约束项的权重通常很接近。

        与此同时，鉴于是为了便于模型的求解，它对重构误差的敏感性较低。 我们可以设置 λ4 和 λ3 相等。

5.2.5 时间特征矩阵分析

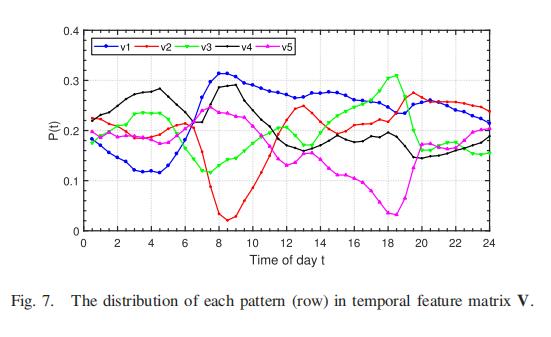
        图 7 描绘了速度数据的五个维度的时序情况（V 中的五行）。

        P(t) 表示在时间 t 时每个维度的比例。 P(t)越低，速度贡献越小，越容易造成堵塞。

        第一个时间分量 v1，其速度贡献在晚上 0-6 点最低，在白天几乎最大。可以推断出结果是夜间工作的车流造成的。

        第二个时间分量 v2 反映了典型的早高峰模式，在上午 7-10 点之间贡献最小。

         v4 主要分布在下午，反映了上午 12 点之后的交通流量。

        最后一个分量 v5 代表典型的夜间高峰模式，因为路网在下午 6 点达到最大拥堵。

5.2.6 空间特征矩阵分析

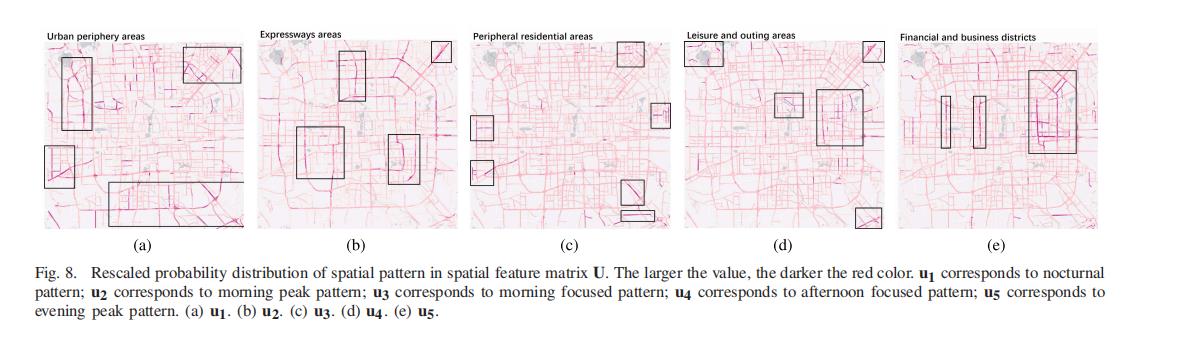
        图 8 显示了 U 中每个空间模式的分布，黑框标记的位置代表显着区域。 每行中的值重新调整为0-1，值越高，道路连接的特征越显着。 结合图7，我们在图8中解释了以下细节：

        

• 夜间模式：在图8（a）中，显着区域集中在城市外围地区，例如 南四环高速公路及与之相连的主干道，东北三元桥附近区域等。我们从图7中可知，该空间分布对应夜间交通流量，v1，因此可以推断 这种空间格局分布是由夜间出入市中心的交通流量造成的
• 早高峰模式：在图8（b）中，突出区域主要分布在高速公路区域，这与早高峰时段的通勤行为导致的交通拥堵区域一致（参见图7中v2的说明）。
• 晚高峰模式：再看图8（e），突出区域位于金融和商业区，例如 东二环和三环，西二环附近。 这些地方正是通勤者众多的主要中央商务区 (CBD) 或金融区。 交通流量会在晚高峰时段从这些地方扩散，导致区域拥堵（低速），这与图 7 中 v5 的解释一致。
• 晨间集中模式：图8(c)中，虽然突出区域不那么明显，但可以看出它们主要位于外围居民区。 图 7 表明该类交通是对应于 v3 的早晨集中活动，其高峰时间早于 v2，因此我们可以推断它是一些长距离的早晨交通流。
• 下午集中模式：图8(d)中标注的重点区域包括颐和园周边区域、什刹湖、CBD、机场高速等。显然，这些区域是休闲和郊游区域，因此出行时间主要集中在 下午，这与图 7 中 v4 暗示的时间特征一致

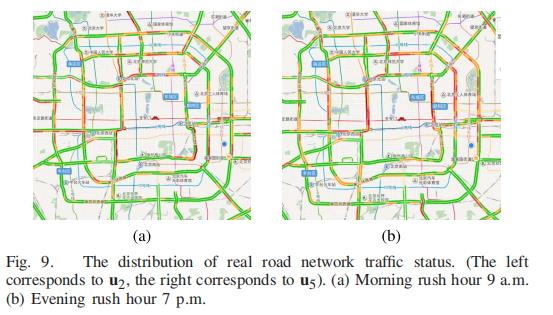
        我们还在图 9 中展示了路网交通的实际状态。它表明早高峰和晚高峰的拥堵路段与我们对特征矩阵的分析是一致的。

         基于上述分析，分解后的潜在矩阵分别反映了交通数据的时间和空间隐藏的低维模式，可以看作是一个特征提取过程。

        因此，我们可以通过分别对潜在空间矩阵和时间矩阵施加约束来实现有效的数据重建。