因子分析(R实例)
Posted Yeexxxx___
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了因子分析(R实例)相关的知识,希望对你有一定的参考价值。
本次实验使用的数据也是主成分分析实例的学生成绩数据. pca
data=read.csv("score.csv",header=T)
cor(data)
source("msaR.R") # 调用自定义函数 (放在最后了)
fac0=msa.fa(data,2,rotation="none") # 主成分法,且不做因子旋转
fac0
# 简单验证一下结果里都是什么
a = eigen(cor(scale(data))) # 相关系数矩阵的特征值、特征向量
a$values[1:2] # 前两个特征值
sum((sqrt(3.71)*a$vectors[,1])**2) # 载荷矩阵列平方和
(sqrt(3.71)*0.4121)**2+(sqrt(1.262)*(-0.376))**2 # 行平方和=共同度
sqrt(3.71)*a$vectors[,1] # 载荷矩阵第一列 sqrt(特征值)*特征向量
factanal(data,factors=2,rotation="none") # 极大似然法 不做因子旋转
fac1=msa.fa(data,2,rotation="varimax") # 用主成分法采用方差最大化作因子正交旋转
fac1
plot(fac1$loadings,xlab="Factor1",ylab="Factor2") # 因子载荷图
rnames=c("数学", "物理", "化学", "语文", "历史", "英语")
text(fac1$loadings[,1],fac1$loadings[,2],labels = rnames, adj=c(0.5, -0.5))
biplot(fac2$scores,fac2$loadings) #画出各个学生的因子得分图和原坐标在因子的方向,全面反映了因子与原始数据的关系
样本相关系数矩阵:

根据样本的相关系数矩阵可以粗略的认为保留两个因子.
主成分法估计载荷矩阵:


极大似然法估计载荷矩阵:

从上述极大似然法和主成分法得出的结果可以看出,极大似然法前两个因子的累积贡献率为74.5%,而主成分分析法的累计贡献率则达到了82.87%,说明主成分法效果比极大似然法好. 原因在于,实际数据大多数很难服从多元正态分布的要求,而极大似然法做因子分析要求数据样本服从多元正态分布.
为了使结果的结构更简单,更容易解释,所以对因子进行正交旋转,结果如下:

语文(
x
4
x_4
x4)、历史(
x
5
x_5
x5)、英语(
x
6
x_6
x6)在第一个因子的载荷分别为0.8763,0.9174,0.9253,这三个指标都反应了学生的文科水平,所以我们将其命名为“文科因子”;数学(
x
1
x_1
x1)、物理(
x
2
x_2
x2)、化学(
x
3
x_3
x3)、在第二个因子的载荷分别为0.8390,0.7837,0.8967,这三个指标则反应了学生的理科水平,所以我们将其命名为“理科因子”. 文科因子得分越高说明该学生文科成绩越好,理科因子得分越高说明该学生理科成绩越好.

从因子载荷图也可以看出,语文、英语、历史离第一个因子所代表的坐标轴近,数学、物理、化学则离第二个因子所代表的坐标轴近。因子旋转的作用就体现在这里,让载荷矩阵的列内方差最大,使得原始变量在因子空间可以离坐标轴更近. 这里做的是正交旋转,也就是坐标轴在旋转的过程中始终保持垂直,所以共同度是不会改变的。
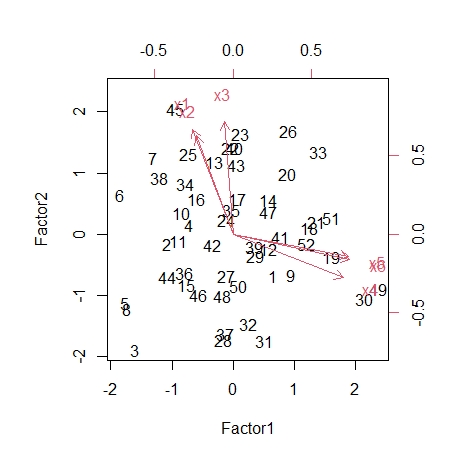
各个学生的因子得分图中可以看出33号同学的文科、理科因子得分都挺高,说明33号的文科理科成绩都好(均衡表现好,可以返回PCA看一下第二主成分的结果. pca);3号位于右下角,文科、理科因子得分都偏低,说明文、理成绩都不好;其他位于左上角和右下角的同学存在偏科的情况.
函数来自《多元统计分析及R语言建模》(王斌会编著,暨南大学出版社,2011年)
# msaR.R
options(digits=4)
#par(mar=c(4,4,2,1),cex=0.8) #鐠佸墽鐤嗛崶鎯ц埌鏉堝綊妾崪灞界摟娴f挸銇囩亸?
msa.X<-function(df)
X=df[,-1];
rownames(X)=df[,1];
X
msa.andrews<-function(x)
# x is a matrix or data frame of data
if (is.data.frame(x)==TRUE)
x<-as.matrix(x)
t<-seq(-pi, pi, pi/30)
m<-nrow(x); n<-ncol(x)
f<-array(0, c(m,length(t)))
for(i in 1:m)
f[i,]<-x[i,1]/sqrt(2)
for( j in 2:n)
if (j%%2==0)
f[i,]<-f[i,]+x[i,j]*sin(j/2*t)
else
f[i,]<-f[i,]+x[i,j]*cos(j%/%2*t)
#plot(c(-pi,pi), c(min(f),max(f)), type="n", xlab="t", ylab="f(t)")
plot(c(-pi,pi), c(min(f),max(f)), type="n", xlab="", ylab="")
for(i in 1:m) lines(t, f[i,] , col=i)
legend(2,max(f),rownames(x),col=1:nrow(x),lty=1:nrow(x),bty='n',cex=0.8)
msa.coef.sd<-function(fm)
b=fm$coef;b
si=apply(fm$model,2,sd);si
bs=b[-1]*si[-1]/si[1]
bs
msa.cor.test<-function(X,diag=TRUE)
p=ncol(X);
if(diag)
tp=matrix(1,p,p);
for(i in 1:p)
for(j in 1:i) tp[i,j]=cor.test(X[,i],X[,j])$stat;
for(j in i:p) tp[i,j]=cor.test(X[,i],X[,j])$p.value;
cat("corr test: \\n");
tp=round(matrix(tp,p,dimnames=list(names(X),names(X))),4)
print(tp)
#return(tp)
cat("lower is t value, upper is p value \\n")
else
cat("\\n corr test: t value, p value \\n");
if(is.matrix(X)) var=1:p
else var=names(X);
for(i in 1:(p-1))
for(j in (i+1):p)
cat(' ',var[i],'-',var[j],cor.test(X[,i],X[,j])$stat,cor.test(X[,i],X[,j])$p.value,"\\n")
msa.pca<-function(X,cor=FALSE,m=2,scores=TRUE,ranks=TRUE,sign=TRUE,plot=TRUE)
if(m<1) return
PC=princomp(X,cor=cor)
Vi=PC$sdev^2
Vari=data.frame('Variance'=Vi[1:m],'Proportion'=(Vi/sum(Vi))[1:m],
'Cumulative'=(cumsum(Vi)/sum(Vi))[1:m])
cat("\\n")
Loadi=as.matrix(PC$loadings[,1:m])
Compi=as.matrix(PC$scores[,1:m])
if(sign)
for (i in 1:m)
if(sum(Loadi[,i])<0)
Loadi[,i] = -Loadi[,i]
Compi[,i] = -Compi[,i]
pca<-NULL
pca$vars=Vari
if(m<=1) pca$loadings = data.frame(Comp1=Loadi)
else pca$loadings = Loadi;
if(scores & !ranks) pca$scores=round(Compi,4)
if(scores & plot)
plot(Compi);abline(h=0,v=0,lty=3)
text(Compi,row.names(X))
# par(mar=c(4,4,2,3))
# biplot(Compi,Loadi); abline(h=0,v=0,lty=3)
# par(mar=c(4,4,1,1))
if(scores & ranks)
pca$scores=round(Compi,4)
Wi=Vi[1:m];Wi
Comp=Compi%*%Wi/sum(Wi)
Rank=rank(-Comp)
pca$ranks=data.frame(Comp=round(Comp,4),Rank=Rank)
pca
msa.fa<-function(X,m=2,scores=TRUE,rotation="varimax",common=TRUE,ranks=TRUE)
if(m<1) return
cat("\\n")
S=cor(X);
p<-nrow(S); diag_S<-diag(S); sum_rank<-sum(diag_S)
rowname = names(X)
colname<-paste("Factor", 1:p, sep="")
A<-matrix(0, nrow=p, ncol=p, dimnames=list(rowname, colname))
eig<-eigen(S)
for (i in 1:p)
A[,i]<-sqrt(eig$values[i])*eig$vectors[,i]
for (i in 1:p) if(sum(A[,i])<0) A[,i] = -A[,i]
h<-diag(A%*%t(A))
rowname<-c("Variance","Proportion","Cumulative")
B<-matrix(0, nrow=3, ncol=p, dimnames=list(rowname, colname))
for (i in 1:p)
B[1,i]<-sum(A[,i]^2)
B[2,i]<-B[1,i]/sum_rank
B[3,i]<-sum(B[1,1:i])/sum_rank
W=B[2,1:m]*100;
Vars=data.frame('Variance'=B[1,],'Proportion'=B[2,]*100,
'Cumulative'=B[3,]*100)
A=A[,1:m]
if(rotation == "varimax" & m>1)
#cat("\\n Factor Analysis for Princomp in Varimax: \\n\\n");
VA=varimax(A); A=VA$loadings;
s2=apply(A^2,2,sum);
k=rank(-s2); s2=s2[k];
W=s2/sum(B[1,])*100;
Vars=data.frame('Variance'=s2,'Proportion'=W,'Cumulative'=cumsum(W))
rownames(Vars) <- paste("Factor", 1:m, sep="")
A=A[,k]
for (i in 1:m) if(sum(A[,i])<0) A[,i] = -A[,i]
A=A[,1:m];
colnames(A) <- paste("Factor", 1:m, sep="")
fit<-NULL
fit$vars<-round(Vars[1:m,],3)
if(m<=1) fit$loadings <- data.frame("Factor1"=round(A,4))
else fit$loadings <- round(A,4)
if(common)
fit$common <- round(apply(A^2,1,sum),4)
Z=as.matrix(scale(X));
PCs=Z%*%solve(S)%*%A
fit$scores <- round(PCs,4)
if(ranks)
W=apply(fit$loadings^2,2,sum)
Wi=W/sum(W);
F=PCs%*%Wi
fit$ranks=data.frame(Factor=round(F,4),Rank=rank(-F))
fit
msa.KMO<-function(r)
cl <- match.call()
if (nrow(r) > ncol(r))
r <- cor(r, use = "pairwise")
Q <- try(solve(r))
if 以上是关于因子分析(R实例)的主要内容,如果未能解决你的问题,请参考以下文章
R语言主成分分析PCA和因子分析EFA主成分(因子)个数主成分(因子)得分主成分(因子)旋转(正交旋转斜交旋转)主成分(因子)解释
R语言因子分析FA(factor analysis)实战案例