人工智能导论期末复习合集

Posted 2022-01-22 显然易证

人工智能导论期末复习合集

---

AI导论知识点目录

• 人工智能导论期末复习合集
• 〇、绪论
• 一、知识的概念
• • 练习题
• 二、基本搜索
• • 2.1 状态空间法
  • 2.2 无信息搜索
  • • 2.2.1 宽度优先搜索【队列】
    • 2.2.2 深度优先搜索【栈】
    • 2.2.3 一致代价搜索【优先队列】
    • 练习题
  • 2.3 启发式搜索
  • • 2.3.1 贪婪搜索【优先队列】
    • 2.3.2 A*搜索【优先队列】
    • 总结
    • 练习题
• 三、约束满足问题
• • 3.1 回溯法
  • 3.2 排序策略
  • • 3.2.1 最少可取值
    • 3.2.2 度启发式
    • 3.2.3 最少约束值
  • 3.3 推理策略
  • • 3.3.1 约束传播-局部相容性
    • 3.3.2 智能回溯
    • 3.3.3 前向检查
  • 3.4 问题结构特性
  • • 3.4.1 树状约束满足问题-图转树
    • 练习题
  • 3.5 局部搜索
  • • 3.5.1 爬山法
    • • 改进爬山法
    • 3.5.2 模拟退火
    • 3.5.3 局部束搜索
    • 3.5.4 遗传算法
    • 练习题
• 四、对抗搜索
• • 4.1 Minimax
  • 4.2 Alpha-Beta剪枝
  • 4.3 优化
  • 练习题
• 五、贝叶斯推理
• • 5.1 推理（参考离散数学）
  • 5.2 贝叶斯推理（概率论与数理统计回顾）
  • 练习题
• 六、专家系统
• • 6.1 基本概念
  • 练习题
• 七、机器学习
• • 7.1 机器学习概述
  • 7.2 相关问题
  • 7.3 研究内容
  • • 有监督学习
    • 无监督学习
    • 半监督学习
    • 研究内容
  • 7.4 基本概念
  • • 假设空间
    • 模型评估与选择
    • 数据集的划分
    • 性能度量
  • 练习题
• 八、维度约简
• • 8.1 概述
  • 8.2 特征选择(不考)
  • • 过滤式
    • 包裹式
    • 嵌入式
  • 8.3 互信息特征选择
  • 练习题
• 九、深度学习绪论
• • 9.1 神经网络基础
  • 9.2 经典神经网络
  • 9.3 卷积神经网络
• 十、集成学习
• • 10.1 集成学习基础
  • 10.2 个体生成
  • • 集成学习主要问题
    • 个体生成
• AI导论总结

---

〇、绪论

重点：人工智能定义、人工智能研究内容（了解、理解即可）

---

一、知识的概念

重点：知识的概念、知识的表示

知识是人们在长期的生活及社会实践中、在科学研究及实验中积累起来的对客观世界的认识与经验。
知识的形式：事实、因果关联
知识的特性：相对正确性（明确前提）、不确定性（真假之外）、可表示性（形式描述）、可利用性（学以致用）

练习题

• 知识的概念
  

---

二、基本搜索

2.1 状态空间法

· 状态：表示问题解法中每一步问题状况的数据结构
· 操作：状态变换的手段
· 状态空间：表示问题全部可能状态及其关系的图
· 状态空间的解：从初始状态到目标状态的操作算子序列

---

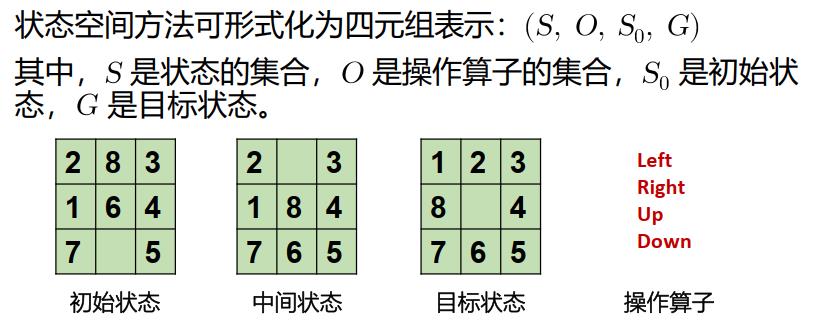
2.2 无信息搜索

只按预定的控制策略进行搜索,在搜索过程中获得的中间信息不会用来改进控制策略。

每个节点的分支数为b，最浅解位于第s层，搜索空间共m层。

2.2.1 宽度优先搜索【队列】

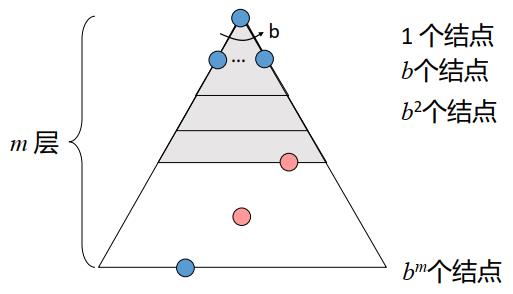
时间复杂度：O($b^s$)
空间复杂度：O($b^s$)
具有完备性、最优性

2.2.2 深度优先搜索【栈】

时间复杂度：O($b^m$)
空间复杂度：O($bm$)
可能不具有完备性（图有环时需进行约束）、不具有最优性（最左的解）

2.2.3 一致代价搜索【优先队列】

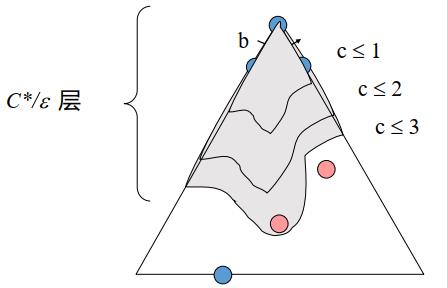
解代价为$C^{\ast }$，边最小代价为$\epsilon$

时间复杂度：O($b^{C^{\ast }/\epsilon }$)
空间复杂度：O($b^{C^{\ast }/\epsilon }$)
具有完备性、最优性

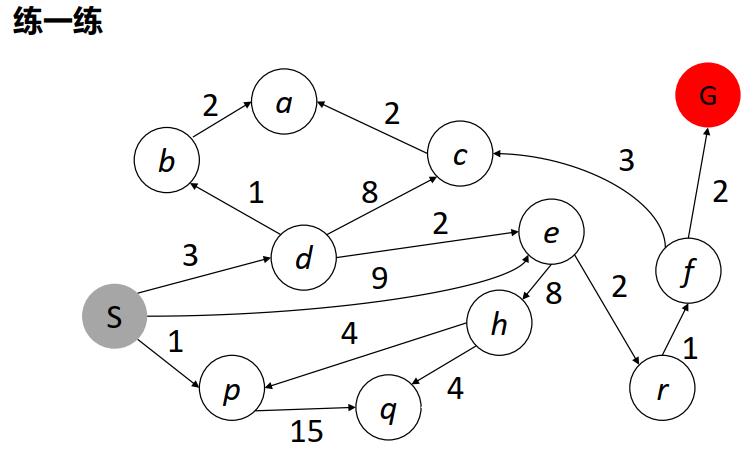
练习题

• 一致代价搜索的终止条件：

---

• 无信息搜索

---

2.3 启发式搜索

在搜索中加入了与问题有关的启发性信息，用于指导搜索朝着最有希望的方向进行，加速问题的求解过程并找到最优解。

2.3.1 贪婪搜索【优先队列】

搜索策略： 拓展看起来离目标最近的节点
评估函数： $f(n)=h(n)$【$h(n)$表示从$n$节点到目标节点最佳路径的估计代价】

最坏情况下退化为DFS，时间复杂度为O($b^m$)
空间复杂度：O($b^m$)【存储所有节点的信息】
不具有完备性和最优性

2.3.2 A*搜索【优先队列】

搜索策略： 避免拓展耗费已经很大的路径
评估函数： $f(n)=g(n)+h(n)$【g(n)表示初始节点到n节点的实际代价、h(n)表示估计代价】

• 可纳性
  如果对任意节点$n$, $h(n)\le h^{\ast }(n)$成立, 则启发式函数是可纳的(admissible), 其中， $h^{\ast }(n)$是结点$n$到目标状态的真实代价。

定理：若$h(n)$可纳，则A*搜索算法具有最优性。

• 一致性（一致->可纳）
  若对于任意节点$n$和通过操作$a$生成的后续节点$n^{\prime }$，则$h(n)\le cost(n,a,n^{\prime })+h(n^{\prime })$成立，则启发式函数是一致的

定理：若$h(n)$一致，则A*搜索算法具有最优性。

• 优势性
  对于任意节点$n$，可纳启发式函数$h_1(n)<h_2(n)$ ，称$h_2$优于$h_1$

• 最优性
  假设A是最优目标节点，B是次优节点，则A比B更早被搜索。
  

• A*算法性能分析
  $b$表示每个节点的后继节点数，$d$表示解的深度，$\epsilon$表示相对误差$\frac{h^{\ast }-h}{h^{\ast }}$ ，$h^{\ast }$为真实代价，$h$为估计代价

最坏时间复杂度：O($b^{\epsilon d}$)
空间复杂度：O($b^m$) -存储所有节点的信息

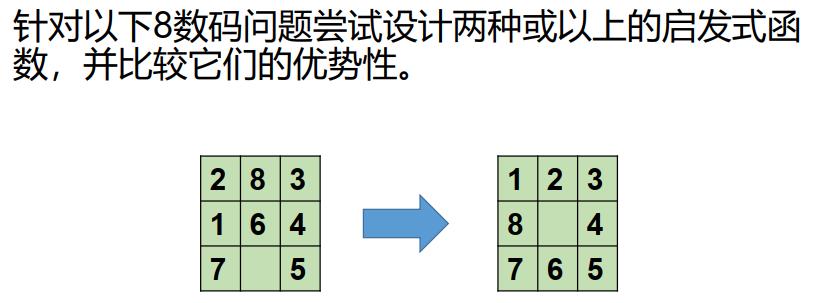
启发式函数设计

• 问题松弛化
  八数码问题：棋子可以从方格A->方格B，如果A与B水平或竖直相邻且B为空。
  去掉相关条件，形成松弛问题：

A与B相邻，棋子可从A移到B（距离）
如果B空，棋子可从A移动B
棋子可从A移动到B（不在位）

• 子问题分解
  原问题分解为多个子问题，考虑子问题的解代价。

• 模式数据库
  存储子问题模式解代价，从目标反向搜索计算模式代价，针对子问题，查找模式数据库。

• 从经验中学习

总结

1. A * 算法综合了后向路径代价和前向估计代价；
2. 如果启发式函数可纳/一致， A*是最优的；
3. 启发式函数设计是关键，应选具有优势的启发式函数。

练习题

• A*搜索
  

---

• 修道士问题（M-C问题）
  

---

• 各种搜索算法的搜索过程

---

---

三、约束满足问题

3.1 回溯法

以N皇后问题为例，从初始状态开始，按行逐一摆放皇后，遇到矛盾时返回上一状态，重新摆放皇后。
由此，搜索空间是一棵搜索树，直至搜索至第N层即可找到可行解。
回溯搜素 = DFS + 变量分配【每次一个变量】 + 约束检查【考虑与前面分配不冲突的变量值】

具有完备性
具有最优性
时间复杂度：O(N!)
空间复杂度：O(N)

---

3.2 排序策略

3.2.1 最少可取值

（对节点排序，每次选择值域最少可取值的变量）

3.2.2 度启发式

（对节点排序，每次选择度最大的变量）

3.2.3 最少约束值

（对颜色排序，选择给近邻变量留下更多选择的值）

---

3.3 推理策略

3.3.1 约束传播-局部相容性

• 节点相容（单个变量值域的所有取值满足其一元约束）
• 边相容（满足所有的二元约束）
  • 若X去除某个值，X的近邻需要再次检查，边相容比前向检查更早检测出错误
• 路径相容（通过观察变量得到隐式约束来加强二元约束）
• …k阶相容
• 强k阶相容（k-1,k-2,…,1也相容，无需回溯就可求解问题）

3.3.2 智能回溯

• 搜索失败时返回前一个变量，尝试另一个值，回溯到哪个变量？
  

3.3.3 前向检查

---

3.4 问题结构特性

极端情况：大问题由独立子问题构成，独立子问题可认为是约束图的连接组件（连通子图）

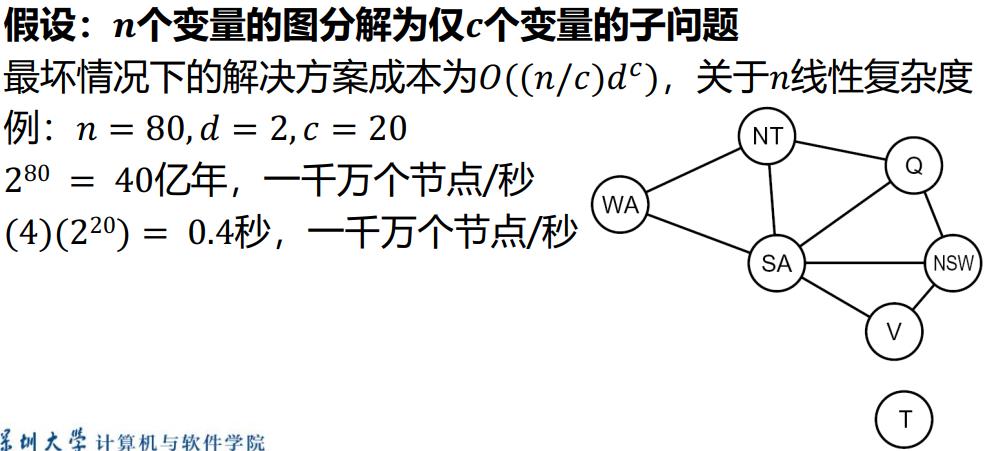
3.4.1 树状约束满足问题-图转树

• 变量（拓扑排序）：
  选择一个根变量，对变量进行排序，先父母后孩子。
  
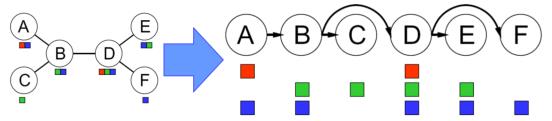
  两变量最多有一条路径，所以n个结点的树有n-1条边。

• 边相容：
  应用Remove Inconsistent（Parent($X_i$)，$X_i$）

• 变量分配：
  对于$i=1:n$，相容地分配$X_i$

练习题

---

3.5 局部搜索

优点

• 通常只用常熟级的内存
• 通常能在标准约束满足算法不适用的很大或无限的（连续的）状态空间中找到合理的解
• 对于解决纯粹的最优化问题十分有用，其目标是根据目标函数找到最佳状态
• 如果存在解， 最优的局部搜索算法可找到全局最大/最小值

CSP局部搜索

• 初始变量分配违反一些约束
• 重新分配变量值

基本思想
变量选择：随机选择任何有冲突的变量
值选择：最小冲突启发式

• 选择一个违反最少约束的值
• 爬山法——启发式信息h(n)=违反约束的总数
• 其他局部搜索方法：模拟退火、局部束搜索

3.5.1 爬山法

从任意初始状态开始，每次移动到最好的近邻状态，若无近邻状态比当前更好，则退出循环，得到爬山法的解。

1. 不具有完备性
2. 不具有最优性
3. 时间复杂度较低
4. 空间复杂度：O(N)

• 可从任意地方开始
• 重复：移动到最好的近邻状态
• 若无近邻状态比当前更好，则退出
  

无最优性的概念，不具有完备性。
特点：速度快，但易于陷入局部最优。

改进爬山法

• 随机爬山法：概率随机选择下一步，可能找到更好的解
• 首选爬山法：随机直至选到优于当前的结点，后继多时较好
• 随机重启爬山法：多次尝试，算法完备性的概率接近1

3.5.2 模拟退火

在爬山法的基础之上，允许“下山”动作跳出局部最优解，从而能有更大概率找到全局最优解。

1. 不具有完备性
2. 具有最优性
3. 时间复杂度比爬山法高
4. 空间复杂度：O(N)
   

3.5.3 局部束搜索

从k个随机生成的状态开始，每一步全部k个状态的所有后继被生成。如果其中有一个是目标状态，则算法停止；否则从整个所有后继列表中选择k个最佳后继，重复直至达到目标状态。

1. 不具有完备性
2. 不具有最优性
3. 时间复杂度比爬山法高
4. 空间复杂度：O(N)

（随机）束搜索：
在所有后继列表中随机选择k个后继，其中选中概率是状态值的递增函数，类似于自然选择。

3.5.4 遗传算法

遗传是随机束搜索的一个变形。把两个父状态结合（选择、交叉、变异）来生长后继，而不是通过修改单一状态进行。

1. 具有完备性
2. 具有最优性
3. 时间复杂度比爬山法高
4. 空间复杂度：O(N)

练习题

1. 回溯算法优化方法有哪些，其主要思想是什么，可以带来哪些好处？

2. 编程实现N皇后回溯搜索算法，至少采用一种优化策略加速搜索过程。

3. 实现N皇后至少一种局部搜索方法，并分析其算法的性能（四个搜索算法评价指标）。

---

四、对抗搜索

4.1 Minimax

搜索：自顶向下
计算：自底向上
搜索方法：类似DFS
时间复杂度：O($b^m$)
空间复杂度：O($bm$)
面临问题：搜索空间巨大

---

4.2 Alpha-Beta剪枝

一种找到最佳minimax步骤的方法，同时可以避免搜索不可能被选择的步骤的子树。
Alpha：可能步骤的最大下界
Beta：可能步骤的最小上界
任何新节点被认为是可能路径节点 当且仅当$\alpha \le Value(N)\le \beta$

剪枝性质：

• 剪枝不影响根节点Minimax值
• 中间节点值可能不同
• 子节点的次序影响剪枝效率
• 最好时间复杂度：O($b^{m/2}$)

软件工程导论期末复习试题集

计算机安全导论期末复习小笔记

网络空间安全导论期末复习资料

耗时一个月！期末熬夜复习整理 | 计算机网络（谢希仁第七版）大合集知识点+大量习题讲解

2022春山东大学人工智能导论期末题库附答案

人工智能及其应用（蔡自兴）期末复习