相机校正与相机内参外参

Posted 2022-01-22 卓晴

简 介： 对于相机进行校正，是为之后视觉测量奠定基础。本文在总结了相机校正中的基本概念。使用cv2的函数说明校正的过程。

关键词： 相机校正，内参，外参

 

§01 相机标定

---

  这部分内容来自于 python+OpenCV 相机标定 。

1.1 相机标定基本原理

  摄像机标定(Camera calibration)简单来说是从世界坐标系换到图像坐标系的过程，也就是求最终的投影矩阵 P 的过程。 根据相机标定（一）-原理及内参、外参 博文中的定义，在整个转换过程中，包括有四个坐标系：

• 图像像素坐标系
• 图像物理坐标系
• 相机坐标系
• 世界坐标系

  一般来说，标定的过程分为两个部分：

• 第一步是从世界坐标系转换为相机坐标系，这一步是三维点到三维点的转换，包括 $R,t$（相机外参）等参数；
• 第二部是从相机坐标系转为图像坐标系，这一步是三维点到二维点的转换，包括 $K$（相机内参）等参数；

1.1.1 世界坐标转换为相机坐标

  世界坐标就是实际外部环境坐标，原点为$O$，三个正交坐标轴分别为$X,Y,Z$。相机位于世界坐标内，$O_{X,Y,Z}$，原点为$C$，镜头方向坐标为$Z_{cam}$，另外两个坐标轴$X_{cam},Y_{cam}$与镜头方向垂直。

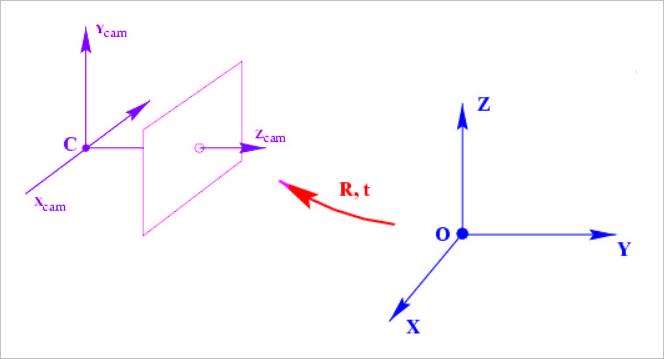
▲ 图1.1.1 世界坐标转换为相机坐标

  从$O_{X,Y,Z}$到$C_{Xcam,Ycam,Zcam}$的 映射转换公式为：$${\hat{X}}_{cam}=R\left(\hat{X}-\hat{C}\right)$$

其中：

• $R$表示旋转矩阵；
• $\hat{X}$表示$X$点在世界坐标$O_{X,Y,Z}$中的位置；
• $\hat{C}$表示相机原点$C$在世界坐标中的位置；
• ${\hat{X}}_{cam}$表示$X$点在相机坐标中的位置；

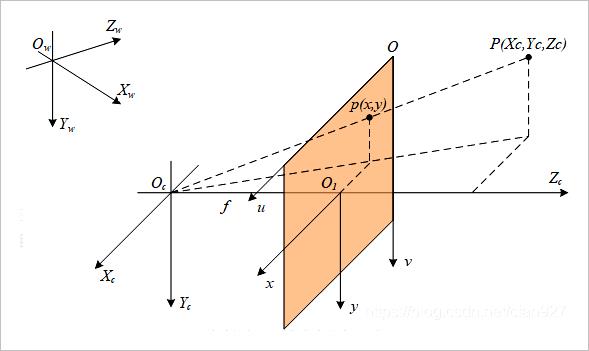
▲ 图1.1.2 世界坐标系与相机坐标系

1.1.2 相机坐标转换为图像坐标

  下图给出了在相机坐标系内的成像平面，$p_{x,y}$与相机坐标主轴垂直，交点为图像坐标原点$p$，距离相机与原点距离为相机焦距$f$。相机坐标中任何一点$X$在成像平面上的位置，也称为图像坐标，是由连线$X,C$在成像平面上的交点$x$确定。

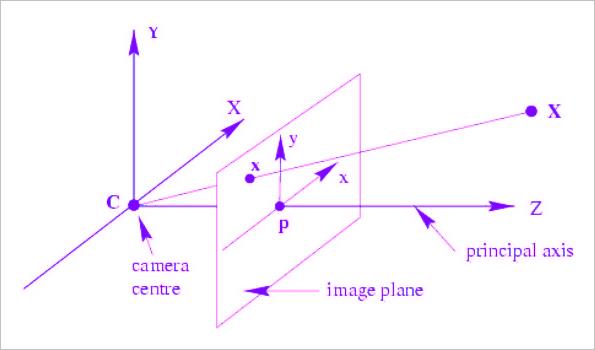
▲ 图1.1.3 相机坐标中的点与成像平面

其中：

• $C$表示 camera center，即相机的中心店，也是相机坐标系的原点；
• $Z$表示principal axis，即相机的主轴；
• $p$点所在的平面表示 image plane，即相机的像平面，也就是图片坐标系所在的二维平面；
• $p$ 点表示 principal point，即主点，也就是主轴与想平明香蕉的点；

  成像坐标$x$的位置可以由三角几何比例关系确定。

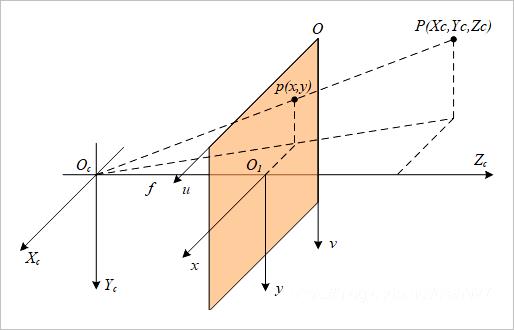
▲ 图1.1.4 相机坐标系以及成像平面之间的关系

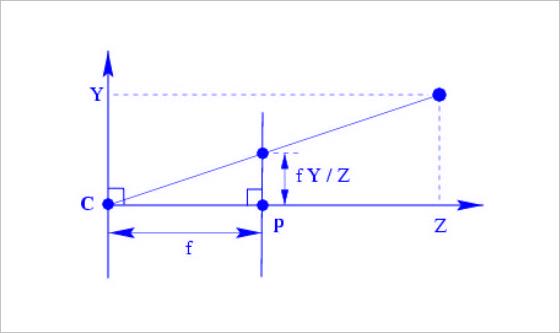
▲ 图1.1.5 利用三角几何比例关系确定成像位置

其中：

• $C$ 点到 $p$ 点的距离，就是相机的焦距 $f$；

  对于相机坐标中的点 $\left(X,Y,Z\right)$，在成像平面上的位置为：
$$x=\frac{f\cdot X}{Z},y=\frac{f\cdot Y}{Z}$$

  简记为：$\left(X,Y,Z\right)\mapsto \left(f\cdot X/Z,f\cdot Y/Z\right)$。

  加上偏移量，如下图所示， 其中 $p$是像平面坐标系的 原点，在图像坐标系中的位置为 ( p x , p y ) \\left( p_x ,p_y \\right) (p计算机视觉——相机内外参、相机标定

如何不用标定板来确定相机的外参矩阵

相机标定的内参、外参、畸变参数

内参外参畸变参数三种参数与相机的标定方法与相机坐标系的理解

Step1：模型 16个相机参数（内参外参畸变参数）

相机的内参外参标定