机器学习基础知识点

Posted 2022-01-21 陆嵩

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习基础知识点相关的知识，希望对你有一定的参考价值。

机器学习基础知识点

文章目录

机器学习基础知识点

机器学习主要分为监督学习和无监督学习。

有监督学习：对具有标记的训练样本进行学习，以尽可能对训练样本集外的数据进行分类预测。（LR、SVM、BP、RF、GBRT）
无监督学习：对未标记的样本进行训练学习，比发现这些样本中的结构知识。(KMeans、DL)

监督学习

回归

线性回归

所谓的线性回归，就是要找一个线性的超平面，去尽可能地拟合各个样本点。在一维的情况下，如图所示：

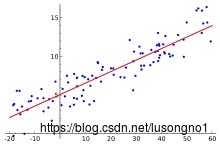
我们要寻找一条直线，让它尽可能地穿过这些点。“尽可能”可能有一些度量，比如说让误差平方和最小。
求解这条直线的方法有最小二乘方法等。
线性回归是一种简单但却使用的回归技术。

多重共线性（Multicollinearity）是指线性回归模型中的自变量之间由于存在高度相关关系而使模型的权重参数估计失真或难以估计准确的一种特性，多重是指一个自变量可能与多个其他自变量之间存在相关关系。共线性不影响模型的预测而是影响对模型的解释。神经网格本来可解释性就差，就不存在这种共线性的问题。

岭回归

lasso回归

分类

k最近邻分类

所谓物以类聚，人以群分，你的圈子基本决定了你的状态。我们可以用周围的邻居来判断自己的情况，基于这个思想，就有了k-NN算法。k近邻算法不仅可以用于分类，也可以用于回归，我这里将它放在了分类的条目下。

分类问题中，一个对象的分类是由其邻居的“多数表决”确定的，k个最近邻居（k为正整数，通常较小）中最常见的分类决定了赋予该对象的类别。若k=1，则该对象的类别直接由最近的一个节点赋予。无论是分类还是回归，衡量邻居的权重都非常有用，使较近邻居的权重比较远邻居的权重大。例如，一种常见的加权方案是给每个邻居权重赋值为1/d，其中d是到邻居的距离。这样会避免一些单纯计数带来的问题。

k 参数的选择可以使用交叉验证和自助法等等。

k-近邻算法的缺点是对数据的局部结构非常敏感。

三要素：

k 值的选择
距离的度量（常见的距离度量有欧式距离，马氏距离等）
分类决策规则（多数表决规则）

k 值的选择
k 值越小表明模型越复杂，更加容易过拟合。k 值越大，模型越简单，极端情况如果 k=N 的时候就表明无论什么点都是训练集中类别最多的那个类。所以一般 k 会取一个较小的值，然后用过交叉验证来确定。这里所谓的交叉验证就是将样本划分一部分出来为预测样本，比如 95% 训练，5% 预测，然后 k 分别取1，2，3，4，5之类的，进行预测，计算最后的分类误差，选择误差最小的 k。简单地来说，就是试一试。

KNN 的回归
在找到最近的 k 个实例之后，可以计算这 k 个实例的平均值作为预测值。或者还可以给这 k 个实例添加一个权重再求平均值，这个权重与度量距离成反比（距离越大，权重越低）。

优缺点：
KNN算法的优点：思想简单，理论成熟，既可以用来做分类也可以用来做回归；可用于非线性分类；训练时间复杂度为O(n)；准确度高，对数据没有假设，对 outlier 不敏感。
KNN算法的缺点：计算量大；样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）；需要大量的内存。

KNN 算法中 KD 树的应用
我们知道在上述 KNN 的计算中，我们要找一个点的 k 近邻，必须要计算这个点到所有点的距离，再取小的一部分。这个计算量超大。KD tree 就是为了解决这个问题的。顺着 KD tree 去搜索，我们可以很快地找到一个点的最近邻，而不需要计算这个点到所有点的距离。
当点随机分布的时候，搜索的复杂度为 $\\log(N)$ ，N 为实例的个数，KD 树更加适用于点的
数量远大于空间维度的 KNN 搜索，如果空间维度与点个数差不多时，它的效率基于等于线性扫描。
关于 KD 数的构建，搜索和 KNN 查找，网上有很多资料，这里就不介绍了。

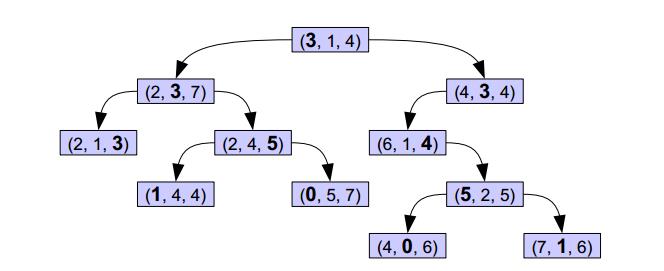
可以观察到 KD-tree 是这样一种 tree。它的第一层的第一个元素大于左子树的第一个元素，小于右子树的第一个元素。第二层的第二个元素大于左子树的第二个元素，小于右子树的第二个元素。第 i 层的第 i%k 个元素大于左子树的第 i%k 个元素，小于右子树的，依次类推。

朴素贝叶斯分类

朴素贝叶斯真的很朴素，用到的仅仅只是贝叶斯公式。以二分类为例，它给定若干组的带标签的数据，当新给一组特征时，我们需要判断它属于哪一类。

我们通过比较这组特征下的条件概率 $P(\\text标签1|\\\\text特征1，特征2，特征3\\)$ 和 $P(\\text标签2|\\\\text特征1，特征2，特征3\\)$ 大小来对其分类。条件概率的计算可通过贝叶斯公式来计算，即
$P(\\text标签i|\\\\text特征1，特征2，特征3\\) = \\fracP(\\\\text特征1，特征2，特征3\\|\\text标签i )* P(\\text标签i)P(\\\\text特征1，特征2，特征3\\)$

我们假设特征之间是独立的，那么就有
$\\beginaligned P(\\\\text特征1，特征2，特征3\\|\\text标签i ) &=& P(\\text特征1|\\text标签i )*P(\\text特征2|\\text标签i )*P(\\text特征3|\\text标签i ) \\\\ P(\\\\text特征1，特征2，特征3\\ ) &=& P(\\text特征1)*P(\\text特征2|\\text标签i )*P(\\text特征3 )\\endaligned$
这些量和**P(标签i)**都是可以通过统计已有的样本数据，用频率来概率得到。
注意要，使用朴素贝叶斯分类方法，我们假设了特征之间相互独立，看起来很有局限。事实上，我们在处理文本数据的时候，常常用到这种方法。

主要就是利用贝叶斯公式，把某组特征下产生某个标签的概率进行了拆解，进一步拆解是利用到了特征之间的不相关性。

基本过程如下：

假设现在有样本 $x=\\left(a_1, a_2, a_3, \\ldots a_n\\right)$ 这个待分类项 (并认为 $x$ 里面的特征独立)。
再假设现在有分类目标 $Y=\\left\\y_1, y_2, y_3, y_4 . . y_n\\right\\$ 。
那么 $\\max \\left\\P\\left(y_1 \\mid x\\right), P\\left(y_2 \\mid x\\right), P\\left(y_3 \\mid x\\right) \\ldots P\\left(y_n \\mid x\\right)\\right\\$ 就是最终的分类类别。
而根据贝叶斯公式 $P\\left(y_i \\mid x\\right)=\\fracP\\left(x \\mid y_i\\right) * P(y i)P(x)$ 。
因为 $x$ 对于每个分类目标来说都一样，所以不用管分子，就是求 $\\max \\left\\P\\left(x \\mid y_i\\right) * p\\left(y_i\\right)\\right\\$ 。
$P\\left(x \\mid y_i\\right) * P\\left(y_i\\right)=P\\left(y_i\\right) * \\prod\\limits_j=1^n\\left(P\\left(a_j \\mid y_i\\right)\\right)$
而具体的 $P\\left(a_j \\mid y_i\\right)$