自动驾驶 8-4: 最小二乘法和最大似然法 Least Squares and the Method of Maximum Likelihood

Posted 2022-01-19 AI架构师易筋

欢迎来到模块 1 的最后一课。 我们将通过以下方式完成模块 讨论一个重要的联系 将有助于提供进一步的直觉 对于最小二乘法。

具体来说，到本课结束时， 你将能够说明连接 最小二乘法之间 和最大似然估计 与高斯随机变量。

让我们从回忆开始 最小二乘准则来自 本模块中的第一个视频。

我们找到了最好的估计 一些未知但恒定的参数 确定使总和最小的值 基于我们测量的平方误差。

但我们可以问：为什么要平方误差？ 为什么不把错误立方， 或平方根错误，或其他什么？

这其实是一个特别深刻的问题， 并且有一整个领域 专门用于它的强大统计数据。

你确实可以使用不同的错误函数， 但我们将讨论两个原因 平方误差是有吸引力的和相关的。

1. 第一个很简单。 平方误差允许我们解决 最佳参数与 比较简单的代数。 如果测量模型是线性的， 最小化平方误差准则 相当于求解线性方程组。
2. 第二个原因与 概率和之间的深层联系 最小二乘和最大似然估计量 在高斯噪声的假设下。 你可能已经猜到了， 这种联系最初是派生的 以高斯的特定形式， 所以它涉及到也就不足为奇了 高斯随机变量或 相当于，高斯噪声。

要了解这种基本联系， 让我们首先讨论最大似然。 与其写下损失， 我们可以解决这个问题 最优参数估计 询问哪些参数使 我们记录的测量结果最有可能。

为了简单起见， 我们将坚持一个单一的标量参数 建立我们的直觉。

例如，让我们再看看测量电阻。 鉴于我们对概率的了解， 如果我们有四个可能的值 对于这个未知的电阻参数， X, x_a 到 x_d, 每一个都会引起 以下条件概率 在我们的测量 Y 上。

哪个值会最大化 给定测量值 y_meas? 的条件似然。 没错，x_a。

最高概率密度在 测量位置由下式给出 绿色曲线表示 x_a 是我们最可能的参数 给定这个测量值。

现在，如果我们采用简单的测量模型， 我们可以将其转换为概率密度 假设我们的附加噪声的密度。

未知参数 x 成为该密度的平均值， 方差就是我们的噪声方差。

回想一下，概率密度 一个高斯随机变量是 由以下等式给出。

这意味着我们可以表达 我们的测量似然 单次测量如下。

如果我们有多个独立的测量， 每个都具有相同的噪声方差， 我们可以简单地取 多个高斯导致另一个高斯。

我们可以尝试最大化这种可能性 相对于平均参数 x hat。

为此，我们将使用一种技术 常用于优化。 而不是直接最大化可能性， 我们将取其对数并将其最大化。

由于可能性总是一个正数， 因为对数是 单调递增函数， 这不会影响 最终结果非常方便。

一旦我们对这个可能性应用对数， 我们看到有东西弹出 看起来很像平方误差的总和。

此表达式中的常数 C 指的是 不是 x 和我们可以安全忽略的函数。 最后一步是现在 实现函数的argmax f 与 该函数的负数的 argmin。

利用这个事实，我们可以转 我们的似然最大化为 误差平方和的最小化。

瞧，最小化总和 平方误差等价于最大化 一组测量的可能性 假设测量值被加法破坏， 等方差的独立高斯噪声。

此外，如果我们保持相同的假设， 但改变方差 每次测量的高斯噪声， 我们可以达到相同的标准 我们在加权最小二乘法视频中看到。

所以在这两种情况下， 给定的最大似然估计 加性高斯噪声是 等价于最小二乘法或 我们之前推导出的加权最小二乘解。

那么为什么这个结果如此重要呢？ 一辆自动驾驶汽车将不得不处理许多问题， 许多错误来源， 其中一些非常难以建模。

然而，中心极限定理告诉我们 当将所有这些错误组合在一起时， 他们可以合理地建模为 单个高斯误差分布。

我们想对我们的系统进行概率建模 并保持计算的简单性。

如果我们的错误是高斯的， 那么最好的最大值 参数的似然估计 兴趣正是最小二乘解 我们已经熟悉了，简单。

最后，让我们讨论一下 这种方法的一个重要警告。

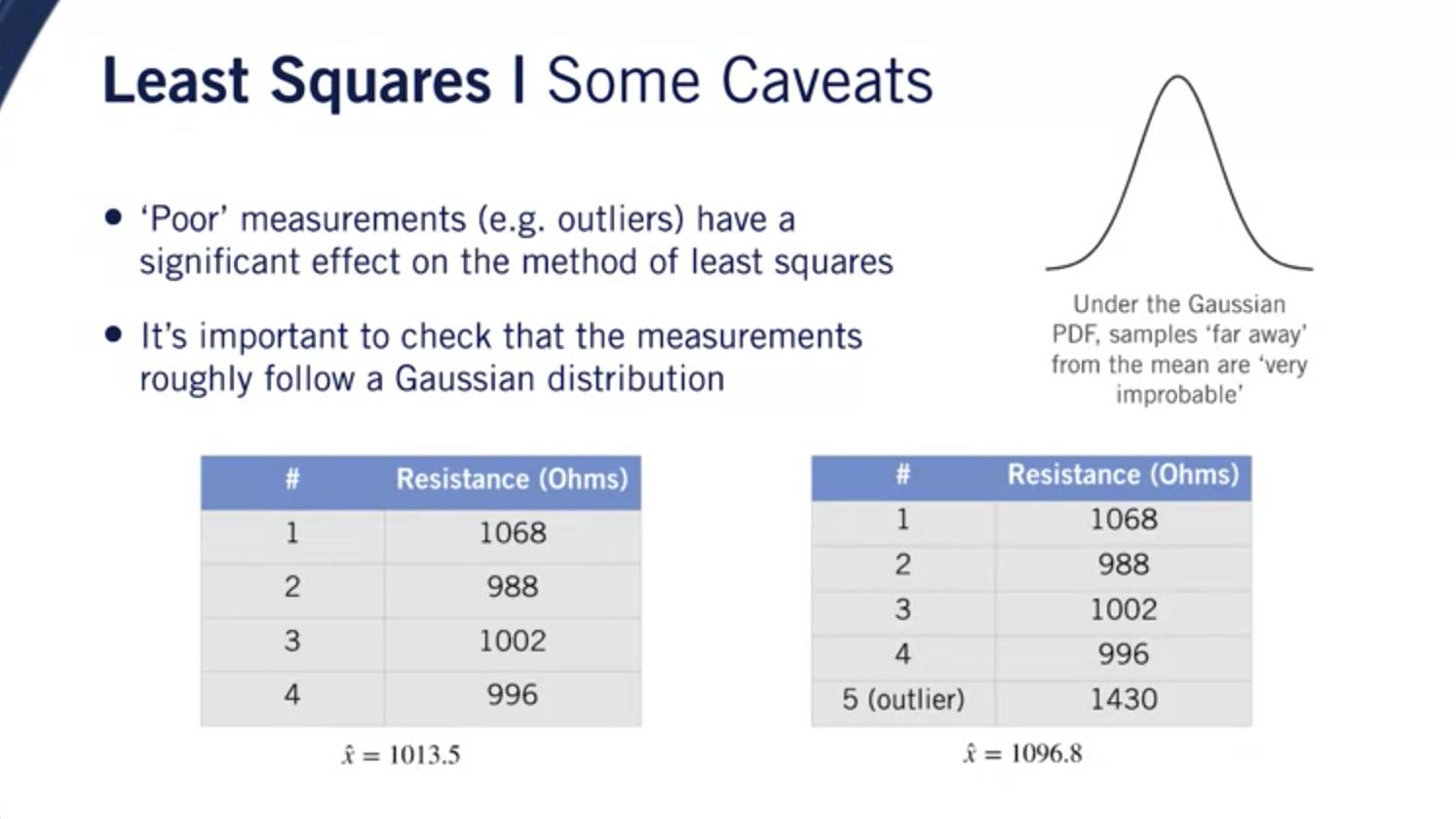
当我们使用最小二乘法时， 测量异常值可以有 对我们的最终估计有重大影响。

要了解原因， 考虑在高斯分布下， 距离两个标准差的样本 均值有 发生的概率小于百分之五。

结果，如果有 我们测量数据中的一些异常值， 最大似然法等价， 最小二乘法将把 这些测量具有重要意义。

所以估计值 我们的参数将被这些异常值强烈拉动。

我们的最优方法会出现偏差 以便更可能进行外围测量。

这可能发生在许多使用 来自自动驾驶汽车的传感器数据。

异常值可能来自于人 走在激光雷达扫描的中间， 例如，或者 GPS 信号不好。

考虑我们的电阻器示例。 用一个外围测量 这可能来自一个简单的事故， 最终估计被大幅拉动 远离异常值免费情况。

我们总想知道 离群值并尝试量化 之前尽可能的错误分布 盲目应用最大似然或最小二乘法。

现在我们已经推导出了两者之间的这种联系 最大似然和最小二乘， 我们准备扩展我们的递归最小二乘法 全公共滤波器的估计量， 20 世纪最著名的算法之一。

总而言之，我们已经了解到 最小二乘法和加权最小二乘法 产生相同的估计 给定高斯噪声的最大似然。

这一点特别重要，因为 许多复杂的噪声源，当 添加将趋向于高斯。

然而，保持警惕总是很重要的 异常值测量可以 显着影响我们的最终估计值。

在下一个模块中， 我们将看看我们现在如何 扩展我们对最小二乘法的了解 和参数估计 不断变化的状态 可能有更复杂的非线性模型 与他们有关。到时候那里见。

第 3 课补充阅读：最小二乘法和最大似然法

补充阅读：最小二乘法和最大似然法
要了解有关最小二乘法和最大似然的更多信息，请查看以下资源：

• 探索Michael Freeman 对中心极限定理的交互式解释。

• 在宾夕法尼亚州立大学的STAT 414/415网站上阅读有关最大似然的更多信息。

• 如果您是历史爱好者，您可能希望阅读这篇文章，该文章描述了最大似然法的历史及其与最小二乘法的关系。最初发表在 Statistical Science 杂志上，可在 arXiv 上免费获取。

参考

https://www.coursera.org/learn/state-estimation-localization-self-driving-cars/lecture/XcOb7/lesson-3-least-squares-and-the-method-of-maximum-likelihood