自动驾驶 9-3: 走向非线性 - 扩展卡尔曼滤波器 Going Nonlinear - The Extended Kalman Filter

Posted 2022-01-19 AI架构师易筋

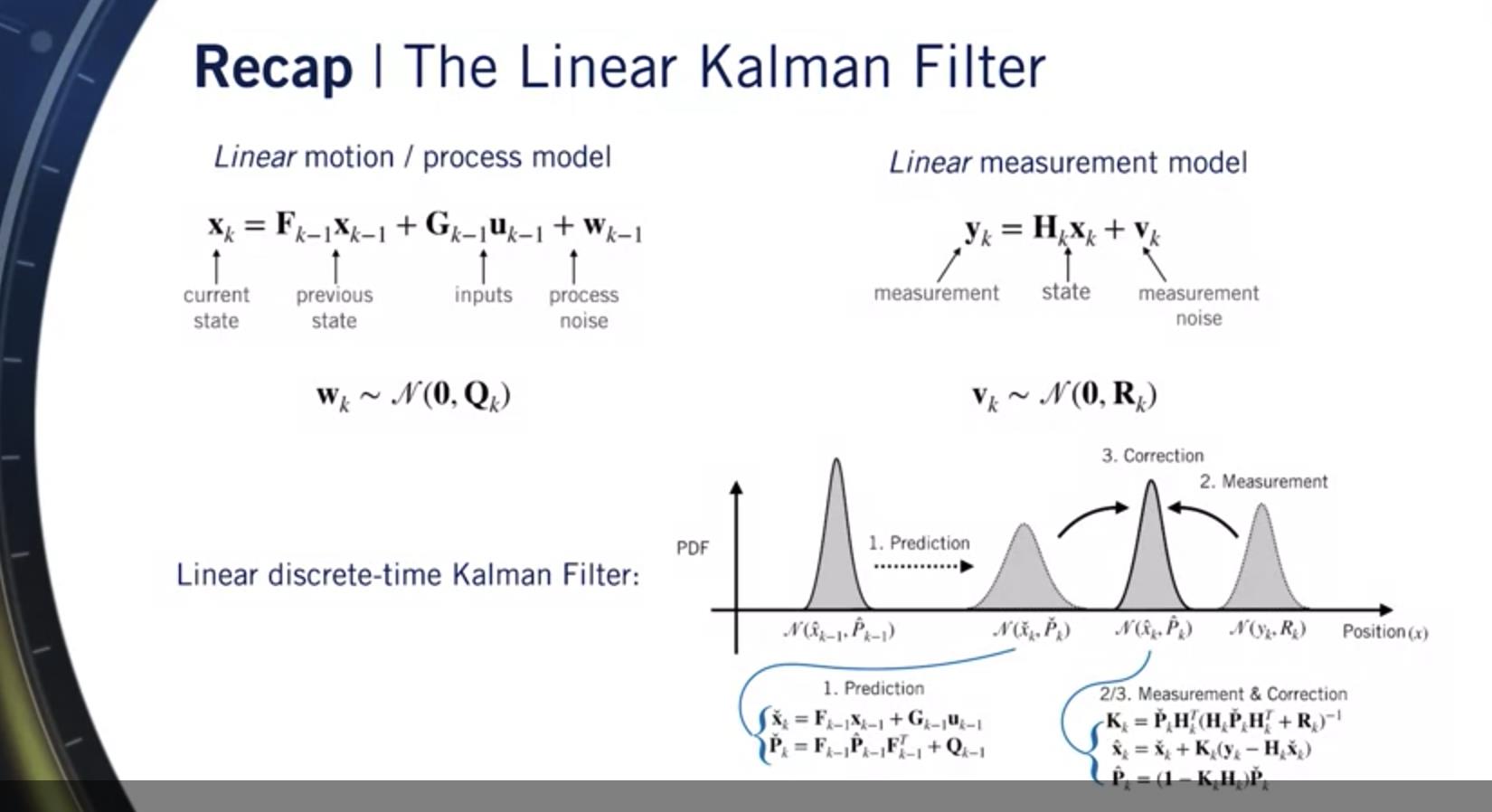
到目前为止，在这个模块中， 你已经学会了如何使用线性卡尔曼滤波器 对于状态估计， 你还看到卡尔曼滤波器是 最佳线性无偏估计器或Blue。

然而，线性卡尔曼滤波器 不能直接用于估计状态 是非线性函数 测量或控制输入。

例如，姿势 汽车包括它的方向， 这不是一个线性量。

3D 中的方向实际上存在于球体上。

所以我们需要寻找别的东西。

在本视频中，我们将了解 一种重要且广泛使用的变体 卡尔曼滤波器称为 扩展卡尔曼滤波器，或 EKF。

EKF 设计用于处理非线性系统， 它通常被认为是其中之一 状态估计的主力， 因为它被用于各种 应用包括自动驾驶汽车。

在视频结束时，您将能够； 描述 EKF 如何使用 一阶线性化转向 将非线性问题转化为线性问题， 了解雅可比矩阵在 EKF 中的作用， 以及如何计算它们， 并将 EKF 应用于简单的非线性跟踪问题。

过滤器的工作原理是首先预测均值和 更新状态估计的协方差 在某个时间步 k， 基于之前的状态和我们提供的任何输入 系统，例如油门踏板的位置。

然后过滤器使用测量模型来预测 什么测量值应该到达 基于状态估计， 并将这些预测与 实际来自我们的传感器的测量值。

卡尔曼增益告诉我们 如何称重所有这些碎片 信息，以便我们可以优化 将它们组合成一个更正的估计。

也就是说，一个新的状态和一个更新的协方差。

这有时被称为 预测器校正器架构。

正如我们在上一个视频中看到的那样， 卡尔曼滤波器实际上是最好的 线性系统的所有可能的估计量。

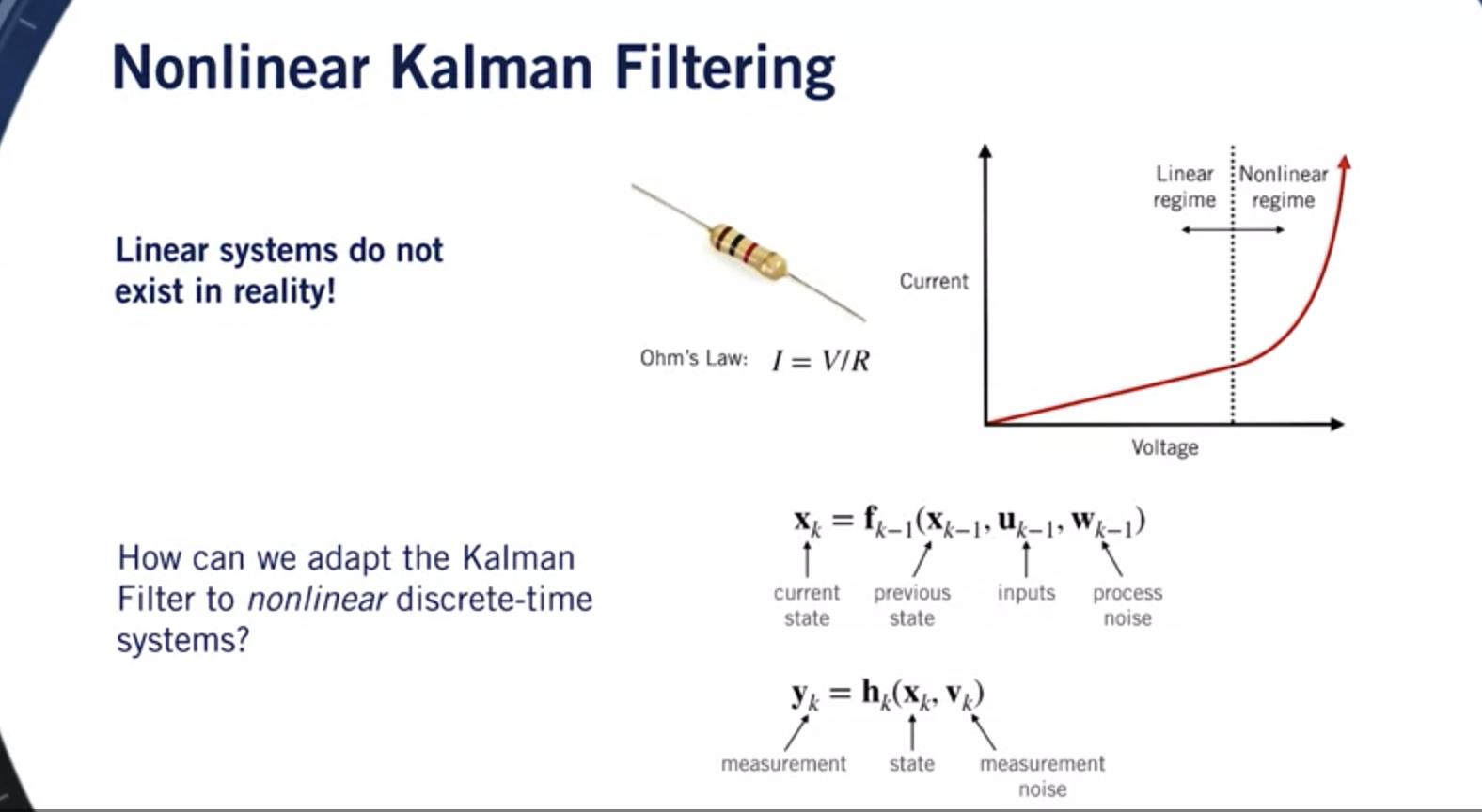
不幸的是，有一个问题。 线性系统在现实中并不存在。

即使是一个非常简单的系统，如 施加电压的电阻器不是真正线性的， 至少不是所有的时间。

对于一定范围的电压， 电流是一个线性函数 电压并遵循欧姆定律。

但随着电压升高， 电阻发热， 它以非线性方式改变电阻。

由于我们遇到的系统 实际上是非线性的， 这就提出了一个重要问题。

我们还可以使用卡尔曼滤波器吗 对于非线性系统？ 如果是这样，如何？

扩展卡尔曼滤波器的关键概念 是线性化非线性系统的想法。

出于这个原因，EKF 有时是 称为线性化卡尔曼滤波器。

线性化系统只是意味着 选择一些操作点 a， 并找到线性近似 a 邻域中的非线性函数。

在二维中，这意味着找到 x 的函数 f 的切线， 当 x 等于 a 时。

在数学上，我们通过取 函数的泰勒级数展开。

回想你的微积分课程， 你可能还记得 泰勒级数展开是一种方法 将函数表示为无限可能， 一些其条款被计算 从函数在单个点的导数。

对于线性化，我们只对 的一阶项 泰勒级数展开式以红色突出显示。

让我们回到我们一般的非线性运动 和测量模型， 并尝试将它们线性化。

我们应该选择什么作为操作点 泰勒展开式？

理想情况下，我们希望线性化 关于国家真实价值的模型， 但我们不能那样做，因为我们 已经知道状态的真正价值， 我们不需要估计它。

因此，让我们选择下一个最好的东西。

状态的最新估计。

对于我们的运动模型， 我们将对后验估计进行线性化 之前的状态， 对于测量模型， 我们将对我们的预测进行线性化 基于运动模型的当前状态。

所以现在我们在状态空间中有一个线性系统， 和矩阵 F， L、H 和 M 称为系统的雅可比矩阵。

正确计算这些矩阵是 最重要也是最困难的一步 在扩展卡尔曼滤波算法中， 也是最容易出错的地方。

但是这些雅可比矩阵到底是什么？

在向量微积分中，雅可比或雅可比矩阵是 所有一阶偏导数的矩阵 向量值函数。

雅可比矩阵的每一列都包含以下导数 函数输出相对于给定的输入。

例如，如果您的函数采用 一个三维向量和 吐出一个二维向量， 雅可比矩阵是一个二乘三矩阵。

直觉上，雅可比矩阵告诉你有多快 你的函数的每个输出都是 沿每个输入维度变化。

就像标量函数的导数如何告诉 你的输出有多快 随着输入的变化而变化。

雅可比实际上只是一个概括 多维的一阶导数。

这是雅可比矩阵的一个简单示例 具有两个输入的二维函数。

雅可比矩阵捕获 每个的一阶导数 两个输出变量 到两个输入变量中的每一个。

适应推导的最佳方式 雅可比只是练习。

尝试导出此向量值函数的雅可比行列式。

现在，我们知道如何计算 EKF 所需的雅可比矩阵， 剩下的就是将它们插入 我们的标准卡尔曼滤波器方程。

有一些差异需要注意 EKF 方程比较 我们在模块二中看到的卡尔曼滤波器方程。

首先，在预测和校正步骤中， 我们仍在使用非线性模型 传播平均值 状态估计和 计算测量残差或创新。

那是因为我们线性化了 我们关于先前状态估计的运动模型， 我们将测量模型线性化 关于预测状态。

根据定义，线性化模型正好 与非线性模型一致 在操作点。

第二个区别是外观 L 和 M 雅可比 与过程和测量噪声有关。

在许多情况下，这两个矩阵都是 身份，因为噪声通常被认为是可加的， 但情况并非总是如此。

到目前为止，这一切都非常抽象。

让我们来看看 实际使用 EKF 的具体示例。

我们将使用模块二中的相同示例， 但有一个转折。

我们将跟踪位置并 汽车沿轨道移动的速度， 但现在而不是接收 定期 GPS 测量告诉我们我们的位置， 我们将使用像相机一样的板载传感器 测量海拔高度 相对于地平线的遥远地标。

我们将保持相同的线性运动模型 就像在原始示例中一样， 并假设我们知道 地标及其位置 在全局参考系中。

因为我们的传感器正在测量一个角度， 我们的测量模型有 对汽车位置的非线性依赖。

我们需要线性化测量模型， 并在我们的扩展卡尔曼滤波器中使用它。

这个问题的雅可比矩阵看起来像这样。

注意这个问题中的 F 矩阵是 与原问题中的 F 矩阵完全相同。

那是因为我们的运动模型 在状态中已经是线性的。

还要注意噪声 Jacobian L 和 M 都是 身份，因为议案和 测量模型具有附加噪声。

尝试使用这里给出的数据来估计位置 在第一时间使用 EKF 的车辆。

这是预测步骤的结果 对于状态的均值和协方差。

注意结果是 与线性卡尔曼滤波器情况相同， 因为运动模型实际上是线性的。

对于校正步骤， 这是你应该得到的。

请记住，您应该使用 非线性测量模型 计算测量残差 不是线性模型。

另请注意，在这种情况下， 即使修正后的平均值 状态估计与预测均值不同， 校正后的协方差没有改变 来自预测的协方差。

这是因为方位角改变了 慢慢地在这个距离， 并且没有提供太多关于 车辆状态与 GPS 测量值的比较。

回顾一下，我们看到 扩展卡尔曼滤波器，或 EKF， 使用线性化采用 卡尔曼滤波器到非线性系统。

我们会遇到 我们可以应用的几种不同的非线性系统 EKF 或其表亲 UKF 在即将到来的课程项目中。

线性化通过计算工作 局部线性近似 非线性函数使用 一阶泰勒级数展开 关于一个操作点。

这需要几个雅可比矩阵， 其中包含一阶偏导数的集合。

在接下来的视频中， 我们将讨论另一种表述 EKF 称为错误状态扩展卡尔曼滤波器。 这将是一个有用的工具 在课程后期，当我们谈论 估计 3D 空间中的车辆方向。

第 3 课补充阅读：走向非线性 - 扩展卡尔曼滤波器

补充阅读：走向非线性 - 扩展卡尔曼滤波器
要了解有关非线性卡尔曼滤波和扩展卡尔曼滤波的更多信息，请查看以下资源：

• 要了解有关非线性卡尔曼滤波的更多信息，请查看Dan Simon 的这篇文章（免费提供）。

• 关于线性化及其与 EKF 的关系的详细说明可以在Dan Simon 的 Optimal State Estimation (2006) 的第 13 章第 1 节和第 2 节中找到。

参考

https://www.coursera.org/learn/state-estimation-localization-self-driving-cars/lecture/qIyk3/lesson-3-going-nonlinear-the-extended-kalman-filter#