翻译: 使用非线性卡尔曼滤波来估计信号

Posted 2022-01-19 AI架构师易筋

似乎没有特定的近似 [非线性] 过滤器始终比任何其他过滤器更好，尽管 。. . 任何非线性滤波器都比严格线性滤波器好。1

所述卡尔曼滤波器 是一种工具，估计范围广泛的过程的变量。用数学术语来说，我们会说卡尔曼滤波器估计线性系统的状态。您可能想知道系统状态的原因有两个，无论是线性的还是非线性的：

• 首先，您可能需要估计状态以控制系统。例如，电气工程师需要估计电机的绕组电流以控制其位置。航空航天工程师需要估计卫星的速度以控制其轨道。生物医学工程师需要估计血糖水平以调节胰岛素注射率。
• 其次，您可能需要估计系统状态，因为它们本身就很有趣。例如，电气工程师需要估计电力系统参数以预测故障概率。航空航天工程师需要估计卫星位置，以便智能地安排未来的卫星活动。生物医学工程师需要估计血液蛋白质水平以评估患者的健康状况。

标准卡尔曼滤波器是一种有效的估计工具，但仅限于线性系统。大多数现实世界的系统都是非线性的，在这种情况下，卡尔曼滤波器不能直接应用。在现实世界中，非线性滤波器比线性滤波器更常用，因为实际系统是非线性的。事实上，卡尔曼滤波器的第一次使用涉及 1960 年代 NASA 太空计划中的非线性卡尔曼滤波器。本文将为您提供设计和实现非线性卡尔曼滤波器所需了解的基本概念。我还将通过查看电机示例来说明非线性卡尔曼滤波器的使用。

1. 卡尔曼滤波器回顾

几年前我在这本杂志上写了另一篇关于卡尔曼滤波器的文章，但我会在这里回顾一下这个想法，供那些没有手头问题的人使用。2

如果我们想使用标准卡尔曼滤波器来估计一个信号，我们测量的过程必须可以用线性系统方程来描述。甲线性系统 是可以由以下两个方程来描述的方法：

这些方程定义了一个线性系统，因为它们不包含任何指数函数、三角函数或任何其他在图形上绘制时不会形成直线的函数。方程 1 和 2 有几个变量：

• A、B和C 是矩阵
• k 是时间索引
• x 称为系统的状态
• u 是系统的已知输入（称为控制信号）
• y 是测量的输出
• w 和v 是噪声——w 被称为过程噪声，v 被称为测量噪声

除了时间索引，这些变量中的每一个都是（通常）向量，因此包含多个元素。

在状态估计问题中，我们想要估计x， 因为它包含有关系统的所有信息。问题是，我们不能 直接测量x。相反，我们测量y，它是 被v的噪声破坏的x的函数。我们可以使用y 来帮助我们获得x的估计值，但我们不一定能从y 的表面值中获取信息，因为它被噪声破坏了。

举个例子，假设我们的系统是一辆坦克、一个移动机器人、一辆披萨送货车或其他一些直线移动的车辆。我们可以说状态由车辆位置和速度组成。输入u 是加速度，输出y 是测量位置。让我们进一步假设我们能够每T 秒测量一次位置。这个系统可以这样描述：

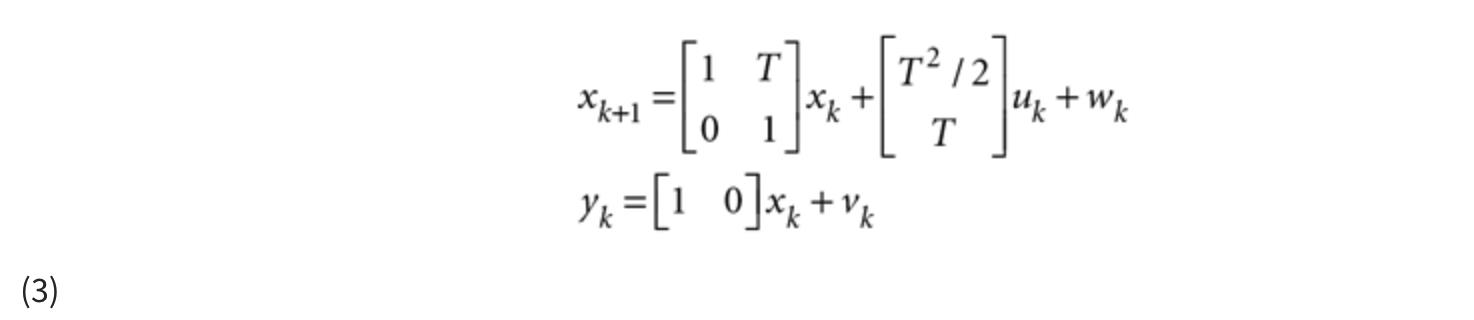
x k 是一个向量，包含车辆在时间k 的位置和速度，u k 是一个等于加速度 的标量，而y k 是一个等于测量位置的标量。3 w ^ ķ 是具有由于坑洼，在我们的知识不确定性过程噪声向量ü ķ ，和其他未建模效果。最后，v k 是一个等于测量噪声（即仪器误差）的标量。

现在假设我们想要控制车辆沿着特定路径行驶，或者我们出于其他原因想要估计车辆位置。我们可以只使用y k 作为我们的位置估计，但y k 是有噪声的。我们可以通过使用卡尔曼滤波器做得更好。这是因为卡尔曼滤波器不仅使用位置测量值y k ，还使用状态方程中包含的信息。卡尔曼滤波器方程可以写成这样：

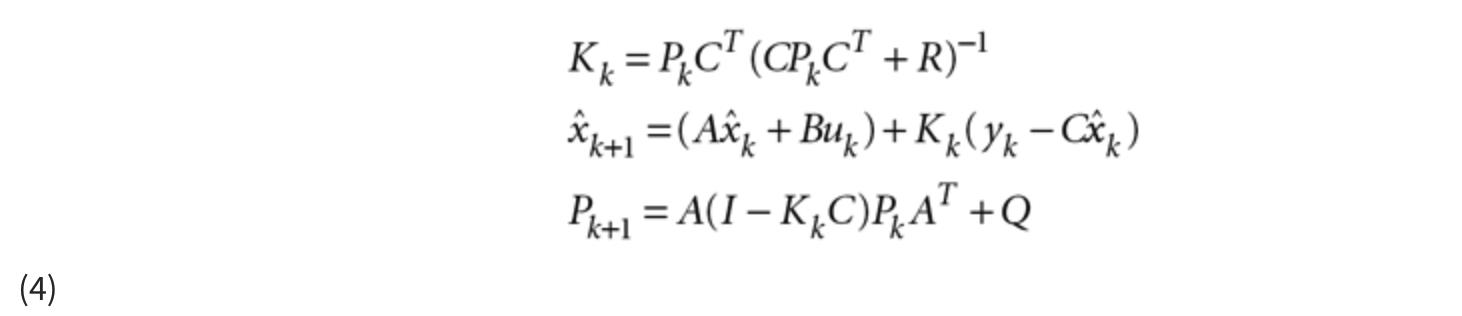
其中时间步长k = 0, 1, 2, ?? 卡尔曼滤波器再次被称为线性 滤波器，因为方程不包含任何指数函数、三角函数或任何其他不会在图形上显示为直线的函数。以下是卡尔曼滤波器方程中变量的含义：

为了初始化卡尔曼滤波器，我们需要从估计开始 初始状态为0。我们还需要从初始估计误差协方差P 0 开始 ，它代表我们在初始状态估计中的不确定性。如果我们对最初的估计非常有信心0，那么P 0 应该很小。如果我们对最初的估计非常不确定0，那么P 0 应该很大。从长远来看，这些初始化值不会对过滤器的性能产生太大影响。

2. 线性限制

好的，所以卡尔曼滤波器是一种可以应用于线性系统的线性滤波器。不幸的是，线性系统并不真正存在——所有系统最终都是非线性的。即使是简单的I = V/R 欧姆定律的关系只是有限范围内的近似值。如果电阻两端的电压超过某个值，欧姆定律就会失效。图 1 显示了通过电阻器的电流与电阻器两端的电压之间的典型关系。在小输入电压下，这种关系是一条直线，但如果电阻器消耗的功率超过某个值，这种关系就会变得非常非线性。即使是像电阻这样简单的设备也只是近似线性，即使如此也只能在有限的工作范围内工作。这说明了现实世界中不存在线性系统的事实。

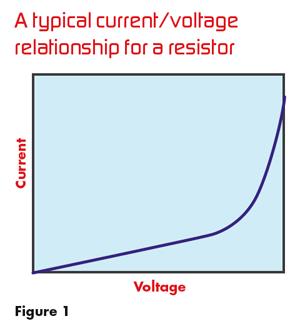
所以我们看到线性系统实际上并不存在。然而，许多系统足够接近，以至于线性估计（例如，标准卡尔曼滤波器）给出了很好的结果。但是“足够接近”只能进行到此为止。最终，我们将遇到一个即使在很小的操作范围内也不会表现线性的系统，并且标准卡尔曼滤波器不再提供良好的结果。在这些情况下，我们需要探索非线性滤波器。

非线性滤波可能困难而复杂；它当然不如线性过滤好理解。然而，一些非线性估计方法已经（或正在变得）普遍。其中包括卡尔曼滤波器的非线性扩展、“无味”滤波和粒子滤波，我的书中对此进行了解释（请参阅本文末尾的附加阅读）。

在本文中，我将讨论卡尔曼滤波器的两个最基本的非线性扩展。我刚刚总结的标准卡尔曼滤波器并不直接适用于非线性系统。然而，如果我们 将非线性系统线性化，我们可以使用线性估计方法来估计状态。为了线性化非线性系统，我们将使用一种称为泰勒级数展开式的数学工具，即将推出。

3. 泰勒级数展开

非线性卡尔曼滤波的关键是围绕标称点展开泰勒级数展开5 中系统方程的非线性项。非线性函数的泰勒级数展开可以写成：

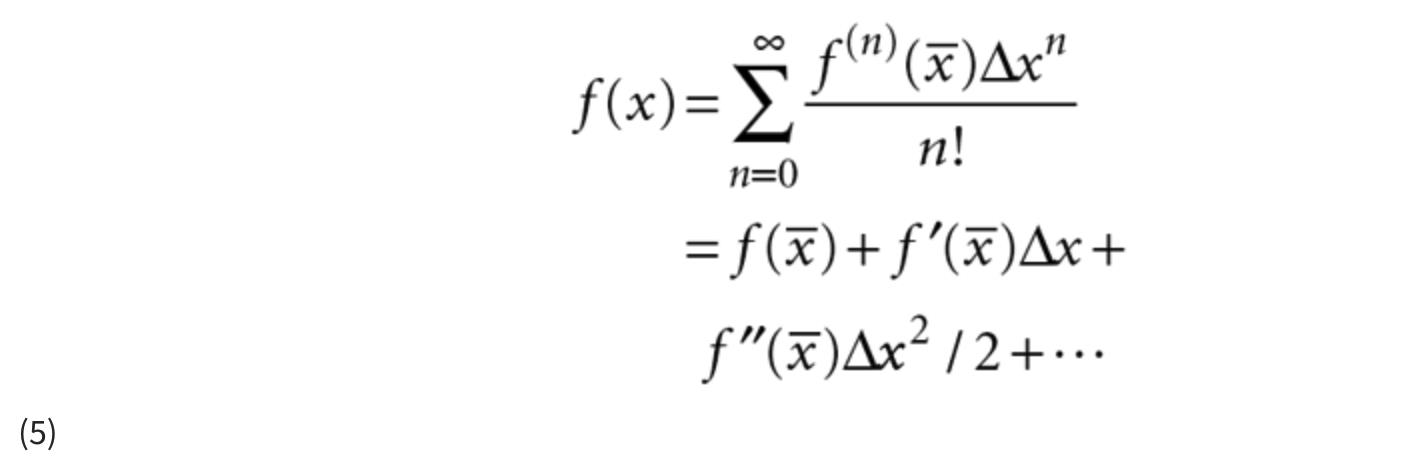
在等式 5 中：

公式 5 看起来很复杂，但实际上非常简单。让我们看一个例子。假设我们要围绕点展开泰勒级数中的f ( x ) = cos( x )= 0记住，COS（的衍生物X）为“SIN（X），并且所述衍生物罪（的X）为cos（X）。这意味着我们可以将 cos( x )的泰勒级数展开写为：

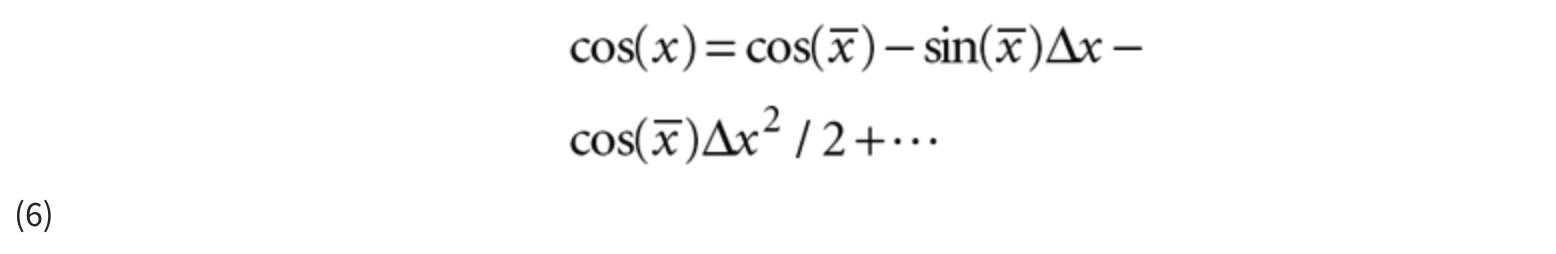
由于我们在标称点x = 0周围扩展 cos( x ) ，我们看到= 0，且 Δ x = x –= x。cos( x )的泰勒级数展开等于：

如果我们使用 cos( x )的“二阶”泰勒级数展开，我们可以说 cos( x ) 大约等于 1 – x 2 / 2。（称为“二阶”是因为它包括了到并包括x的二次幂。）换句话说，我们可以忽略泰勒级数中的其余项。这是因为泰勒级数中的附加项涉及x 的更高幂， 这些幂除以不断增加的阶乘。如果x 很小，当我们将x提高 到越来越高的幂并除以越来越大的阶乘时，泰勒级数中的附加项与低阶项相比变得无关紧要。

自己尝试一下 cos( x )的二阶泰勒级数展开式。表 1 显示了 cos( x ) 及其针对不同x值的二阶泰勒级数展开式。我们看到随着x 变小（也就是说，随着它越来越接近标称点= 0)，泰勒级数展开式可以更好地逼近 cos( x )的真实值。

线性化函数意味着围绕某个展开点以“一阶”泰勒级数展开它。换句话说，函数f ( x )的一阶泰勒级数展开等于：

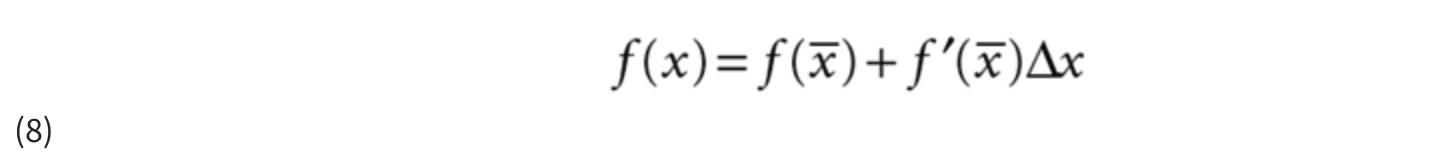
图 2 显示了函数 sin( x ) 及其围绕标称点的一阶泰勒级数展开= 0. 6请注意，对于较小的x值，图中的两条线非常接近，这表明泰勒级数展开式是 sin( x )的良好近似。但是随着x 变大，两条线会发散，因此对于较大的x值，泰勒级数展开式是一个较差的近似值。

4. 线性化卡尔曼滤波器

现在我们了解了泰勒级数，我们可以推导出线性化卡尔曼滤波器。线性化卡尔曼滤波器的基本思想是从一个非线性系统开始，然后找到一个线性系统，其状态表示 与非线性系统标称轨迹的偏差。然后我们可以使用卡尔曼滤波器来估计与标称轨迹的偏差。这种计算间接地为我们提供了非线性系统状态的估计。

这是一个一般的非线性系统模型：

方程 9 中的状态方程f ( • ) 和方程 10 中的测量方程h ( • ) 是非线性函数。例如，假设我们有一个如下所示的系统：

方程 11 中显示的状态方程有两个非线性项：平方项和余弦项。输出方程（方程 12）也是非线性的，因为它包含 1 / x k 。如果状态方程或输出方程有非线性项，则称该系统为非线性系统。

在线性化卡尔曼滤波器中，我们使用一阶泰勒级数围绕标称状态展开状态方程和输出方程。标称状态是时间的函数，因此有时称为轨迹。名义轨迹基于对系统行为可能是什么样子的猜测。例如，如果系统方程表示飞机的动力学，则标称状态可能是计划的飞行轨迹。由于建模错误、干扰和其他不可预见的影响，实际飞行轨迹将与此标称轨迹不同。但我们希望实际轨迹会接近 到标称轨迹，在这种情况下，泰勒级数线性化应该相当准确。非线性系统方程和输出方程的泰勒级数线性化给出：

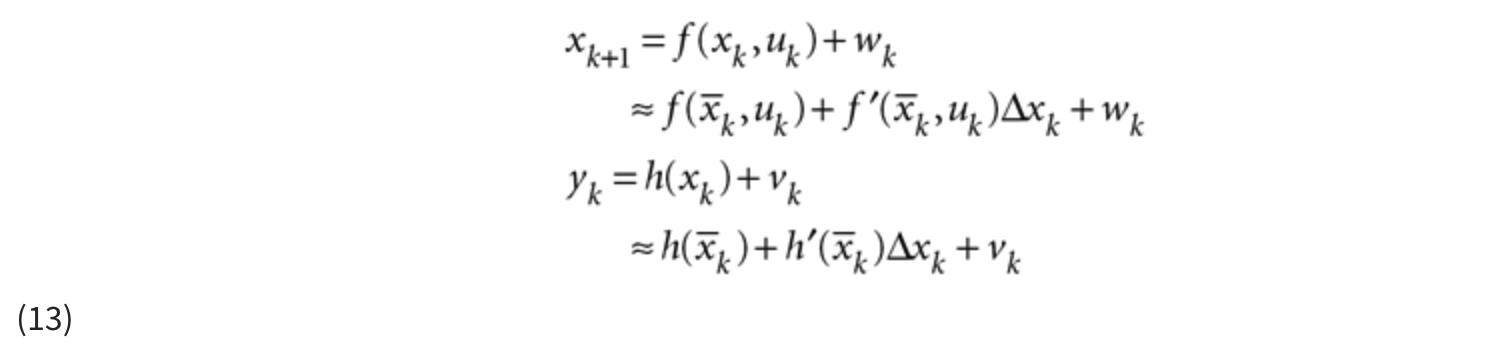
现在请注意，与标称轨迹的偏差可以写为：

结合等式 13 和 14 给出：

现在看看我们已经完成了什么——我们有状态方程和输出方程，它们是x 的线性函数。这意味着我们可以使用标准卡尔曼滤波器来估计 Δx。

使用线性化卡尔曼滤波器时要记住两个要点：

下面是线性化卡尔曼滤波器算法的总结：

1. 系统方程如下：
   
2. 名义轨迹提前已知：
   
3. 在每个时间步，计算以下偏导矩阵，在标称状态下评估：
   
   上式中的导数是关于x k 的 。本文稍后将给出偏导数矩阵的一个例子。

5. 执行以下卡尔曼滤波器方程：

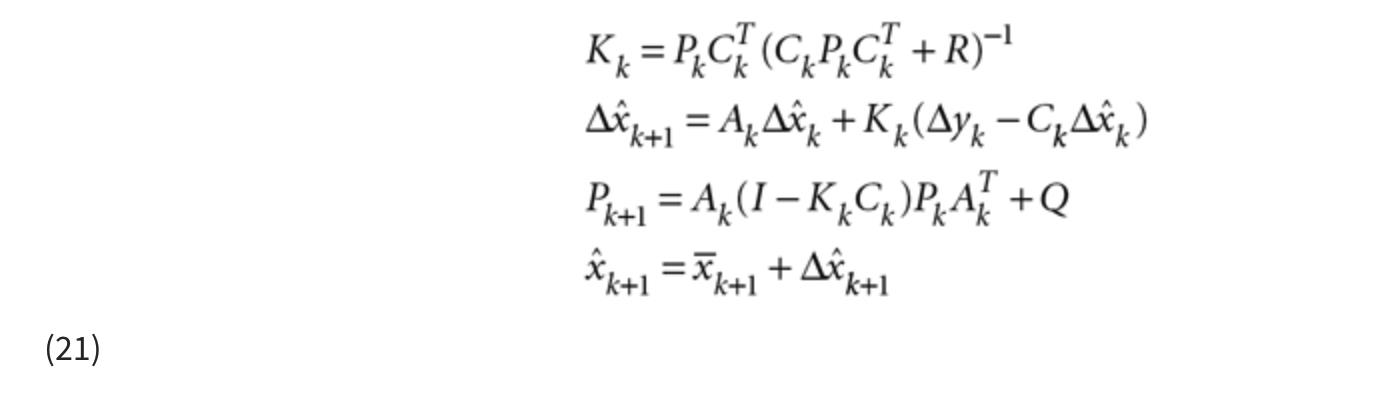
5. 扩展卡尔曼滤波器

我们推导出的线性卡尔曼滤波器就它而言是好的，但有一个问题：我们需要知道标称轨迹提前时间。对于某些系统，我们可能提前知道标称轨迹（例如，具有预定飞行计划的飞机飞行或在制造环境中移动的机械臂），但对于其他系统，我们可能无法知道标称轨迹。

EKF（扩展卡尔曼滤波器）的想法是使用我们对x的估计 作为线性化卡尔曼滤波器中的标称轨迹。换句话说，我们设置 等于 在线性化卡尔曼滤波器中。这是一种巧妙的状态估计引导方法；我们使用的标称轨迹估计X 和使用的估计值X 为额定轨迹。在将这些代入线性化卡尔曼滤波器方程并经过一些数学运算后，我们得到以下 EKF 算法：

1. 系统方程如下：
   
2. 在每个时间步，计算以下导数矩阵，在当前状态估计值处评估：
   
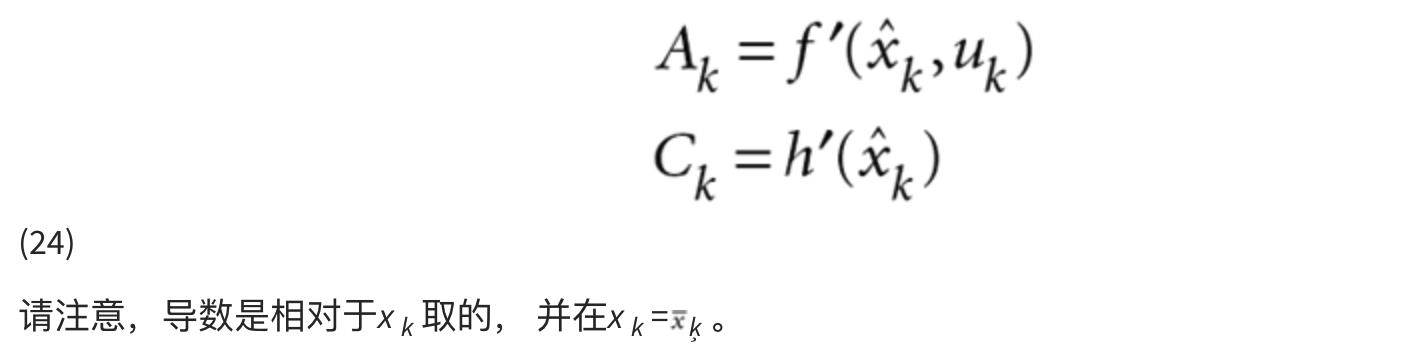
3. 执行以下卡尔曼滤波器方程：
   

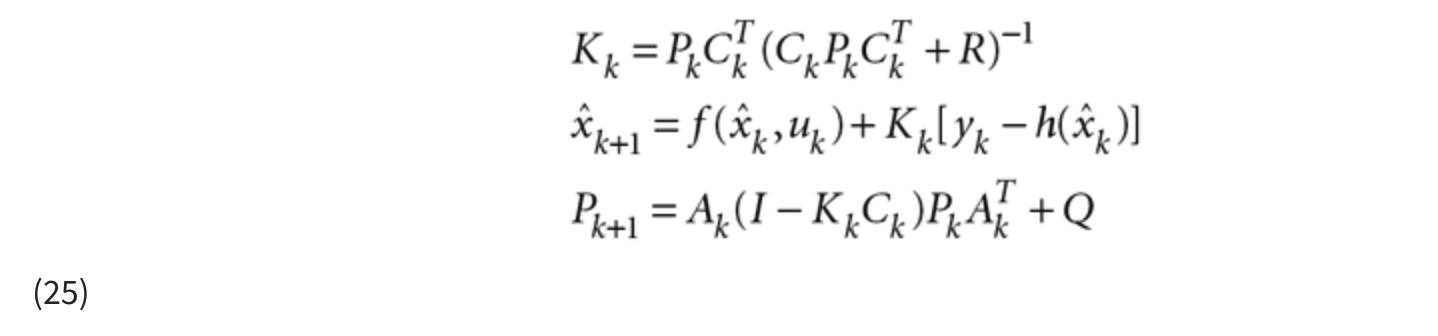
6. 电机状态估计

为了说明 EKF 的使用，让我们用它来估计两相永磁同步电机的状态。我们可能想要估计状态，以便我们可以使用控制算法来调节它们，或者我们可能想要估计状态，因为我们出于其他原因想知道电机的位置或速度。假设我们可以测量电机绕组电流，并且我们想使用 EKF 来估计转子位置和速度。系统方程为：

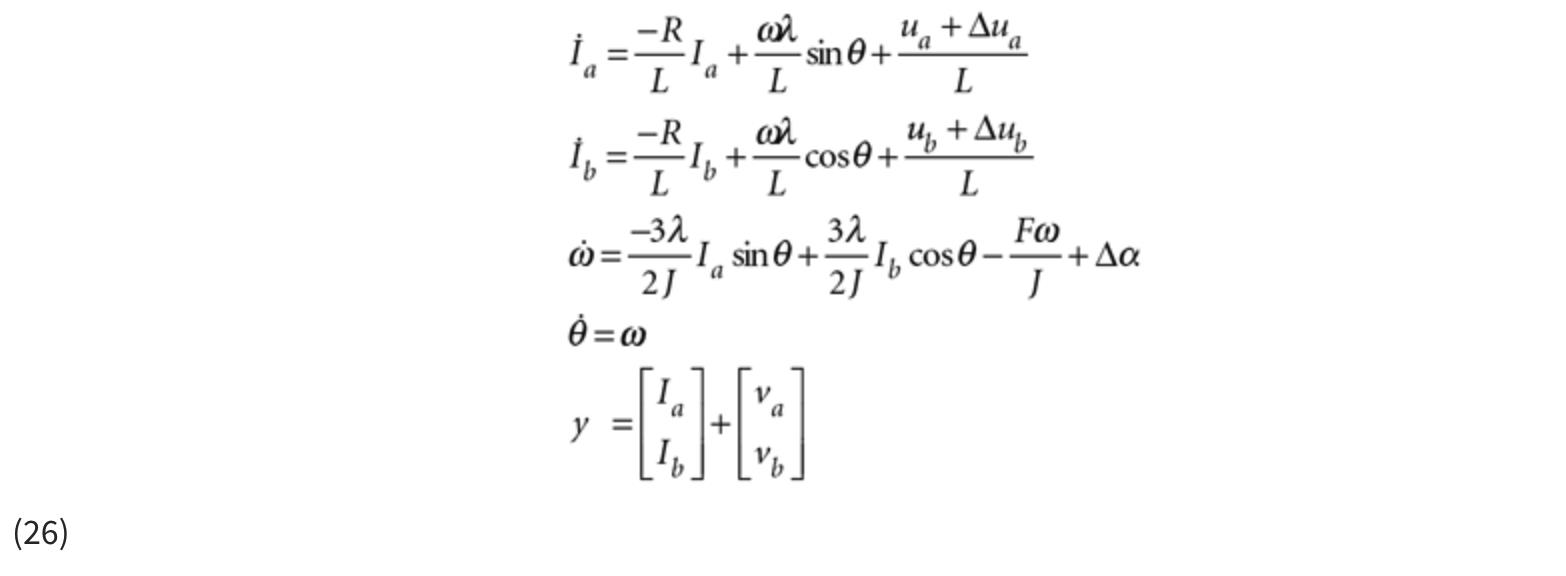
这些方程中的变量定义如下：

如果我们想对电机应用 EKF，我们需要定义系统的状态。您可以通过查看系统方程并注意导数出现的位置来查看状态。如果一个变量在系统方程中是微分的，那么这个量就是一个状态。所以我们从方程 26 所示的运动方程中可以看出，我们的系统有四种状态，状态向量x 可以定义为：

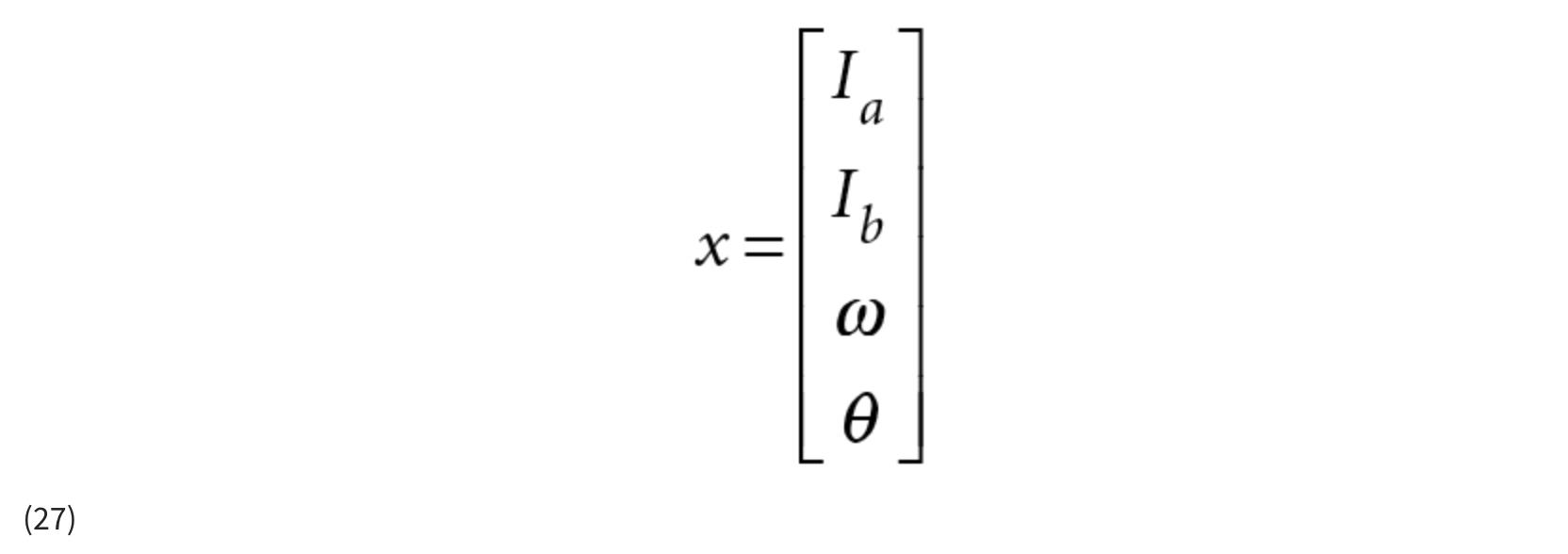
系统方程是通过“离散”微分方程获得方程 28 中的方程，其中 Δ t 是我们在微控制器或 DSP 中用于估计的步长。

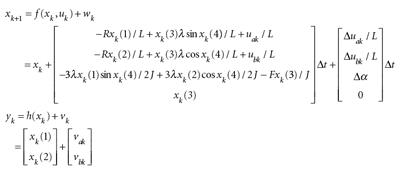
要使用 EKF，我们需要找到f ( x k , u k ) 和h ( x k ) 关于x k 的导数 。这是一个新的转折，因为f ( x k , u k ) 和h ( x k ) 都是向量x k 的 向量函数。我们如何找到一个向量相对于另一个向量的导数？如果您已经知道如何取导数，那么找到向量的导数其实并不难。例如，如果我们写向量f 和x 为：

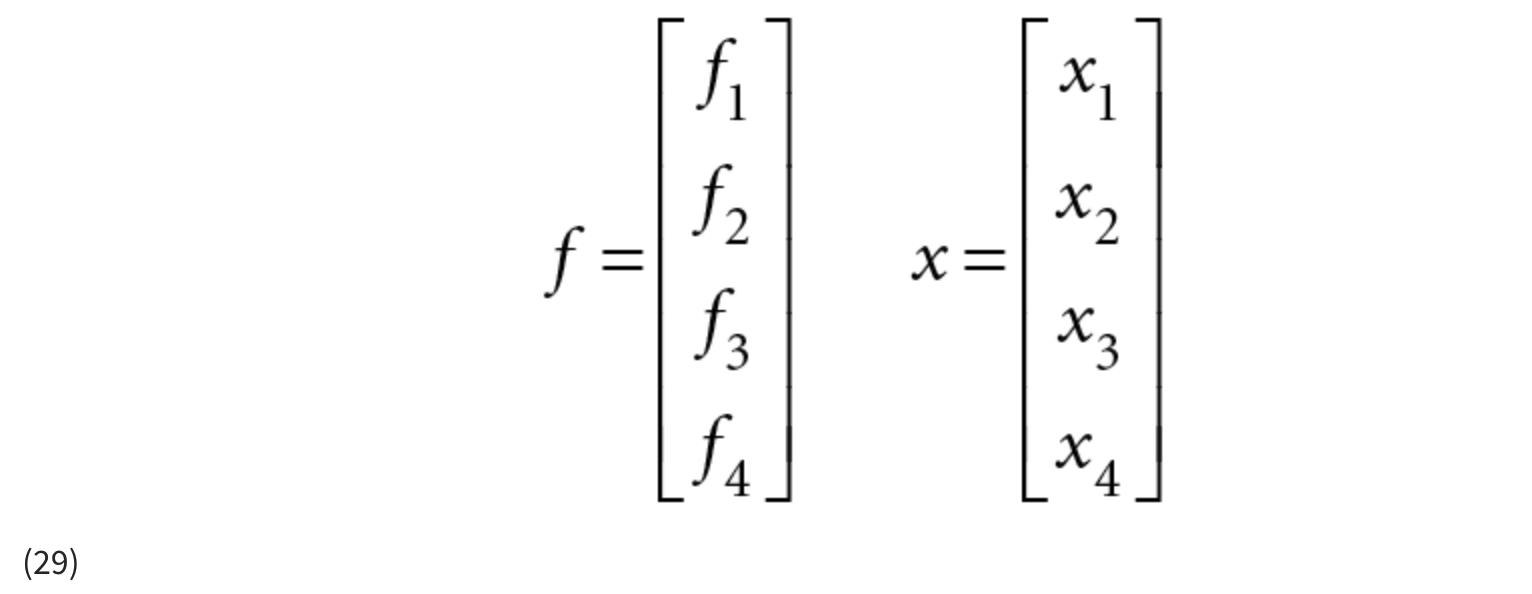
那么f 对x的导数 等于 4 × 4 矩阵，如公式 30 所示：

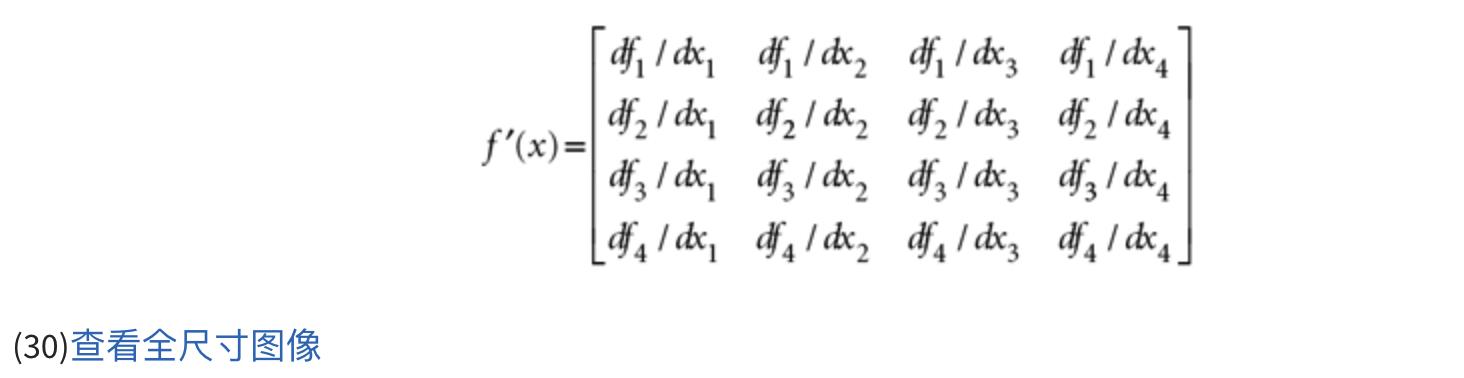
这个矩阵可以推广到任何大小的向量f 和x。有了这个背景，我们现在可以找到如公式 31 所示的导数矩阵：

让我们模拟 EKF，看看我们可以如何估计转子位置和速度。我们将假设测量噪声项v ak 和v bk 是标准偏差等于 0.1 安培的零均值随机变量。控制输入​​（绕组电压）等于：

方程 32 意味着在离散时间内，控制输入等于：

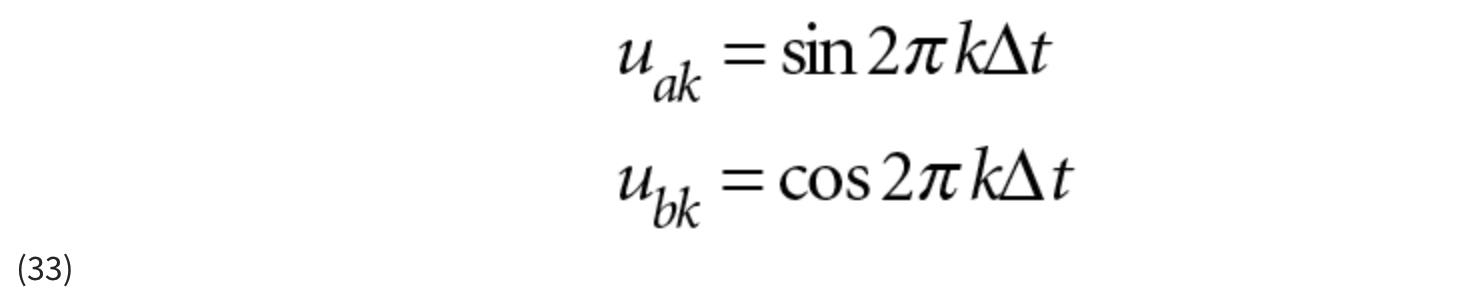
施加到绕组电流的电压等于这些值加上u ak 和u bk ，我们假设它们是标准偏差等于 0.001 安培的零均值随机变量。我们还将假设由于负载扭矩干扰 α k 引起的噪声 具有 0.05rad/sec 2的标准偏差。即使我们的测量值仅包含绕组电流，我们也可以使用 EKF 来估计转子位置和速度。我使用 Matlab 来模拟电机系统和 EKF。清单 1 显示了代码，图 3 显示了仿真结果。我们看到转子位置和速度估计得很好。

参考

https://www.embedded.com/using-nonlinear-kalman-filtering-to-estimate-signals/