数据结构与算法之深入解析“石子游戏IV”的求解思路与算法示例

Posted 2022-01-17 Forever_wj

一、题目要求

• Alice 和 Bob 两个人轮流玩一个游戏，Alice 先手。
• 一开始，有 n 个石子堆在一起，每个人轮流操作，正在操作的玩家可以从石子堆里拿走任意非零平方数个石子。
• 如果石子堆里没有石子了，则无法操作的玩家输掉游戏。
• 给你正整数 n ，且已知两个人都采取最优策略，如果 Alice 会赢得比赛，那么返回 True ，否则返回 False。
• 示例 1：

输入：n = 1
输出：true
解释：Alice 拿走 1 个石子并赢得胜利，因为 Bob 无法进行任何操作。

• 示例 2：

输入：n = 2
输出：false
解释：Alice 只能拿走 1 个石子，然后 Bob 拿走最后一个石子并赢得胜利（2 -> 1 -> 0）。

• 示例 3：

输入：n = 4
输出：true
解释：n 已经是一个平方数，Alice 可以一次全拿掉 4 个石子并赢得胜利（4 -> 0）。

• 示例 4：

输入：n = 7
输出：false
解释：当 Bob 采取最优策略时，Alice 无法赢得比赛。
如果 Alice 一开始拿走 4 个石子， Bob 会拿走 1 个石子，然后 Alice 只能拿走 1 个石子，Bob 拿走最后一个石子并赢得胜利（7 -> 3 -> 2 -> 1 -> 0）。
如果 Alice 一开始拿走 1 个石子， Bob 会拿走 4 个石子，然后 Alice 只能拿走 1 个石子，Bob 拿走最后一个石子并赢得胜利（7 -> 6 -> 2 -> 1 -> 0）。

• 示例 5：

输入：n = 17
输出：false
解释：如果 Bob 采取最优策略，Alice 无法赢得胜利。

二、求解算法

① 动态规划

• 我们用 f[i] 表示先手在面对 i 颗石子时是否处于必胜态（会赢得比赛），由于先手和后手都采取最优策略，那么 f[i] 为必胜态，当且仅当存在某个 f[i−k²] 为必败态。也就是说，当先手在面对 i 颗石子时，可以选择取走 k² 颗，剩余的 i−k² 颗对于后手来说是必败态，因此先手会获胜。
• 可以写出状态转移方程：

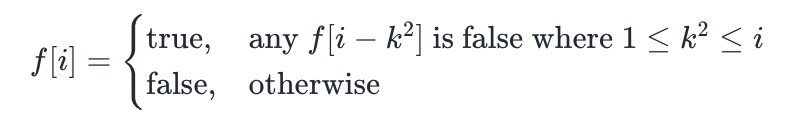
• 边界条件为 f[0]=false，即没有石子时，先手会输掉游戏。
• 最终的答案即为 f[n]。
• C++ 示例：

class Solution 
public:
    bool winnerSquareGame(int n) 
        vector<int> f(n + 1);
        for (int i = 1; i <= n; ++i) 
            for (int k = 1; k * k <= i; ++k) 
                if (!f[i - k * k]) 
                    f[i] = true;
                    break;
                
            
        
        return f[n];
    
;

• Java 示例：

class Solution 
    public boolean winnerSquareGame(int n) 
        boolean[] f = new boolean[n + 1];
        for (int i = 1; i <= n; ++i) 
            for (int k = 1; k * k <= i; ++k) 
                if (!f[i - k * k]) 
                    f[i] = true;
                    break;
                
            
        
        return f[n];
    

② 双人博弈通用解法—记忆化 DFS

• AB 双方博弈问题的两个关键点:
• • 用元组记录结果，本题不需要，A 为 true，B 即为 false；
• • A 先手完， 以剩下的石子看 B 是先手；
• dfs 搜索每次能拿的各种情况，有一种赢则能赢。
• Java 示例：

class Solution 

    Boolean dp[];
    public boolean winnerSquareGame(int n) 
        dp = new Boolean[n + 1];
        return dfs(n);
    

    private boolean dfs(int n) 
        if (n == 0) 
            return false;
        
        if (dp[n] != null) 
            return dp[n];
        
        // 拿i个， 遍历所有情况， 有一种赢即赢
        for (int i = 1; i * i <= n; i++) 
            // res为对方的博弈结果， res为false即自己赢
            boolean res = dfs(n - i * i);
            if (!res) 
                dp[n] = true;
                return true;
            
        
        dp[n] = false;
        return false;