Facebook路由事故未圆，何以元宇宙？

Posted 2022-01-17 beyondma

最近Facebook创始人马克·扎克伯格正式对外宣布，Facebook将更名为Meta。“Meta”一词来自于最近Facebook火爆全球的概念元宇宙（Metaverse），据说Facebook此举是用改名来彰显公司在元宇宙世界中开拓和创新的愿景。

 

据我所知这不是Facebook第一次改名，熟悉Facebook成长纪传题材电影《社交网络》的同学，可能对于其中人物肖恩的经典台词“Drop the ‘The’. Just Facebook. It's cleaner.“印象非常深刻，不得不说当时这一改是神来之笔，Facebook的确是比” The Facebook“更加简洁、响亮，但是这次Facebook丢掉的可不是定惯词The,而是宇宙Verse。按照我的理解这大概可以认为Facebook可以做Meta元的概念，但是不是能做成宇宙就无从知晓了。

这也不是Facebook第一次宣布All In一个概念，2019年他们发布了基于区块链的数字货币-Libra，不过Libra的发展之路却是各种坎坷，有意思的是去年年底Libra也改名为Diem了，而且据说这次Facebook改为Meta之后也会重点与区块链的最新概念NTF相结合，Facebook这种打不过就改名的方式是否值得我们学习，也值得观察。

当然笔者并不关心以上这些和技术无关的科技新闻，这里笔者想探讨的话题是不久之前FaceBook发生的那次由于BGP路由协议配置错误造成的史诗级中断事故，在当时故障期间FaceBook所有旗下APP全面对外服务中断，而且故障的时间长达7个小时之久。针对这个话题我也写过一篇博客《一行小错为何产生巨大破坏-Facebook史诗级故障大反思》进行过总结，而如果这次Facebook真的要All In元宇宙，那么有关网络路由协议的问题还需要进一步的优化，不彻底解决网络方面的问题，只是创造一个时常宕机的元宇宙的话，没有任何意义。

路由协议的核心问题到底是什么？

所谓路由协议，归根结底就是要找到从起始点S出发到目的地点D的最短路径。这其实也就是我们熟知的旅行规划问题，要通过算法回答旅行者从S城市出发如何以最小的代价达到城市D。而针对这个问题早就有经典算法dikjstra解决。

由于网上能搜索到的现成算法大多是根据Leecode等算法网站上的原题给出的答案，运算结果只输出起点和终点的距离和费用，既没有记录具体的行走路径，也没有详细介绍算法的思想，为了说清这个问题下面我们先把dikjstra算法做一下介绍。

​再读旅行规划题目

旅行规划的题目可以归结为以下说法，一张自驾旅游路线图显示了城市及公路的数量，高速公路长度、过路费。现在要通过一个算法，找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的，那么需要输出最便宜的一条路径。

实际在网络路由规划中，城市代表着网络上的节点，调整公路代表网络上的通道，公路长度一般代表网络通道的传输性能，过路费用的数据在实际工程中可能代表着线路质量等参数。

示例代码中的变量说明：N、M、S、D分别代表城市个数、调整公路条数、旅行者起始城市编号、旅行者目的地城市编号，其中N（2≤N≤500）是城市的个数，三维数组g存储高速公路的信息，记录起始城市、终点城市、高速公路长度、收费额，如g[i][j][1]代表编号为i的城市到编号为j的城市之间的距离，g[i][j][2]代表编号为i的城市到编号为j的城市过路的费用，​哈希表Path记录由旅行者的起始城市S到编号为i的城市之间的最短路径信息，如起始城市S到i之间经过j、k最短，那么Path[i]的值应该是[j,k]，注意j、k对于顺序敏感。Dist数据记录旅行者起始市S到编号为i的城市之间的距离数值，cost数据记录旅行者起始市S到编号为i的城市之间的花费，到Known数组记录城市是否被算法遍历确认，

比如经典路由协议OSPF (Open Shortest Path First)中的SPF最短路径优先其实就非常清楚的表达出了dijkstra算法的精髓，实际上这个算法就是不断找到离起点S最近的未确认城市A，并尝试通过A中转能否优化到S的距离，如下图所示：

 

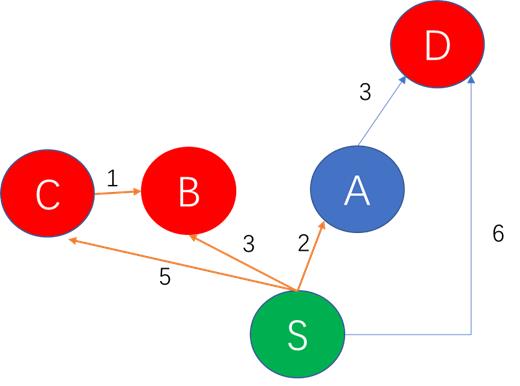
注：绿色代表起点城市

蓝色代表known状态已经迭代的城市

红色代表unknown状态的城市

dijkstra算法首先要做的就是找到所有未知节点中与起始地S最近的城市A，因为经城市A现在离S最近，那么经城市A中转，就有可能会缩短S到其它目的地城市D的距离。比如上图当中S到A的距离是2，截止目前是S到其它城市中距离最短的一条路径，那么经A跳转则有可能获得一个比从S直接到D更短的路径。在上图例中在使用A行过一轮迭代以后，S到D的距离可以由直接访问的距离6，优化为经A中转的距离5。在完成一轮优化后A节点会被记录为known的状态，接下来会用非known状态的节点中找到离起始点最近的那个做下一轮迭代。如下图所示：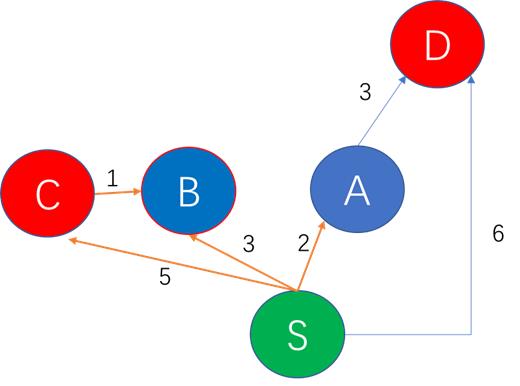

 

如图所示，这轮迭代中距离起始点D最近的城市是B那么，算法会重复刚刚的步骤，尝试通过B中转去起点S优化到其它unknown状态城市的距离，在这个例子中，可以将由S到C的距离优化到4，迭代完成后b会被标识为known状态，算法持续迭代，直到所有城市全部状态全部都是known为止。

以go语言为例，代码如下：

package main



import (

       "fmt"

       "strconv"

)



const N int = 4

const INF int = 501



var g [N][N][2]int

var dis [N + 1]int

var pay [N]int



var known [N]bool

var n, m, s, d, i, j, t1, t2, v int

var path map[int][]int



func findMinDistance() 

       
       disMin := INF
       for i := 0; i < n; i++ 
             if !known[i] && dis[i] < disMin 
                    v = i
                    disMin = dis[i]
             
       


func dijkstra() 

       for k := 1; k < n; k++ 

             findMinDistance()//先把状态为unknown的节点中到起点距离最短的点

//接下来按照之前介绍的算法使用距离最短的节点对其它节点进行优化

             known[v] = true

             for i = 0; i < n; i++ 

                    if !known[i] && g[v][i][0] < INF 

                          if dis[v]+g[v][i][0] < dis[i] 

                                 dis[i] = dis[v] + g[v][i][0]

                                 pay[i] = pay[v] + g[v][i][1]



                                 footPrint := path[v]

                                 path[i] = append(footPrint, v)

                           else if !known[i] && dis[v]+g[v][i][0] == dis[i] && pay[v]+g[v][i][1] < pay[i] 

                                 pay[i] = pay[v] + g[v][i][1]

                          

                    

             



       





func main() 

//以下是初始化城市个数、高速公路条数、起始城市、终点城市的工作

       path = make(map[int][]int)

       n = 4

       m = 5

       s = 0

       d = 3

       //初始化时先把path对应的路径置为空

       for i := 0; i < n; i++ 

             s1 := make([]int, 0)

             path[i] = s1

       

       //初始化化时先把g数组对应的路径置为空

       for i = 0; i < n; i++ 

             for j := 0; j < n; j++ 

                    g[i][j][0] = INF

                    g[i][j][1] = INF

             

       

       keyInput := [...][5]int0, 1, 1, 20, 1, 2, 3, 30, 0, 3, 40, 10, 0, 2, 10, 20, 2, 3, 2, 20

//把道路信息写入g数组

       for ; m > 0; m-- 

             i = keyInput[m-1][0]

             j = keyInput[m-1][1]

             t1 = keyInput[m-1][2]

             t2 = keyInput[m-1][3]



             g[i][j][0] = t1

             g[j][i][0] = t1

             g[i][j][1] = t2

             g[j][i][1] = t2

       

       //fmt.Println(g)

//初始化known数组全部置为false状态

       for i = 0; i < N; i++ 



             known[i] = false



       

       //初始化起点到编号为j节点的距离及花费信息

       for j = 0; j < n; j++ 

             dis[j] = g[s][j][0]

             pay[j] = g[s][j][1]

       

       dis[s] = 0

       pay[s] = 0

       dis[n] = INF



       dijkstra()//调用dijkstra算法



       if dis[d] < INF 

             fmt.Println("Distance is " + strconv.Itoa(dis[d]) + ",The cost is " + strconv.Itoa(pay[d]))

             fmt.Println("Path is", path[d])

       

在例程中各城市之间的关系如下，

 

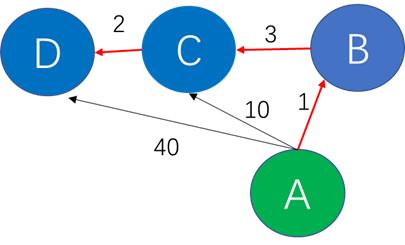
从A(0号城市)到D（3号城市）的最短路径需要经B（1号城市）和C(2号城市)中转，路径用红色标出

代码运行结果如下：

Distance is 6,The cost is 70

Path is [1 2]

符合预期。

路由协议的核心问题到底是什么？

在聊完经典算法dikjstra之后我们终于可以结合网络当中的实际应用，也就是路由协议的话题了，其实现在各种路由协议的坑本质上都是从dijkstra算法继承而来的，当然这里并不是说dijkstra算法不优秀，而是他与路由算法的角度不同，笔者总结路由协议存在的问题，主要是由以下几方面造成的。

   Dijkstra本质上是旅行者算法而不是网络路由算法

简单来讲dijkstra是为旅行者而设计的，站在旅行者的角度去考虑问题，但是从网络的实际使用情况上看，算法中的旅行者对应应用层的数据包，按照网络结构层的分工界限，应用层只负责提供目的IP地址，具体如何路由到目的IP，完全不是数据包的发送方需要关心的问题。

而站在网络设备的角度上看，假如上面例程中的城市A是上台路由器，那么它上只需要掌握最优路径上下一个城市C的路由信息就可以了，掌握整个路径的全貌，费时费力不说，也没有必要。

 

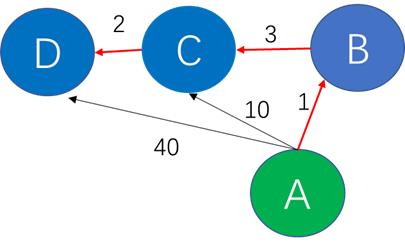
但在实际工程中如果不存整个最优路径的整体路由信息，就可能会成环，

 

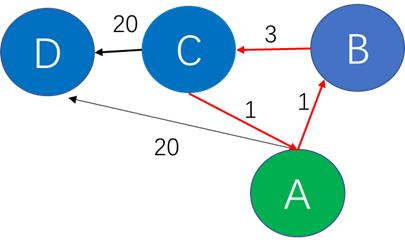
以上图为例，A节点认为发送给D的包应该经过B，B认为包应该经过C，C的路由表又把包路由给A，也就是数据包会在这个网络环里转圈，永远也出不去，像BGP协议去环的主要方法就是查看路由信息里是否包含了自身的AS编号，如果包含则拒绝接收。但鱼与熊掌不可兼得，要想完全避免环路，就要牺牲一定的效率，在目前djklstra算法框架下建立的路由协议，都要面临这个选择，这可能也是未来路由协议优化的一个重要方向。

Dijkstra算法的时间复杂度决定路由协议要么限制节点数，要么将将网络分区。

熟悉算法的小伙伴肯定一眼就能看出来，Dijkstra算法的时间复杂度接近于O(n*n)。而且我们刚刚也讲了Dijkstra每步迭代的之间是有前后顺序关系的，很难像搜索那样进行分布式并行计算改造。因此这也就使得路由协议必须要限制管理节点的个数，因为如果要给整个互联网上几十亿节点跑一遍Dijkstra算法，显然不是一种可行的计算方案。

而降低管理节点的方式有两种，一种是把网络分区，外部网关协议EGP只处理区和区之间的路由，内部网关协议IGP只处理区域内部的网络关系。这也是为什么路由协议会分为EGP外部网关协议和IGP内部网关协议两大类协议的根本原因。

外部网关协议中的BGP把整个互联网分为几万个自治区（AS），内部网关协议OSPF协议要把网络分为不同AREA本质上都是受Dijkstra算法时间复杂度的影响而做出的妥协。当然也可以直接限制管理的网络节点个数，比如RIP就把路由的步数设置在了16跳以内，这在处理小规模网络区域时也不失一个好的方式。

当然本文只是把问题提出来了，具体怎么优化解决，笔者也正在思考，目前也没有答案，如果各位读者有好的想法欢迎私信或者留言。最后笔者还是要重申一下，如果Facebook对于刚出的史诗级故障都没给出一个靠谱的解决升级建议，就忙着去炒作什么元宇宙，那这样造出来的元宇宙可能稳定性也会堪忧。