常见的变换总结与代码：DCT，STFT，K-L变换等

Posted 2022-01-17 yufan_fw

文章目录

• 前言
• 一、从DFT到DCT
• 二、从CTFT到STFT
• 三、K-L变换与降维思想
• 四、K-L变换实例：人脸识别（含代码和详细注释）
• 五、参考资料

前言

  之前学信号和DSP的时候，除了常见的离散傅里叶变换之外，还看过诸如离散余弦变换（DCT），短时傅里叶变换（STFT），小波变换等等，这些变换看似繁多且杂乱无章，但其实其背后的思想都是变换域的思想，引入某种变换，通常是正交变换，将时间相关的信号序列变换到另一个域上来进行分析。其实我觉得理解了这个思想之后，不需要太关注公式的推导，大致了解思想简单推导一下即可，毕竟有很多的包和函数都是集成化的。特此在这里做一个思路和代码的总结，由于小波变换相对没有那么常用，此处总结DCT，STFT和K-L变换。

一、从DFT到DCT

  DCT全名为离散余弦变换，当然与之相对应的有离散正弦变换。事实上，DCT变换族中有16个成员，包括8种DST和8种DCT，具体对其进行划分的方式则是根据原始序列做对称的方式的不同来进行划分。例如：对称点两侧的序列是对称还是反对称，是轴对称还是中心对称，对称点是在离散序列的采样点上还是不在……总之，不同的对称形式决定了不同的DCT形式，这个公式具体的推导可以去参考一下比较经典的数字信号处理的教材，其公式推导的核心思想也就是运用了DFT中旋转因子的对称性。但是在本篇博客中主要关注的还是对思想的理解，以及结果代码的实现。
  我们先来回顾一下经典的DFT公式的表达形式，其中：$W_N^{kn}=e^{-j\frac{2\pi }{N}kn}$

  其对应的展开形式如下：

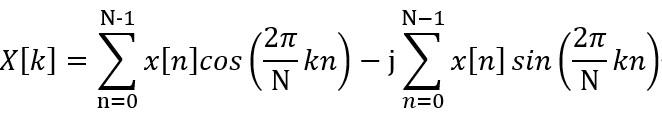
  而在各种DCT和DST中，最常见的是2型DCT，因为其具有较好的能量压缩性质。因此接下来主要讨论2型的DCT，其公式如下：

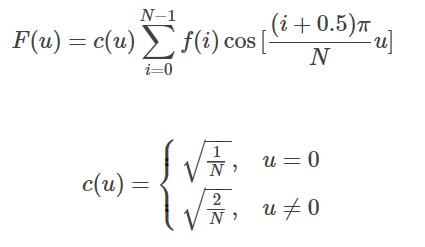
  这也属于一种正交变换，其本质原因是因为DCT的正交基还是没有脱离三角函数系，其采用的是余弦正交基，而余弦，正弦和复指数基本身就具有正交性。
  我们可以比较一下DCT和DFT的展开形式，很容易发现：DCT中全为实数，没有复数，且只有余弦项，这降低了数值计算的复杂度，仔细分析就会发现，其实DCT中之所以只有实数，恰恰是因为利用了离散序列的对称性，类似于$e^{jwn}+e^{-jwn}$的形式得到的就是实数序列。

// 一维DCT函数代码如下，输入一个向量，得到一个向量，因此就不专门写主函数了

function output = dct(input)
%The One-dimensional DCT,input is a vector
    N = length(input);
    for i = 0:N-1
        if i==0
            a = sqrt(1/N);
        else
            a = sqrt(2/N);
        end
        sum = 0;
        for j = 0:N-1
            sum = sum+input(j+1)*cos(pi*(j+0.5)*i/N);
        end
        output(i+1) = a * sum;
    end
end

  仿真结果部分，这里参考了一位同学汇报的PPT，下图是原信号的时域离散波形：

  而下图则为该信号进行了DFT和DCT之后的结果：

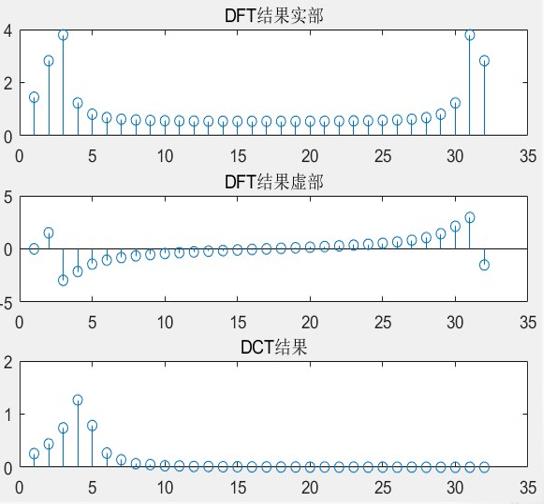
  我们可以看到，有限长序列的2型DCT的系数通常比使用DFT得到对应的系数，更多集中在较低序号（对应较低频率）的部分（这个个人觉得可以从另一个角度去理解，做FFT时，高频部分一定会存在有低频部分的镜像分量，如上图“DFT实部和虚部“”的结果所示，但DCT可以避免这个问题），且我们发现在一般情况下，往往剩余部分的系数趋近于0，如上图的“DCT结果”部分所示，因此，说明DCT往往比DFT具有更好的能量压缩性质，因此，二维的DCT往往用于图像的压缩，例如我们熟悉的 图像JPEG标准。
  接下来，我们从一维DCT过度到二维DCT，二维DCT的公式如下：

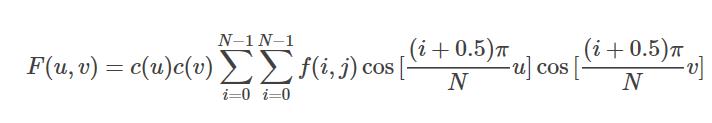
  类比一维DCT，将上式写成矩阵形式，其中$c(i)$的取值同一维情况：

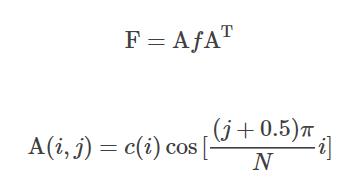
  同样给出二维DCT的函数：

function output= dct2(input)
% Two-Dimensional DCT,input is a matrix
    [height,width] = size(input);
    if height==width %满足方阵的条件
        N = height;
        A = zeros(N);
        for i=0:N-1
            if i==0
                c = sqrt(1/N);
            else
                c = sqrt(2/N);
            end
            for j=0:N-1
                A(i+1,j+1) = c*cos(pi*(j+0.5)*i/N);
            end
        end
        output= A*input*A';
    else
    disp('Error:input must be a square matrix !');
    output=0;
end

二、从CTFT到STFT

  我们熟悉的傅里叶变换只能反映出信号在频域的特性，无法在时域内对信号进行分析。为了将时域和频域相联系，短时傅里叶变换(short-time Fourier transform，简称为STFT)便应运而生，其实质是加窗的傅里叶变换。可以去看看参考资料中一篇关于STFT的博客（链接在最后）。
   我拜读之后，简单做了总结，并加了一些理解和补充说明。信号x(t)的短时傅里叶变换定义如下，对比普通的连续傅里叶变换（CTFT），STFT在做傅里叶变换之前对$x(\tau )$先进行加窗，其窗函数的为有限长的$h(\tau )$，当$h(\tau )$变为$h(\tau -t)$时，即相当于对窗函数进行了平移，即可以形象的认为是取出信号在分析时间点 t 附近的一个切片：

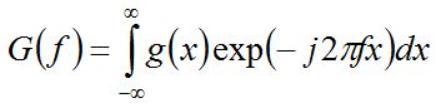
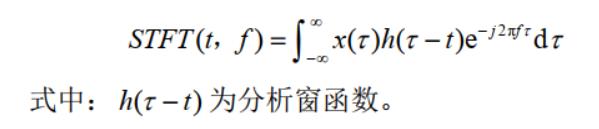
   但是，以上的公式针对的都是连续信号，得到的$f$在频域的取值也是无穷多个，然而在MATLAB仿真的过程中，只能进行数字信号处理，先给出代码，再进行说明。代码如下：

clc,clear;
%% 产生信号
fs = 1000;  % 采样频率1KHz
N=1024;%对应傅里叶变换的点数
t = 0:1/fs:(N-1)/fs;
f1=20;
f2=60;
f3=150;
x=3*cos(2*pi*f1*t)+2*cos(2*pi*f2*t)+5*cos(2*pi*f3*t);%三个正弦信号的叠加
 
%% 短时傅里叶变换
window_length=500;%设置窗口长度，窗口越长时间分辨率越差。
step=1;%每次平移的步长，最小为1，步长越小时间精度越好。
h=hamming(window_length);%设置海明窗的窗长
%wlen-hop代表每次重叠的部分的点数
%F代表频率向量，F的取值为N/2+1；T代表时间向量，step为1时，T的取值为N-wlen+1
[B, F, T, P] = spectrogram(x,h,window_length-step,N,fs);   % B是F行T列的频率峰值，P是对应的能量谱密度
figure;
imagesc(T,F,P);%画图函数
set(gca,'YDir','normal')%让Y轴刻度顺序设置为正常
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('短时傅里叶时频图');

  接下来分析以上代码，调用这个函数之后，返回的向量F代表频率轴，而返回的向量T代表时间轴，而矩阵P则代表了相应的幅度（功率值），P的$size$由向量F和T决定。那么F和T的$size$又是多少呢?我们先看T，由于系统需要满足因果性，我们假定时刻t从0开始，那么一开始窗函数的区间就是从$0$-window_length，假设step为1，即每次向右平移1个，那些就有$N-wlen+1$个时间。再看F，如刚才所说，F的区间是连续的，如何将其离散化，那么需要确定频率分辨率以及频率的分布区间。首先根据奈奎斯特采样定理，采样率$fs$一定的时候，如果我们不想使其发生混叠，信号的频率不会超过$0.5fs$，因此这即为我们考虑的区间上限（下限为0），同时频率分辨率为$\frac{fs}{N}$，即采样率和变换点数一定的时候，频率分辨率就已经确定了，因此，F的size即为$\frac{N}{2}+1$，对应$\frac{N}{2}$个间隔。（也可以这么理解，N点序列作傅里叶变换后得到N点序列，而后面的N/2个点就是前面N/2个点的镜像分量，没有必要考虑）

三、K-L变换与降维思想

  在machine learning中，我们经常需要防止数据的维度过高，而这就需要用到降维的思想。常见的降维有：直接降维，线性降维和非线性降维，而线性降维中常见的方法则是PCA（主成分分析，也称为K-L变换，以下统称用PCA）。
  PCA的核心思想即为将一组线性相关的变量，通过正交变换，变换成一组线性无关的变量，从信号空间理论的角度可以理解为对原始特征空间的重构。在PCA中，有最大投影方差和最小重构距离两种主流思路，最终可推导出相同的结果。事实上，也可以从概率的角度对PCA进行展开，限于篇幅，只给出最终结论，具体请参考AI圣经：PRML。
  对于一组数据集$x_n$，其中的每个$x_n$都在一个$D$维空间中，即研究如何将数据投影到$M<D$的$M$维空间中。具体方法如下：定义$x_n$为样本集合的均值，即$\bar{x}={\sum }_{n=1}^N{x}_n$，而定义数据的协方差矩阵（covariance matrix）：$S=\frac{1}{N}\cdot {\sum }_{n=1}^N(x_n-\bar{x})(x_n-\bar{x}{)}^T$.对矩阵$S$进行特征值分解,对于降维到$M$维空间的情况，则选出$M$个最大的特征值对应的特征向量，即可得到新的$M$维空间中的一组基。
  以上就是PCA的理论部分，但是当涉及到具体实现的时候，我们就会发现，往往原有的空间维数$D$是远远高于样本数量$N$的，就拿我们最常见的图像为例，可能一个图像有100万个像素点，但是样本个数只有大概100个。这样的话，如果直接运行PCA就变的行不通了，因为会遇到$D\cdot D$ 超大矩阵求逆的世界难题，同时，我们会发现这样得到的特征值至少有$D-N+1$个为0，因为N个数据点的线性子空间的维数最多为$N-1$，因此，我们需要采样如下的方法，具体推导可以参考PRML的高维PCA部分，这里给出最终结论：
  1.定义$X$为 D ⋅ N D\\cdot N D⋅N以上是关于常见的变换总结与代码：DCT，STFT，K-L变换等的主要内容，如果未能解决你的问题，请参考以下文章

模式识别与机器学习——4.3离散K-L变换

JPEG压缩原理与DCT离散余弦变换——有实际的数据演示

毕业设计/Matlab系列基于K-L变换的图像压缩matlab实现

K-L变换和 主成分分析PCA

K-L变换

图像隐藏基于DCT(离散余弦变换)与SVD(奇异值分解)域实现自适应嵌入水印含攻击