关于非线性组合模型Geffe的分割攻击实现
Posted 甘薯Yam
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了关于非线性组合模型Geffe的分割攻击实现相关的知识,希望对你有一定的参考价值。
密码学学完序列密码后要做关于Geffe的攻击。。。
看来看去就分割攻击比较好写但是这个LFSR2的级数太高了好像写的有点问题
不管了,快期未考试了
非线性组合模型 G e f f e Geffe Geffe分割攻击
一、非线性组合模型 G e f f e Geffe Geffe发生器的基本介绍
G e f f e Geffe Geffe发生器是1973年 G e f f e Geffe Geffe设计的一个密钥流生成器,具体描述如下:
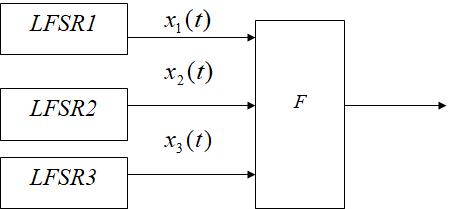
如图所示, G e f f e Geffe Geffe发生器使用了3个 L F S R LFSR LFSR移位寄存器他们以非线性方式组合,其中, L F S R 1 LFSR1 LFSR1和 L F S R 3 LFSR3 LFSR3作为复合器的输入, L F S R 2 LFSR2 LFSR2作为控制复合器。
其中,三个 L F S R LFSR LFSR的反馈多项式分别为:
f 1 ( x ) = x 20 ⊕ x 3 ⊕ 1 f_1(x)=x^20\\oplus x^3\\oplus 1 f1(x)=x20⊕x3⊕1
f 2 ( x ) = x 39 ⊕ x 4 ⊕ 1 f_2(x)=x^39\\oplus x^4\\oplus 1 f2(x)=x39⊕x4⊕1
f 3 ( x ) = x 17 ⊕ x 3 ⊕ 1 f_3(x)=x^17\\oplus x^3\\oplus 1 f3(x)=x17⊕x3⊕1
非线性组合函数
F
F
F为:
g
(
x
1
,
x
2
,
x
3
)
=
x
1
x
2
⊕
(
x
2
⊕
1
)
x
3
=
x
1
,
x
2
=
1
x
3
,
x
2
=
0
g(x_1,x_2,x_3)=x_1x_2\\oplus(x_2\\oplus1)x_3= \\begincases x_1,\\quad x_2=1\\\\ x_3,\\quad x_2=0 \\endcases
g(x1,x2,x3)=x1x2⊕(x2⊕1)x3=x1,x2=1x3,x2=0
二、非线性组合模型 G e f f e Geffe Geffe的初始化过程
(1)密钥 K = ( k 63 , … , k 0 ) K=(k_63,…,k_0) K=(k63,…,k0)按照如下方式填充:
先将密钥重复链接,得到76比特密钥 K ’ K’ K’
K ’ = ( k 11 , … , k 1 , k 0 , k 63 , … , k 0 ) K’=(k_11,…, k_1,k_0,k_63,…,k_0) K’=(k11,…,k1,k0,k63,…,k0)
将 K ’ K’ K’由低位到高位按照从右到左的顺序依次填入 L F S R 1 LFSR1 LFSR1、 L F S R 2 LFSR2 LFSR2和 L F S R 3 LFSR3 LFSR3。
2)按照密钥流生成方式空转100个时刻
将此时 L F S R LFSR LFSR的内部状态做为密钥流生成的初态。
三、非线性组合模型 G e f f e Geffe Geffe分割攻击流程
1.穷举 L F S R 2 LFSR2 LFSR2的初态
2.获得关于 L F S R 1 LFSR1 LFSR1和 L F S R 3 LFSR3 LFSR3初态的线性方程;
3.解方程得到初态
4.根据前100个时刻的乱数,验证初态是否正确
四、分割攻击具体实现代码及注释
1.定义密钥流 K K K的值并将 K K K填充到三个 L F S R LFSR LFSR的初态中
string K="1010010010000101010100101010110101101100100111001011010001110011";//K为初始密钥
string s1,s2,s3;//s1,s2,s3中分别为LFSR1 2 3的初始填充
s1="11001011010001110011";
s2="100100001010101001010101101011011001001";
s3="01000111001110100";
2.将 L F S R LFSR LFSR空转100个时刻并记录下产生的密钥流
void LFSR_f1(int l_xunhuan,string chutai)//LFSR1的实现代码,其中l_xunhuan为循环轮数,chutai为LFSR的初态
bitset<20>f1(chutai);//初态赋值
//cout<<f1.to_string();
for(int i=1;i<=l_xunhuan;i++)//移位寄存
int j=f1[0]^f1[17] ;
len_f1++;
//string s_out = f1.to_string();
f1_out += '0'+j;
f1.operator>>=(1);
f1[19]=j;
void LFSR_f2(int l_xunhuan,string chutai)//LFSR2的实现代码,其中l_xunhuan为循环轮数,chutai为LFSR的初态
bitset<39>f2(chutai);//初态赋值
//cout<<f2.to_string();
for(int i=1;i<=l_xunhuan;i++)//移位寄存
int j=f2[0]^f2[35] ;
len_f2++;
//string s_out = f2.to_string();
f2_out += '0'+j;
f2.operator>>=(1);
f2[38]=j;
void LFSR_f3(int l_xunhuan,string chutai)//LFSR2的实现代码,其中l_xunhuan为循环轮数,chutai为LFSR的初态
bitset<17>f3(chutai);//初态赋值
//cout<<f3.to_string();
for(int i=1;i<=l_xunhuan;i++)//移位寄存
int j=f3[0]^f3[14] ;
len_f3++;
//cout<<i<<endl;
//cout<<"f3_out--->"<<f3_out<<endl;
//string s_out = f3.to_string();
f3_out += j+'0' ;
f3.operator>>=(1);
f3[16]=j;
//此为主函数的调用语句
LFSR_f1(100,s1);
LFSR_f2(100,s2);
LFSR_f3(100,s3);
3.根据 L F S R 2 LFSR2 LFSR2的值来决定最后输出密钥流的每一位取 L F S R 1 LFSR1 LFSR1还是取 L F S R 3 LFSR3 LFSR3的值
string f0_out;//为最终输出密钥流
for(int i=0;i<100;i++)
if(f2_out[i]=='1') f0_out+=f1_out[i];
else f0_out+=f3_out[i];
4.枚举 L F S R 2 LFSR2 LFSR2的初态
int cnt =0;
int x_len = 1<<39;
for(int i=0;i<x_len;i++)
//中间流程由后面具体解释
5.根据 L F S R 2 LFSR2 LFSR2的初态,推算出 L F S R 1 LFSR1 LFSR1和 L F S R 3 LFSR3 LFSR3的初态
int cnt =0;
int x_len = 1<<39;
for(int i=0;i<x_len;i