蓝桥杯ACMLeetCode 面试,你不得不学的数学基础
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯ACMLeetCode 面试,你不得不学的数学基础相关的知识,希望对你有一定的参考价值。
前言
算法是什么?数学是什么?算法中的数学又是什么?这篇文章,让我来为大家介绍下法中的数学基础。
数学可以说是算法的基石,所谓万丈高楼平地起,如若根基不稳,那么再高的楼,也只是豆腐渣工程,随时都有塌陷的可能。所以数学之于算法,可谓 非常重要。
我们在刷编程题时,需要掌握的数学基础,其实只是数学的冰山一角,所以大可不必心生畏惧。因为反正也学不完,能学一点是一点,只要把我整理的每个知识点,都刷上三到五道题,掌握其精髓,以后遇到其它题目,能够举一反三,触类旁通,别的就不要奢望太多啦,不可能每个题都会做的啦。
算法中的数学基础总结
《算法中的数学基础总结》视频完整版
算法中的数学,大致可以分为以下几个模块:
我会先进行简单概述,然后对每个模块,讲解几道经典的例题,让你对算法中的数学,有一个初步的了解:
文章目录
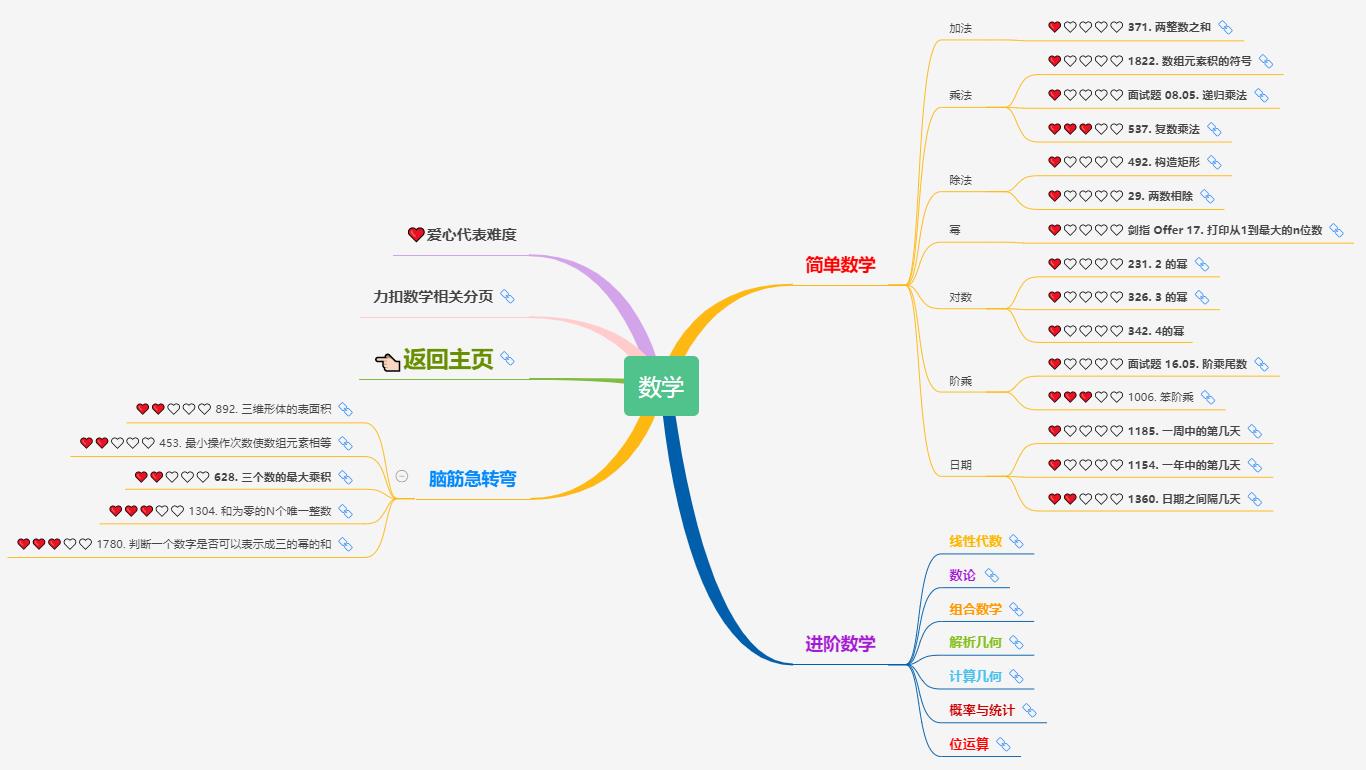
一、简单数学
1、教程总览
简单数学就是初中高中大学学到的加减乘除四则运算,数列、函数、幂、对数、阶乘、求导、极限、求积分 等等。相关的内容参考如下:
2、例题讲解
其实也没那么复杂啦,我们先来看一道例题。
【例题1】给定一个数组,求所有元素的乘积的符号,如果最终答案是负的返回-1,如果最终答案是正的返回1,如果答案是0返回0。
3、算法分析
仔细分析一下这道题目,如果将所有数都乘起来,再判断正负,在C语言中势必是不可行的,答案一定会超过 int32甚至 int64。
但是我们发现,一个数如果是 -100 和 -1,对符号位的贡献是完全一样的,所以只需要看有多少个负数,就能够判断最后乘积的符号了。
4、源码详解
int arraySign(int* nums, int numsSize)
int i; // (1)
int prod = 1; // (2)
for(i = 0; i < numsSize; ++i) // (3)
if(nums[i] == 0) // (4)
return 0;
else if(nums[i] < 0) // (5)
prod = -prod;
return prod; // (6)
力扣给我们提供了这么一个函数int arraySign(int* nums, int numsSize)。
(1)首先我们定义一个循环变量;
(2)然后用一个变量记录所有数乘积的符号;
(3)对所有数进行一个依次遍历;
(4)如果数组中有 0 的存在,那么直接返回 0即可,因为所有数乘上 0 都是 0 嘛;
(5)如果当前的数是负数,那么我们进行一次符号位的翻转;
(6)最后返回这个记录的符号即可;
5、更多例题
各种例题的题目链接,统一在文末给出。
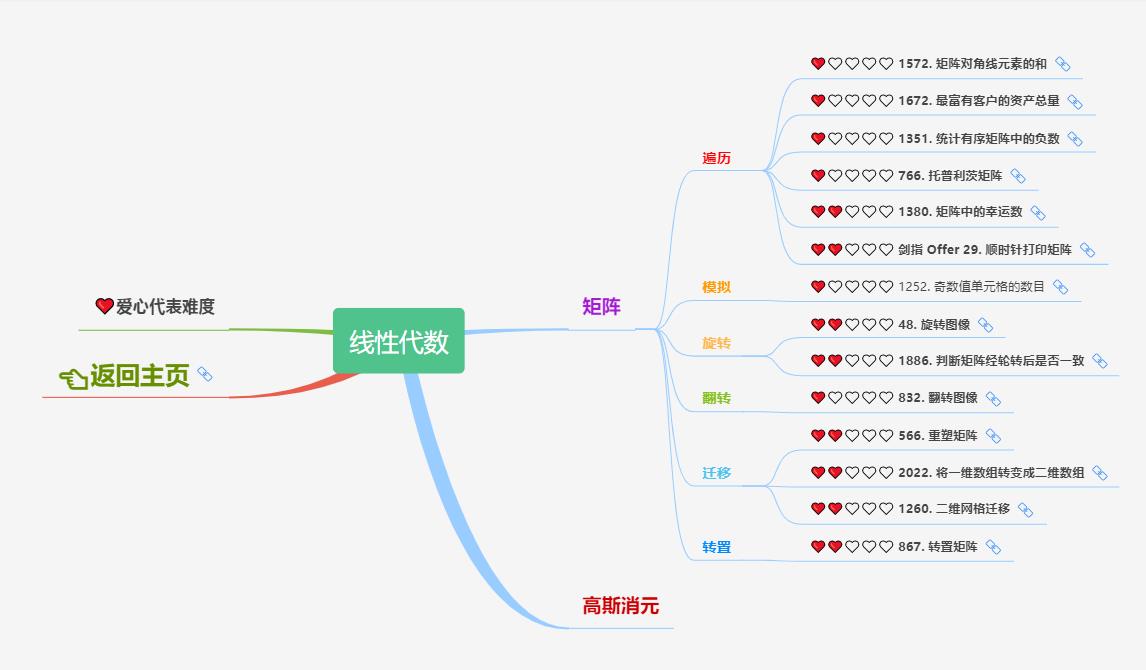
二、线性代数
1、教程总览
线性代数在刷题中,遇到的最多的概念就是矩阵。有矩阵的遍历、翻转、旋转、转置等等。当然还有多元一次方程组求解,可以采用高斯消元。
2、例题讲解
我们先来看一道矩阵遍历的题
【例题2】给定一个正方形矩阵,求它的主对角和副对角线的元素的和。
3、算法分析
思路很简单,直接遍历主对角线和副对角线,然后逐个求和即可。唯一需要注意的是:当矩阵行列是奇数的时候,中心的元素会被两条对角线计算两次,需要把它减去。
4、源码详解
我们来写一下代码:
int diagonalSum(int** mat, int matSize, int* matColSize)
int r = matSize;
int c = r; // (1)
int i; // (2)
int ans = 0; // (3)
for(i = 0; i < r; ++i)
ans += mat[i][i]; // (4)
for(i = 0; i < r; ++i)
ans += mat[i][r-i-1]; // (5)
if(r % 2 == 1)
ans -= mat[r/2][r/2]; // (6)
return ans; // (7)
(1)由于这个矩阵是一个正方形,所以它的行和列都是 matSize;
(2)然后定义一个循环变量;
(3)以及一个值代表所有对角线元素的和;
(4)先统计主对角线的和;
(5)再统计副对角线的和;
(6)如果行列为奇数,则减去中间的那个元素,因为它被多计算了一次;
(7)最后返回求和结果即可;
5、更多例题
各种例题的题目链接,统一在文末给出。
三、组合数学
1、教程总览
组合数学在刷题中的应用,主要有以下几个内容:
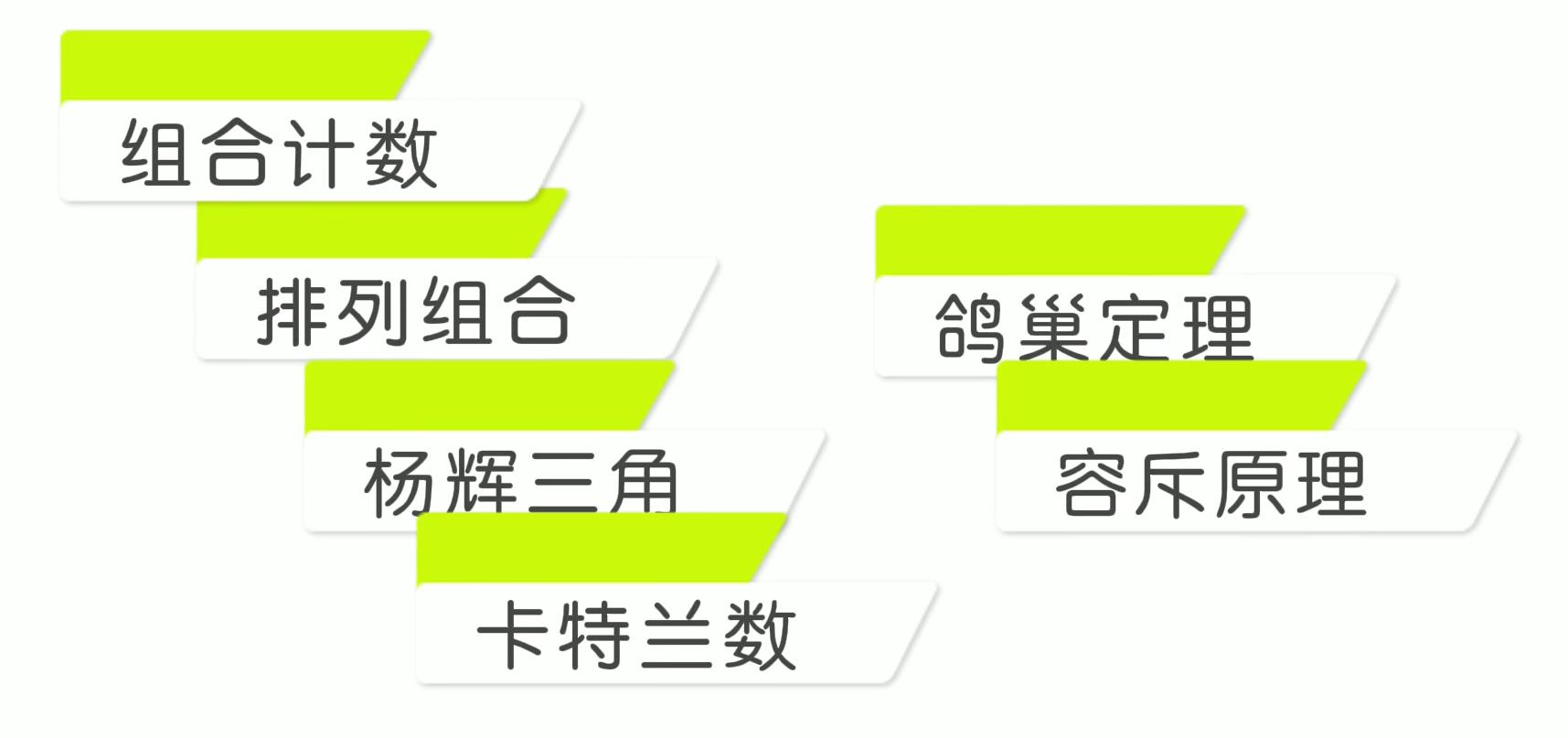
这些概念都比较简单啦,务必全部掌握,当然掌握并不代表学会,还是要多刷题实践,毕竟实践是检验真理的唯一标准。介于时间问题,我来简单介绍一个组合计数问题。
2、例题讲解
【例题3】给你一个非负整数 n ( n ≤ 1 0 6 ) n(n \\le 10^6) n(n≤106) ,如果当前数字是偶数,你需要把它除以 2;如果当前数字是奇数,你需要把它减去 1,反复操作,请你返回将它变成 0 所需要的步数。
3、算法分析
那么,我们用
f
(
n
)
f(n)
f(n) 表示
n
n
n 变成 0 需要的步数。很明显,
f
(
0
)
=
0
f(0) = 0
f(0)=0。当
n
n
n 为奇数的时候,
f
(
n
)
=
f
(
n
−
1
)
+
1
f(n) = f(n-1) + 1
f(n)=f(n−1)+1 当
n
n
n 为偶数的时候,
f
(
n
)
=
f
(
n
2
)
+
1
f(n) = f(\\frac n2) + 1
f(n)=f(2n)+1,这时候你看,我们就可以列出一个递推方程:
f
(
n
)
=
0
n
=
0
f
(
n
−
1
)
+
1
n
为
奇
数
f
(
n
/
2
)
+
1
n
为
偶
数
f(n) = \\begincases0 & n=0\\\\ f(n-1) + 1& n为奇数\\\\ f(n/2) + 1& n为偶数\\\\ \\endcases
f(n)=⎩⎪⎨⎪⎧0f(n−1)+1f(n/2)+1n=0n为奇数n为偶数
我们把它理解成一个数列,并且用一个 1000000 的数组来存储这数列。
4、源码详解
看看代码要怎么写:
int f[1000001]; // (1)
int numberOfSteps(int n)
int i;
f[0] = 0; // (2)
for(i = 1; i <= n; ++i) // (3)
if(i % 2 == 1) // (4)
f[i] = f[i-1] + 1; // (5)
else
f[i] = f[i/2] + 1; // (6)
return f[n]; // (7)
(1)首先定义一个全局数组 f[1000001]用来存储结果;
(2)定义好最初始的情况f[0] = 0;
(3)从 1 遍历到
n
n
n;
(4)每次根据奇偶性计算f[i]的值;
(5)奇数的时候是这样的;
(6)偶数的时候是这样的;
(7)每次计算过程是
O
(
1
)
O(1)
O(1) 的,所以总的时间复杂度为
O
(
n
)
O(n)
O(n),一遍计算完毕结果就出来啦;
5、更多例题
这时候我们发现,在写代码之前一定要把问题先想清楚,抽象成一个具体的数学问题。一旦想清楚以后,写代码就会轻松许多,当然啦,这只是一个简单的例题,更多的例题可以参考我整理的组合数学题集。
各种例题的题目链接,统一在文末给出。
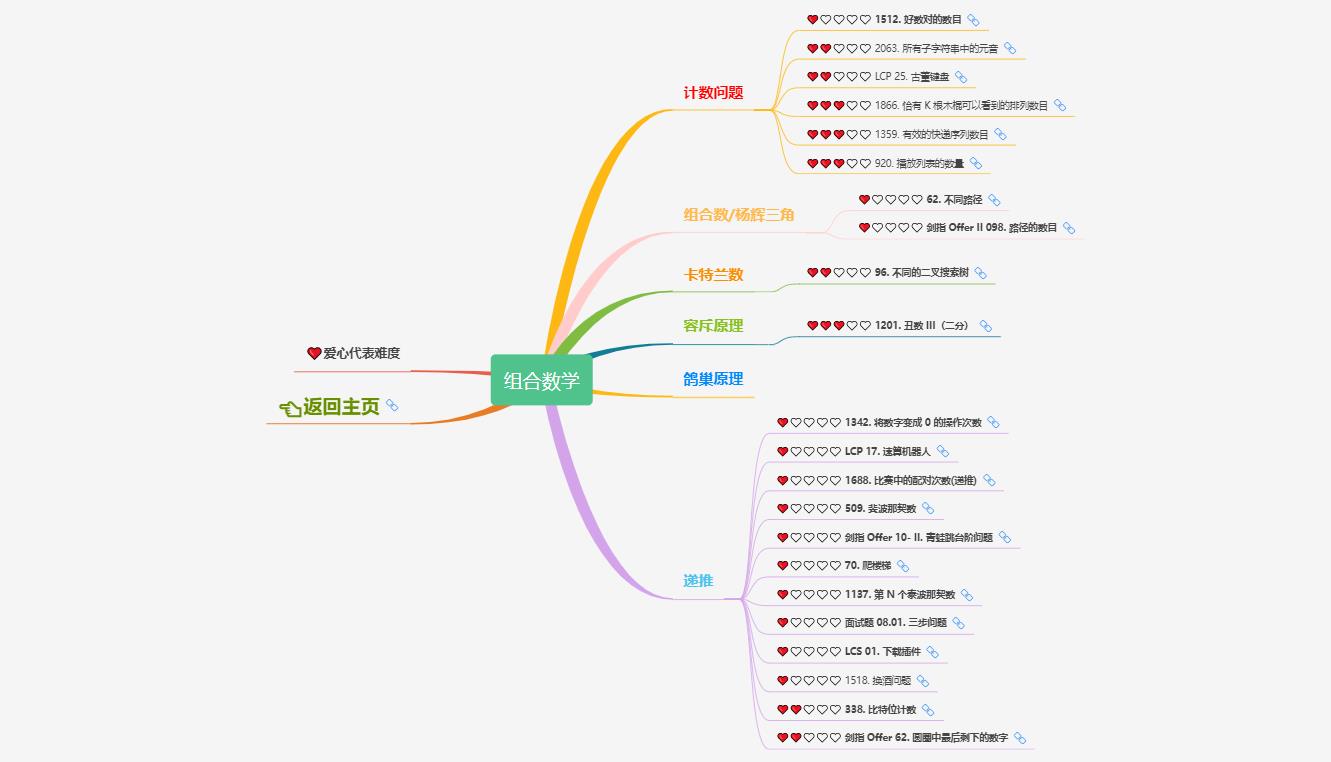
四、初等数论
1、教程总览
初等数论是一个很重要的数学分支,主要研究的是整数的性质。主要有以下几块内容:

2、例题讲解
我们先来通过一道简单的例题,了解一下数论是解决什么问题的。
【例题4】给你两个正整数 n n n 和 k k k。如果正整数 i i i 满足 n n n 是 i i i 的倍数, 那么我们就说正整数 i i i 是整数 n n n 的因子。考虑整数 n n n 的所有因子,将它们 升序排列 。请你返回第 k k k 个因子。如果 n n n 的因子数少于 k k k ,请你返回 -1 。
3、算法分析
首先如果一个数是 n n n 的因子,则必然比它小,由此可知,必然最多只有 n n n 个因子,实际上肯定更少。所以我们可以枚举所有可能的因子,并且进行整除性判定,如果能够整除 n n n,则代表它是 n n n 的一个因子,并且进行计数,当计数到 k k k 的时候,就代表它是第 k k k 个因子。
4、源码详解
我们来看下代码怎么写
int kthFactor(int n, int k)
int i; // (1)
int cnt = 0; // (2)
for(i = 1; i <= n; ++i) // (3)
if(n % i == 0) // (4)
++cnt; // (5)
if(cnt == k) // (6)
return i;
return -1; // (7)
(1)首先定义一个循环变量;
(2)再定义一个计数器;
(3)然后从 1 到
n
n
n 枚举因子
i
i
i;
(4)如果发现
n
n
n 是
i
i
i 的倍数,则
i
i
i 作为一个因子;
(5)并且计数器自增;
(6)等计数器到
k
k
k 的时候,
i
i
i 就是第
k
k
k 个因子,直接返回即可;
(7)当然如果没有找到,按照题目要求,返回 -1 即可;
5、更多例题
当然啦~数论博大精深,三言两语又怎能讲完,这只是一个简单的例题。更多的例题可以参考我整理的数论题集。
各种例题的题目链接,统一在文末给出。
五、概率论
1、教程总览
概率论主要有 概率、期望 等等问题。
2、题集整理
各种例题的题目链接,统一在文末给出。
六、几何
1、教程总览
几何问题大致可以分为:解析几何 和 计算几何。解析几何是利用解析式研究几何对象解决几何问题的方法。一般就是点线面方程联立,且拥有一个坐标系。计算几何相比解析几何,区别在于:它是不需要考虑坐标系的,并且它能够利用叉乘和点乘,尽量避免运用除法,而最大限度减少精度误差。
2、例题讲解
我们来看一道简单的几何题:
【例题5】给定由一些正数组成的数组 A,返回由其中三个长度组成的面积不为零的三角形的最大周长,如果不能形成任何面积不为零的三角形则返回 0。
3、算法分析
假设所有边有序排列以后,三条边
l
<
m
<
n
l < m < n
l<m<n,其中
n
n
n 是最大的那条边。
那么如果
l
+
m
>
n
l + m > n
l+m>n,则它们能够组成一个三角形,最大周长就是
l
+
m
+
n
l + m + n
l+m+n。并且能够让上面不等式成立且
l
+
m
+
n
l + m + n
l+m+n 最大的情况,一定是
