优化算法帝国主义竞争优化算法（ICA）含Matlab源码 1635期

Posted 2022-01-15 紫极神光

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】帝国主义竞争优化算法（ICA）【含Matlab源码 1635期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、帝国主义竞争优化算法简介

帝国主义算法流程描述如下:
1)初始化帝国主义竞争算法的参数:Npop,Nimp2)随机生成Npop作为国家的人口数量。选择Nimp最好的国家作为帝国并根据他们的能力规定他们的殖民地数量;
3)如果终止条件未得到满足,则重复下列步骤;
4)内部位置交换;
5)帝国主义竞争;
6)淘汰弱小的帝国;
7)保留最终剩余的帝国,其适应度取值作为最优解。
流程图如图1所示。

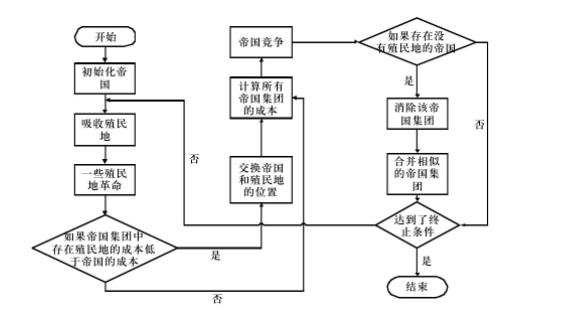
三、部分源代码

close all
clc; clear
%% Problem Statement
ProblemParams.CostFuncName = 'BenchmarkFunction';    % You should state the name of your cost function here.
ProblemParams.CostFuncExtraParams = 6;
ProblemParams.NPar = 30;                           % Number of optimization variables of your objective function. "NPar" is the dimention of the optimization problem.
ProblemParams.VarMin = -6;                         % Lower limit of the optimization parameters. You can state the limit in two ways. 1)   2)
ProblemParams.VarMax = 6;                       % Lower limit of the optimization parameters. You can state the limit in two ways. 1)   2)

% Modifying the size of VarMin and VarMax to have a general form
if numel(ProblemParams.VarMin)==1
    ProblemParams.VarMin=repmat(ProblemParams.VarMin,1,ProblemParams.NPar);
    ProblemParams.VarMax=repmat(ProblemParams.VarMax,1,ProblemParams.NPar);
end

ProblemParams.SearchSpaceSize = ProblemParams.VarMax - ProblemParams.VarMin;

%% Algorithmic Parameter Setting
AlgorithmParams.NumOfCountries = 200;               % Number of initial countries.
AlgorithmParams.NumOfInitialImperialists = 8;      % Number of Initial Imperialists.
AlgorithmParams.NumOfAllColonies = AlgorithmParams.NumOfCountries - AlgorithmParams.NumOfInitialImperialists;
AlgorithmParams.NumOfDecades = 2000;
AlgorithmParams.RevolutionRate = 0.3;               % Revolution is the process in which the socio-political characteristics of a country change suddenly.
AlgorithmParams.AssimilationCoefficient = 2;        % In the original paper assimilation coefficient is shown by "beta".
AlgorithmParams.AssimilationAngleCoefficient = .5;  % In the original paper assimilation angle coefficient is shown by "gama".
AlgorithmParams.Zeta = 0.02;                        % Total Cost of Empire = Cost of Imperialist + Zeta * mean(Cost of All Colonies);
AlgorithmParams.DampRatio = 0.99;
AlgorithmParams.StopIfJustOneEmpire = false;         % Use "true" to stop the algorithm when just one empire is remaining. Use "false" to continue the algorithm.
AlgorithmParams.UnitingThreshold = 0.02;            % The percent of Search Space Size, which enables the uniting process of two Empires.

zarib = 1.05;                       % **** Zarib is used to prevent the weakest impire to have a probability equal to zero
alpha = 0.1;                        % **** alpha is a number in the interval of [0 1] but alpha<<1. alpha denotes the importance of mean minimum compare to the global mimimum.

%% Display Setting
DisplayParams.PlotEmpires = false;    % "true" to plot. "false" to cancel ploting.
if DisplayParams.PlotEmpires
    DisplayParams.EmpiresFigureHandle = figure('Name','Plot of Empires','NumberTitle','off');
    DisplayParams.EmpiresAxisHandle = axes;
end

DisplayParams.PlotCost = true;    % "true" to plot. "false"
if DisplayParams.PlotCost
    DisplayParams.CostFigureHandle = figure('Name','Plot of Minimum and Mean Costs','NumberTitle','off');
    DisplayParams.CostAxisHandle = axes; 
end

ColorMatrix = [1   0   0  ; 0 1   0    ; 0   0 1    ; 1   1   0  ; 1   0 1    ; 0 1   1    ; 1 1 1       ;
               0.5 0.5 0.5; 0 0.5 0.5  ; 0.5 0 0.5  ; 0.5 0.5 0  ; 0.5 0 0    ; 0 0.5 0    ; 0 0 0.5     ;
               1   0.5 1  ; 0.1*[1 1 1]; 0.2*[1 1 1]; 0.3*[1 1 1]; 0.4*[1 1 1]; 0.5*[1 1 1]; 0.6*[1 1 1]];
DisplayParams.ColorMatrix = [ColorMatrix ; sqrt(ColorMatrix)];

DisplayParams.AxisMargin.Min = ProblemParams.VarMin;
DisplayParams.AxisMargin.Max = ProblemParams.VarMax;

%% Creation of Initial Empires
InitialCountries = GenerateNewCountry(AlgorithmParams.NumOfCountries , ProblemParams);

% Calculates the cost of each country. The less the cost is, the more is the power.
if isempty(ProblemParams.CostFuncExtraParams)
    InitialCost = feval(ProblemParams.CostFuncName,InitialCountries);    
else
    InitialCost = feval(ProblemParams.CostFuncName,InitialCountries,ProblemParams.CostFuncExtraParams);
end
[InitialCost,SortInd] = sort(InitialCost);                          % Sort the cost in assending order. The best countries will be in higher places
InitialCountries = InitialCountries(SortInd,:);                     % Sort the population with respect to their cost.

Empires = CreateInitialEmpires(InitialCountries,InitialCost,AlgorithmParams, ProblemParams);

%% Main Loop
MinimumCost = repmat(nan,AlgorithmParams.NumOfDecades,1);
MeanCost = repmat(nan,AlgorithmParams.NumOfDecades,1);

if DisplayParams.PlotCost
    axes(DisplayParams.CostAxisHandle);
    if any(findall(0)==DisplayParams.CostFigureHandle)
        h_MinCostPlot=plot(MinimumCost,'r','LineWidth',1.5,'YDataSource','MinimumCost');
        hold on;
        h_MeanCostPlot=plot(MeanCost,'k:','LineWidth',1.5,'YDataSource','MeanCost');
        hold off;
        pause(0.05);
    end
end

for Decade = 1:AlgorithmParams.NumOfDecades
    AlgorithmParams.RevolutionRate = AlgorithmParams.DampRatio * AlgorithmParams.RevolutionRate;

    Remained = AlgorithmParams.NumOfDecades - Decade
    for ii = 1:numel(Empires)
        %% Assimilation;  Movement of Colonies Toward Imperialists (Assimilation Policy)
        Empires(ii) = AssimilateColonies(Empires(ii),AlgorithmParams,ProblemParams);

        %% Revolution;  A Sudden Change in the Socio-Political Characteristics
        Empires(ii) = RevolveColonies(Empires(ii),AlgorithmParams,ProblemParams);
        
        %% New Cost Evaluation
        if isempty(ProblemParams.CostFuncExtraParams)
            Empires(ii).ColoniesCost = feval(ProblemParams.CostFuncName,Empires(ii).ColoniesPosition);
        else
            Empires(ii).ColoniesCost = feval(ProblemParams.CostFuncName,Empires(ii).ColoniesPosition,ProblemParams.CostFuncExtraParams);
        end

        %% Empire Possession  (****** Power Possession, Empire Possession)
        Empires(ii) = PossesEmpire(Empires(ii));
        
        %% Computation of Total Cost for Empires
        Empires(ii).TotalCost = Empires(ii).ImperialistCost + AlgorithmParams.Zeta * mean(Empires(ii).ColoniesCost);
    
    end
    
    %% Uniting Similiar Empires
    Empires = UniteSimilarEmpires(Empires,AlgorithmParams,ProblemParams);

    %% Imperialistic Competition
    Empires = ImperialisticCompetition(Empires);
    
    if numel(Empires) == 1 && AlgorithmParams.StopIfJustOneEmpire
        break
    end

    %% Displaying the Results
    DisplayEmpires(Empires,AlgorithmParams,ProblemParams,DisplayParams);
    
    ImerialistCosts = [Empires.ImperialistCost];
    MinimumCost(Decade) = min(ImerialistCosts);
    MeanCost(Decade) = mean(ImerialistCosts);

    if DisplayParams.PlotCost
        refreshdata(h_MinCostPlot);
        refreshdata(h_MeanCostPlot);
        drawnow;
        pause(0.01);
    end

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]陈志楚,李聪,张超勇.基于帝国主义竞争算法的切削参数优化[J].制造业自动化. 2012,34(24)