剑指 Offer 68 - I. 二叉搜索树的最近公共祖先(二叉搜索树性质迭代递归)
Posted --believe
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了剑指 Offer 68 - I. 二叉搜索树的最近公共祖先(二叉搜索树性质迭代递归)相关的知识,希望对你有一定的参考价值。
一、题目
剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
题目描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
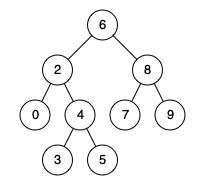
示例1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
示例2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
二、分析
这道题是一道leetcode简单题。但是一拿到题的时候有点蒙圈。题目条件限定二叉搜索树,我们就要好好理解到二叉搜索树的概念,左子树小于右子树,更要会灵活应用。
对于此题,我们要思考二叉搜索树中任意两节点p,q的最近公共祖先Ancestor。他们之间有什么特性?
很容易发现 p、q一定是parent的左右子树(将p、q任一等于Ancestor作为特例,先不考虑)。由二叉搜索树中又可以得到左子树<Ancestor<右子树。我们根据此性质来搜索二插树,遍历的每个节点设为root
有下面三种情况:
- p,q都小于root,那么p,q一定在root左子树上,Ancestor也在root的左子树上,因此root=root.left,往左边搜索
- p,q都大于root,那么p,q一定在root右子树上,Ancestor也在root的右子树上,因此root=root.left,往右边搜索
- p,q一大一小(相对于root)或者有任意节点等于root,那么Ancestor=root
迭代、递归都可以实现上面的方法,分析想到怎么利用搜索树的性质比较难,只要将这三类分类好后,代码实现不成问题。
三、代码
方法1 迭代
/*
* 题目:剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
* 描述:给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
* 实现:迭代。根据二搜索树定义来做。
* 复杂度:时间O(N):二叉树退化成链表,需要O(N)
* 空间 O(1):常数辅助空间
*/
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
while (true)
if (p->val < root->val && q->val < root->val) root = root->left;
else if (p->val > root->val && q->val > root->val) root = root->right;
else break;
return root;
方法2 递归
/*
* 题目:剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
* 描述:给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
* 实现:递归(根据二叉搜索树定义来做)
* 复杂度:时间O(N):二叉树退化成链表,需要O(N)
* 空间 O(N):线性辅助空间
*/
TreeNode* lowestCommonAncestorA(TreeNode* root, TreeNode* p, TreeNode* q)
if (p->val < root->val && q->val < root->val) return lowestCommonAncestorA(root->left, p, q);
else if (p->val > root->val && q->val > root->val) return lowestCommonAncestorA(root->right, p, q);
else return root;
四、总结
二叉搜索树的性质我们都知道,但是灵活应用性质我们需要积累经验。
这道题告诉我们二叉搜索树任意两个节点的最小公共祖先节点可以判断p,q位列root节点的左右子树来快速得到。
索树的性质我们都知道,但是灵活应用性质我们需要积累经验。
这道题告诉我们二叉搜索树任意两个节点的最小公共祖先节点可以判断p,q位列root节点的左右子树来快速得到。
以上是关于剑指 Offer 68 - I. 二叉搜索树的最近公共祖先(二叉搜索树性质迭代递归)的主要内容,如果未能解决你的问题,请参考以下文章