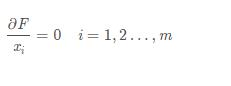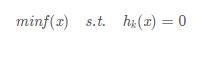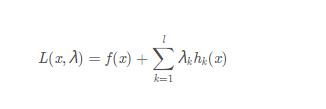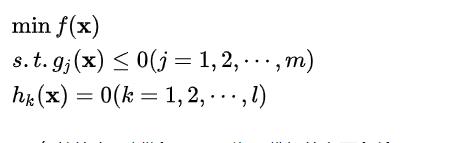数学知识笔记:拉格朗日乘子
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学知识笔记:拉格朗日乘子相关的知识,希望对你有一定的参考价值。
1 中心思想
极值点处,函数和约束条件一定相切,梯度一定共线(同向or反向)
2 无约束优化问题
比如我们希望求解 min/max F(x),那么我们可以直接对所有m个变量求偏导,令偏导等于0。
这时候联立出来的点就可能是极值点
注意这里是可能,因为偏导等于0只是极值点的必要条件,并不是它的充分条件。(所以在求出可能的极值之后,需要带入原函数,检查一下是否在原函数中比周围的点都要小)
但从另一个角度讲,不满足偏导数等于0的点,肯定不是极值点。
3 等式约束优化问题
比如我们现在的目标函数为 f(x),约束条件为h(x)
那么问题为:
此时我们构建拉格朗日函数
我们令其关于λ以及x的偏导数为0
4 不等式约束问题(KKT)
我们将约束条件扩展成如下:
如何求解最优值?我们可以使用KKT条件进行求解:
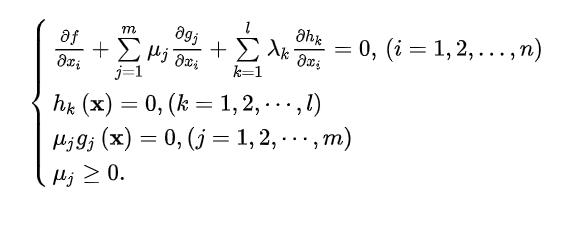
参考资料 拉格朗日乘子法详解(Lagrange multiplier)_wulimmya的博客-CSDN博客_拉格朗日乘子
以上是关于数学知识笔记:拉格朗日乘子的主要内容,如果未能解决你的问题,请参考以下文章