数据结构与算法之深入解析“石子游戏”的求解思路与算法示例

Posted 2022-01-14 Forever_wj

一、题目描述

• Alice 和 Bob 用几堆石子在做游戏，一共有偶数堆石子，排成一行；每堆都有正整数颗石子，数目为 piles[i] 。
• 游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ，所以没有平局。
• Alice 和 Bob 轮流进行，Alice 先开始，每回合玩家从行的开始或结束处取走整堆石头，这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜 。
• 假设 Alice 和 Bob 都发挥出最佳水平，当 Alice 赢得比赛时返回 true ，当 Bob 赢得比赛时返回 false。
• 示例 1：

输入：piles = [5,3,4,5]
输出：true
解释：
Alice 先开始，只能拿前 5 颗或后 5 颗石子。
假设他取了前 5 颗，这一行就变成了 [3,4,5]。
如果 Bob 拿走前 3 颗，那么剩下的是 [4,5]，Alice 拿走后 5 颗赢得 10 分。
如果 Bob 拿走后 5 颗，那么剩下的是 [3,4]，Alice 拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对 Alice 来说是一个胜利的举动，所以返回 true。

• 示例 2：

输入：piles = [3,7,2,3]
输出：true

二、求解算法

① 数学

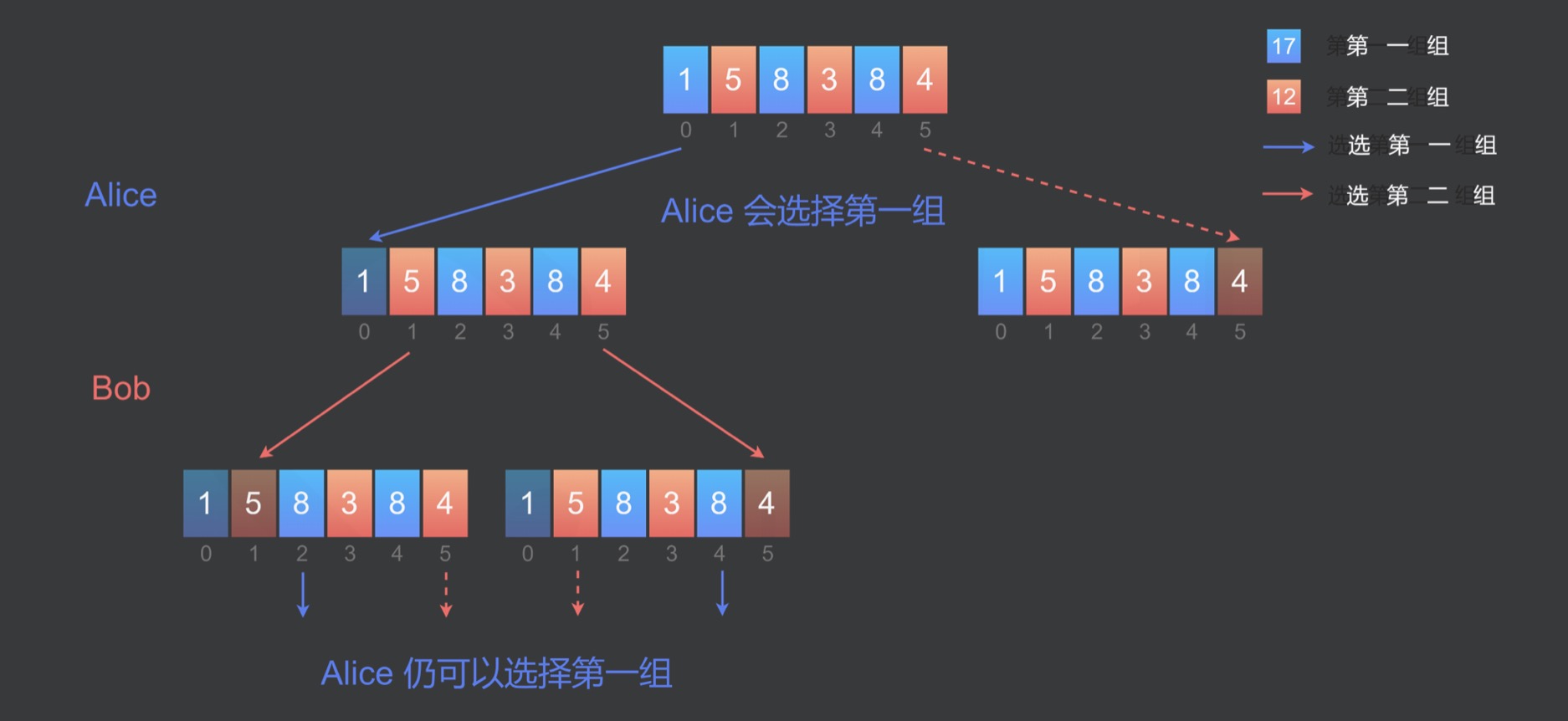
• 假设有 n 堆石子，n 是偶数，则每堆石子的下标从 0 到 n−1，根据下标将 n 堆石子分成两组，每组有 n/2 堆石子，下标为偶数的石子堆属于第一组，下标为奇数的石子堆属于第二组。
• 初始时，行的开始处的石子堆位于下标 0，属于第一组，行的结束处的石子堆位于下标 n−1，属于第二组，因此作为先手的 Alice 可以自由选择取走第一组的一堆石子或者第二组的一堆石子。如果 Alice 取走第一组的一堆石子，则剩下的部分在行的开始处和结束处的石子堆都属于第二组，因此 Bob 只能取走第二组的一堆石子。如果 Alice 取走第二组的一堆石子，则剩下的部分在行的开始处和结束处的石子堆都属于第一组，因此 Bob 只能取走第一组的一堆石子。无论 Bob 取走的是开始处还是结束处的一堆石子，剩下的部分在行的开始处和结束处的石子堆一定是属于不同组的，因此轮到 Alice 取走石子时，Alice 又可以在两组石子之间进行自由选择。
• 根据上述分析可知，作为先手的 Alice 可以在第一次取走石子时就决定取走哪一组的石子，并全程取走同一组的石子。既然如此，Alice 是否有必胜策略？答案是肯定的，将石子分成两组之后，可以计算出每一组的石子数量，同时知道哪一组的石子数量更多。Alice 只要选择取走数量更多的一组石子即可，因此，Alice 总是可以赢得比赛。

• Java 示例：

class Solution 
    public boolean stoneGame(int[] piles) 
        return true;
    

② 记忆化递归

• 每一轮玩家从行的开始或结束处取走整堆石头，决定了这个问题的无后效性，因此可以使用「动态规划」求解。
• 题目中很关键的信息或条件：
• • 每一次的选择：每次只能取一堆石子，或者在开始处，或者在结尾处；
• • 游戏终止条件：最后一堆石子被取走；
• • 获胜条件：哪一个玩家获得的石子总数最多。
• 如下图所示，采用这样一种计算的方式，当前自己做出选择的时候，得分为正，留给对方做选择的时候，相对于自己而言，得分为负，①②③④ 在图后面中有说明是如何做出最优选择的：
• • 绿色框表示当前 Alex 做出选择；
• • 蓝色框表示当前 Lee 做出选择。

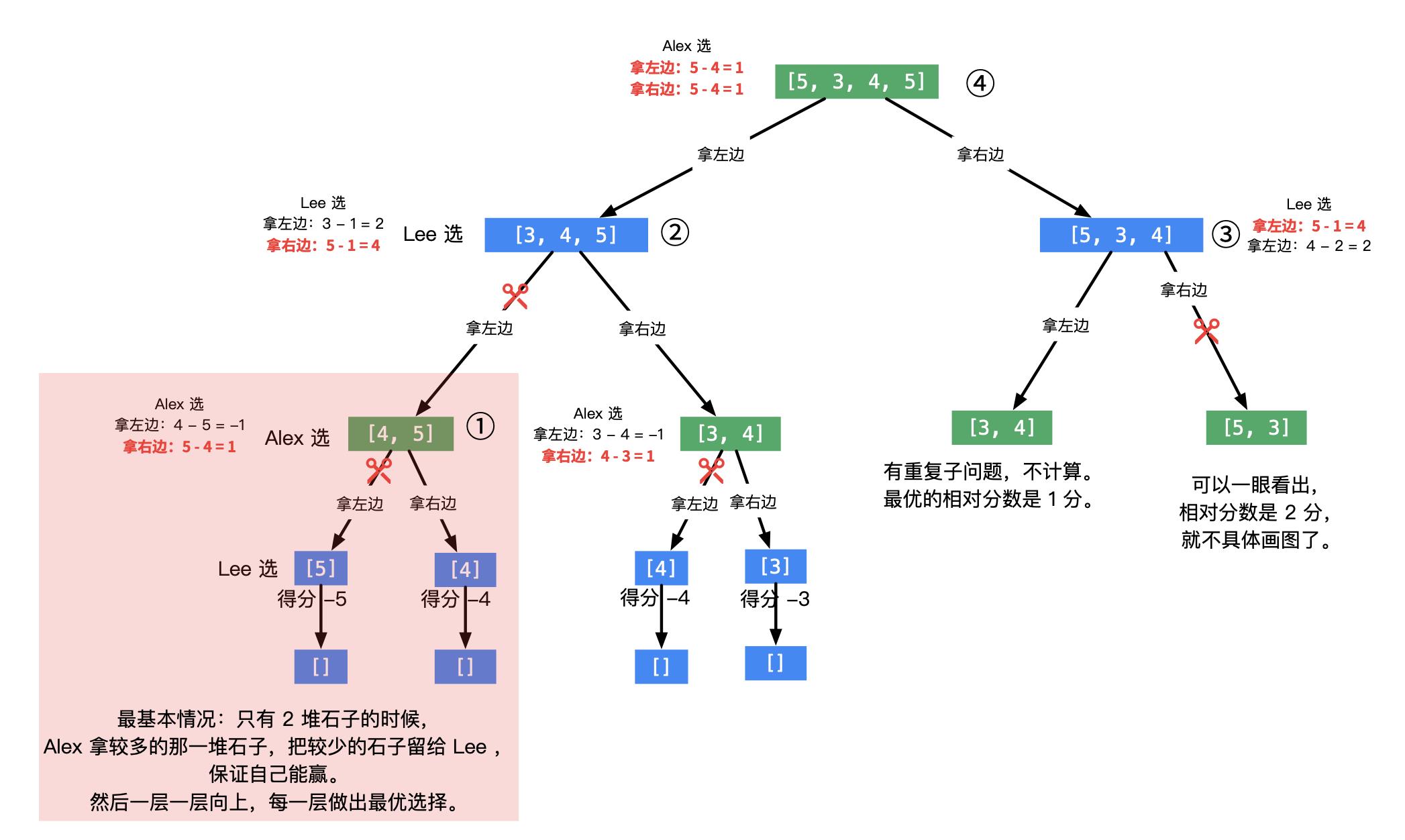
• 说明如下：
• • ① 先从只有 2 堆石子的时候开始考虑，当前做出选择的人，一定会选一个较大的，好让对方拿较少的；
• • ② 再考虑这里，Lee 不管是选择 5 还是 3 ，在下一轮 Alex 按照最优选择，都会让自己比 Lee 多 1，为了让 Lee 总分更多，Lee 会选 5，此时 Lee 得到的相对分数就是 4；
• • ③ 再考虑这里，Lee 可以选择 5 或者 4：
• • • Lee 选择 5 的时候，下一轮 Alex 会让自己多 1 分，因此选择 5 的时候，Lee 的相对分数是 5 - 1 = 4；
• • • Lee 选择 4 的时候，下一轮 Alex 会让自己多 2 分，因此选择 4 的时候，Lee 的相对分数是 4 - 2 = 2，
      Lee 为了得到最多的分数，会选择 5；
• • ④ 再考虑这里，Alex 可以选择左边 5 或者右边 5：
• • • Alex 选择左边 5 的时候，下一轮 Alex 会让自己多 4 分，因此选择左边 5 的时候，Alex 的相对分数是 5 - 4 = 1；
• • • Alex 选择右边 5 的时候，下一轮 Alex 会让自己多 4 分，因此选择右边 5 的时候，Alex 的相对分数是 5 - 4 = 1。
• • 所以 Alex 一定会赢，从上图中，我们发现两个 [3, 4]，出现重复子问题，因此，需要使用记忆化递归完成计算。
• Java 示例：

import java.util.Arrays;

public class Solution 

    public boolean stoneGame(int[] piles) 
        int len = piles.length;
        int[][] memo = new int[len][len];
        for (int i = 0; i < len; i++) 
            // 由于是相对分数，有可能是在负值里面选较大者，因此初始化的时候不能为 0
            Arrays.fill(memo[i], Integer.MIN_VALUE);
            memo[i][i] = piles[i];
        
        return stoneGame(piles, 0, len - 1, memo) > 0;
    


    /**
     * 计算子区间 [left, right] 里先手能够得到的分数
     *
     * @param piles
     * @param left
     * @param right
     * @return
     */
    private int stoneGame(int[] piles, int left, int right, int[][] memo) 
        if (left == right) 
            return piles[left];
        

        if (memo[left][right] != Integer.MIN_VALUE) 
            return memo[left][right];
        

        int chooseLeft = piles[left] - stoneGame(piles, left + 1, right, memo);
        int chooseRight = piles[right] - stoneGame(piles, left, right - 1, memo);
        int res = Math.max(chooseLeft, chooseRight);
        memo[left][right] = res;
        return res;
    

③ 动态规划

• 观察上面的记忆化数组 memo，是一个表格，并且状态转移方程比较容易看出：在拿左边石子堆和右边石子堆中做出对当前最好的选择。
• • 状态 dp[i][j] 定义：区间 piles[i…j] 内先手可以获得的相对分数；
• • 状态转移方程：dp[i][j] = max(nums[i] - dp[i + 1, j] , nums[j] - dp[i, j - 1]) 。
• 因此，在计算状态的时候，一定要保证左边一格和下边一格的值先计算出来。

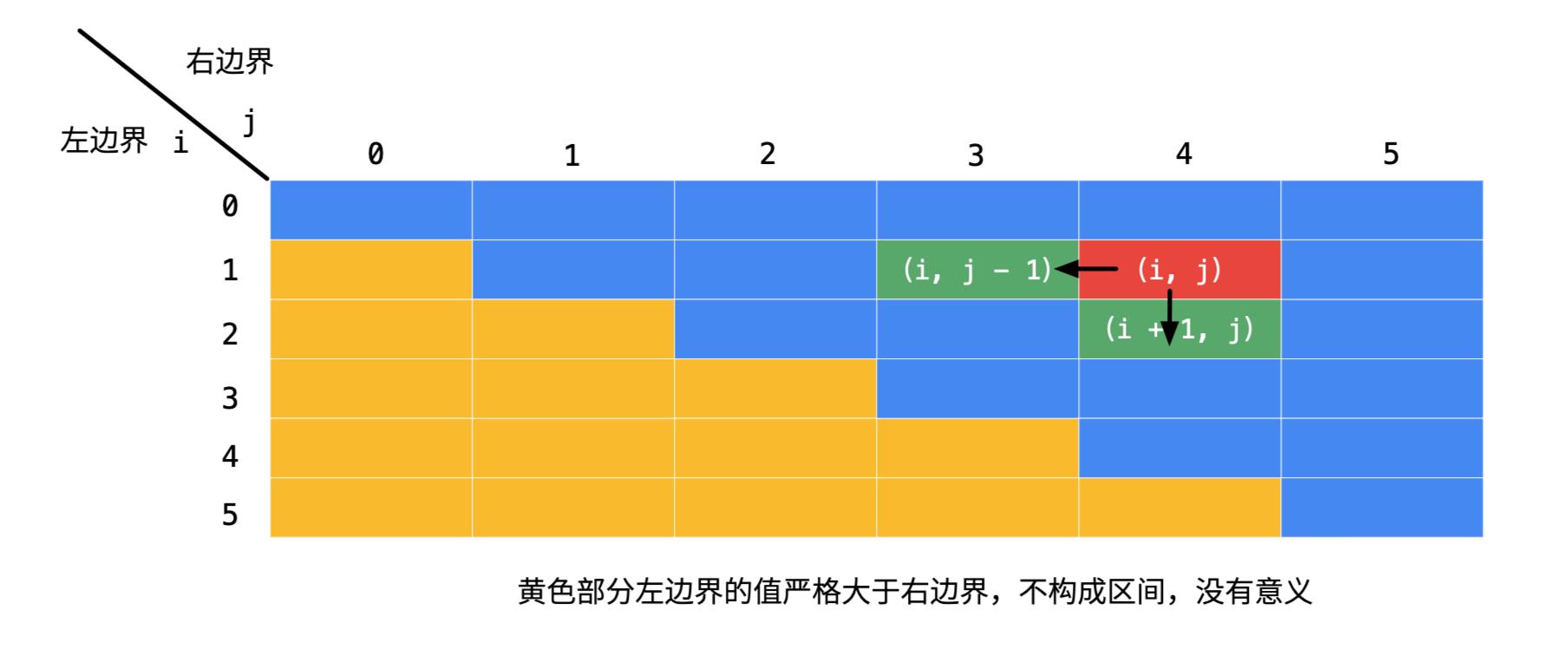
• 说明：
• • i 是区间左边界的下标，j 是区间右边界的下标；
• • 图中黄色部分不填，没有意义。
• 于是有以下两种填表顺序：
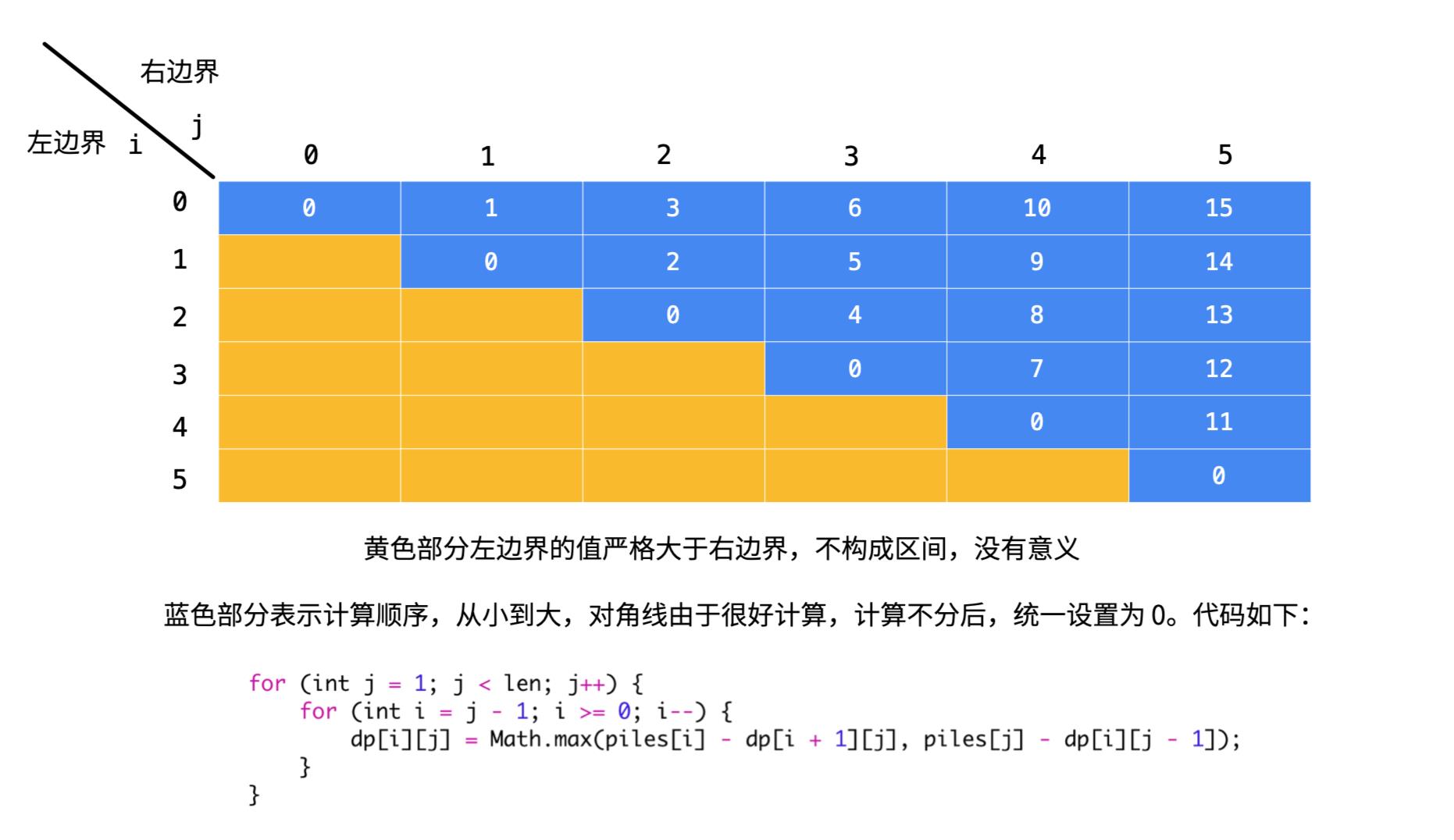
• • 填表顺序 1：

• • Java 示例：

public class Solution 

    // dp[i][j] 定义：区间 piles[i..j] 内先手可以获得的相对分数

    public boolean stoneGame(int[] piles) 
        int len = piles.length;
        int[][] dp = new int[len][len];
        for (int i = 0; i < len; i++) 
            dp[i][i] = piles[i];
        

        for (int j = 1; j < len; j++) 
            for (int i = j - 1; i >= 0; i--) 
                dp[i][j] = Math.max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
            
        
        return dp[0][len - 1] > 0;
    

• • 填表顺序 2：

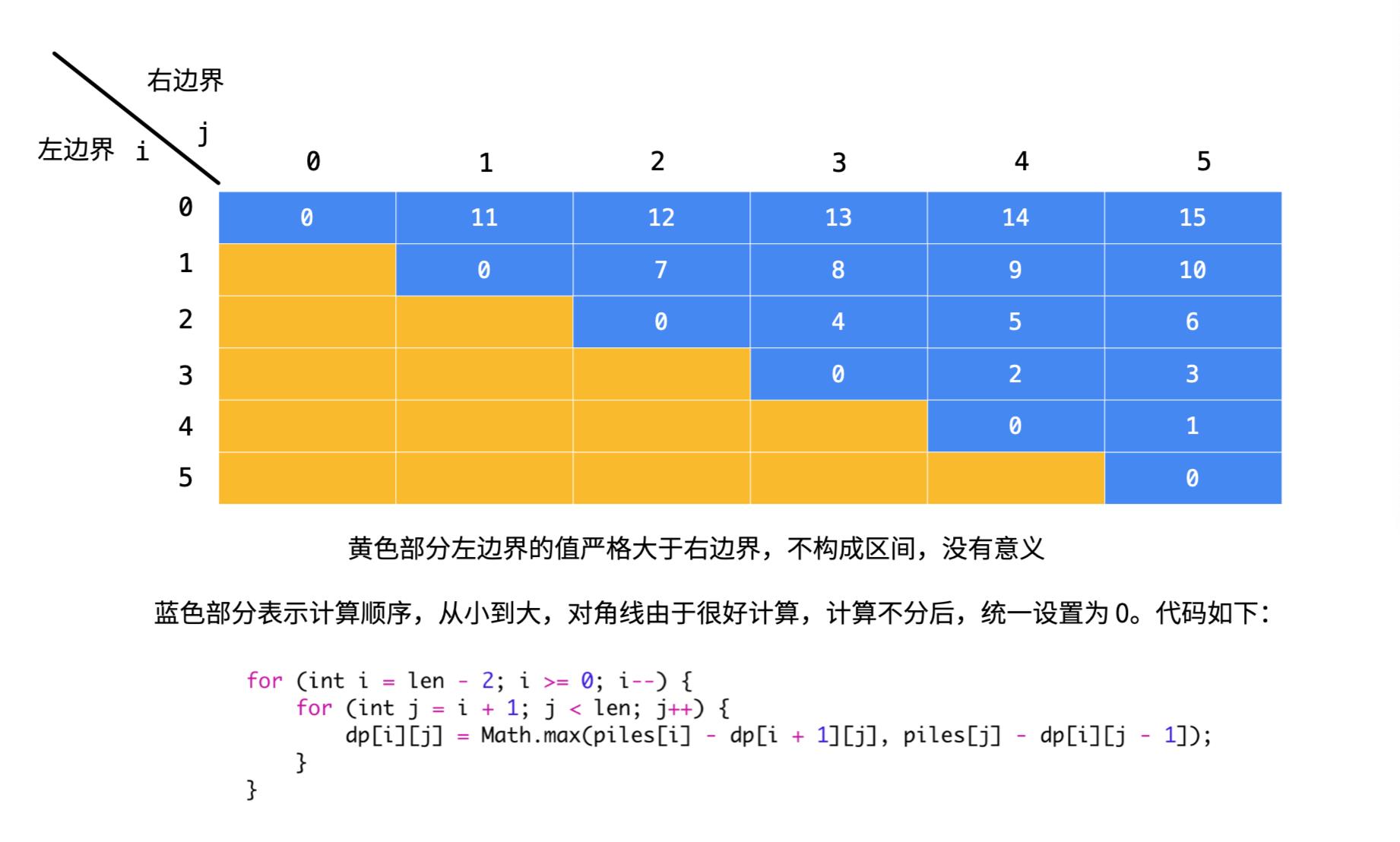
• • Java 示例：

public class Solution 

    // dp[i][j] 定义：区间 piles[i..j] 内先手可以获得的相对分数

    public boolean stoneGame(int[] piles) 
        int len = piles.length;
        int[][] dp = new int[len][len];
        for (int i = 0; i < len; i++) 
            dp[i][i] = piles[i];
        

        for (int i = len - 2; i >= 0; i--) 
            for (int j = i + 1; j < len; j++) 
                dp[i][j] = Math.max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
            
        
        return dp[0][len - 1] > 0;