多agv系统调度的MATLAB仿真

Posted 2022-01-14 fpga&matlab

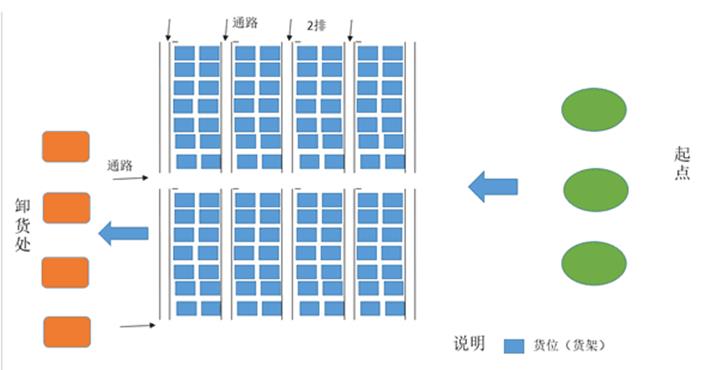
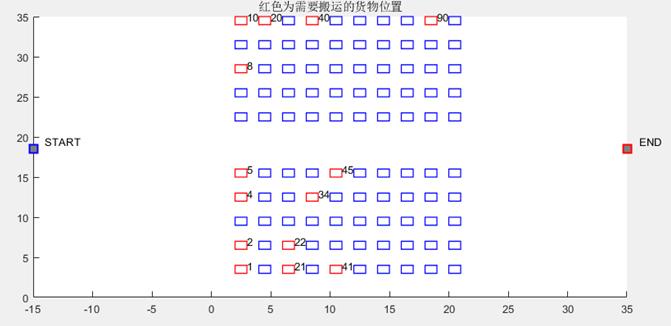
        从起点出发，到货物点领取货物最后到卸货点，以完成任务总时间最短为目标进行单目标优化，约束条件为，任务不冲突，路径不冲突，要能实现路径规避 ，4-6台agv一起工作。左右货架间隔可通过1个agv，上下货架间隔可通过两个agv，通道为双向行驶通道。一台agv只能带一个货物，优化目标为完成任务总的时间最短，agv的速度是匀速，转弯也不会减速，取货物时间为固定值。上面的图里面 货物看为正方形 跟agv一样的长度大小，agv试做是跟货物一样大小的正方形agv的速度是每秒1个车身。多台agv一起完成指定任务的时间最短，比如你可以设置三台agv一起取十个左右的货物到终点，使得这个时间最短。那就设置3台agv一起工作 取十个货物到终点 任务不冲突 路径不冲突 这样可以么，十个货物你可以在图片上面随便选。agv完成任务后从终点返回起点的时间和路径可以不计，或者可以把这个时间视作固定值 路径不会跟任务车辆冲突。

       场景的仿真效果如下所示：

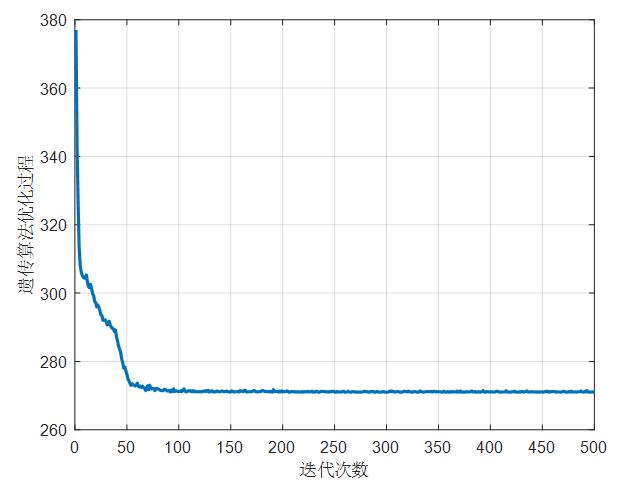
优化曲线

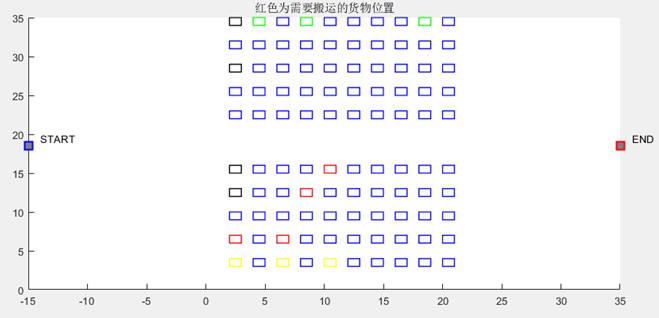
 优化后场景如下

 部分核心代码：

clc;
clear;
close all;
warning off;
addpath 'func\\'
addpath 'GA\\'

global N2;
global N1;
global W;
global W1;
global W2;
global W3;
global W4;
global V;
global Navg;
global X;
global Y;
global Starts;
global ends;
global Idx;
global Index;
global Xeach;
global Xpos;
global Ypos;
%产生地图
%上下每个区域的行数
N2 = 5;
%左右列数
N1 = 10;
%AGV大小
W  = 8;%这个地方不要改，保证坐标都是正数，方便内部计算处理
%左右货架间隔可通过1个agv
W1 = W/4;
%上下货架间隔可通过两个agv
W2 = W/4;
%上下两个区域的间隔
W3 = 2*W;
%货架大小
W4 = W;
%速度
V  = 1;

%AVG数量
Navg = 3;
[X,Y,Starts,ends,Idx,Xeach]=func_maps(N1,N2,W1,W2,W3,W4);
% Xeach(1:2:end)=Xeach(1:2:end)-W1/2;
% Xeach(2:2:end)=Xeach(2:2:end)+W4+W1/2;

%选择需要被搬运的货物编号
Index= [1,2,4,5,8,17,23,21,22,34,56,44,45,91];%设置最大值不超过2*N1*N2
Xpos = (X(Index));
Ypos = (Y(Index));

for i = 1:length(Xpos)
    idx = find(Xeach==Xpos(i));
    if mod(idx,2)==0;
       Xpos(i) = Xpos(i)+W4+W1/2;
    else
       Xpos(i) = Xpos(i)-W1/2;
    end
end

 
figure;
for i = 1:length(X)
    tmps = find(Index==i);
    
    if isempty(tmps)==1
       rectangle('Position', [[X(i),Y(i)] W4 W4], 'LineWidth', 1, 'EdgeColor', 'b', 'Clipping', 'off');
       hold on
    else
       rectangle('Position', [[X(i),Y(i)] W4 W4], 'LineWidth', 1, 'EdgeColor', 'r', 'Clipping', 'off');
       hold on
       text(X(i)+1,Y(i)+1,num2str(i));
    end
end
plot(Starts(1),Starts(2),'--gs',...
    'LineWidth',2,...
    'MarkerSize',10,...
    'MarkerEdgeColor','b',...
    'MarkerFaceColor',[0.5,0.5,0.5]);
hold on
text(Starts(1)+1,Starts(2)+1,'START');

plot(ends(1),ends(2),'--ys',...
    'LineWidth',2,...
    'MarkerSize',10,...
    'MarkerEdgeColor','r',...
    'MarkerFaceColor',[0.5,0.5,0.5]);

text(ends(1)+1,ends(2)+1,'END');
title('红色为需要搬运的货物位置');

 
MAXGEN = 50;
NIND   = 200;
Nums   = length(Index)+Navg+1; %优化变量数量，含义为N个货物的路线优化变量+每个AVG的搬运数量变量+冲突策略判断
Chrom  = crtbp(NIND,Nums*10);

%sh
Areas = [];
for i = 1:length(Index)
    Areas = [Areas,[1;length(Index)-i+1]];
end
for i = 1:Navg
    Areas = [Areas,[1;length(Index)-Navg+1]];%每个avg最多搬运N-AVG+1个，保证其他的至少可以搬运1个
end
for i = 1:1
    Areas = [Areas,[1;2]];%策略4选1
end

FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];

gen   = 0;

%计算对应的目标值
A = floor(length(Index)*rand(1,Navg))+1; 
S = sum(A); 
B = round(A*length(Index)/S);
if sum(B)>length(Index)
 [Vbb,Ibb]= max(B);
 B(Ibb) = B(Ibb)-(sum(B)-length(Index));
end
if sum(B)<length(Index)
 [Vbb,Ibb]= min(B);
 B(Ibb) = B(Ibb)+(length(Index)-sum(B));
end  
Xxx          = [1:length(Index),B,1];%初始值
fobj         = func_obj(Xxx);
E            = fobj;
Js           = E*ones(NIND,1);
Objv         = (Js+eps);
gen          = 0; 

%%
while gen < MAXGEN;   
      gen
      Pe0 = 0.9999;
      pe1 = 0.0001; 

      FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,Pe0);   
      Selch=mut( Selch,pe1);   
      phen1=bs2rv(Selch,FieldD);   
 
      for a=1:1:NIND  
          AA   = round(phen1(a,1:length(Index)));
          AA2  = [];
          Index_=Index;
          for i = 1:length(AA)
              AA2(i)=Index_(AA(i));
              Index_(AA(i))=[];
          end
          BB   = floor(phen1(a,1+length(Index):end-1))+1;
          S    = sum(BB); 
          BB2  = round(BB*length(Index)/S);
          if sum(BB2)>length(Index)
             [Vbb,Ibb]= max(BB2);
             BB2(Ibb) = BB2(Ibb)-(sum(BB2)-length(Index));
          end
          if sum(BB2)<length(Index)
             [Vbb,Ibb]= min(BB2);
             BB2(Ibb) = BB2(Ibb)+(length(Index)-sum(BB2));
          end   
          CC2  = round(phen1(a,end));
          
          X1   = [AA2,BB2,CC2];
 
          %计算对应的目标值
          [fobj,pathall] = func_obj(X1);
          E              = fobj;
          JJ(a,1)        = E;
          XXa          = X1;
          pathallXa    = pathall;
      end 
      
      Objvsel=(JJ);    
      [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen=gen+1; 
      %保存参数收敛过程和误差收敛过程以及函数值拟合结论
      Error(gen) = mean(JJ);
end 
clc;
figure;
plot(Error,'linewidth',2);
grid on
xlabel('迭代次数');
ylabel('遗传算法优化过程');

[V,I]=min(JJ);

XX_best      = XXI;
pathall_best = pathallXI;

 
idxx = XX_best(1:length(Index));
Nums = XX_best(1+length(Index):end-1);

Color1='r';
Color2='k';
Color3='g';
Color4='y';
Color5='m';
Color6='c';
 

%显示每个avg搬运的货物编号
S1=0;
E1=0;
for j = 1:length(Nums)
    if j == 1
       S1=E1+1;
       E1=S1+Nums(j)-1;
       selj=idxx(S1:E1); 
    else 
       S1=E1+1;
       E1=S1+Nums(j)-1;
       selj=idxx(S1:E1); 
    end
    selj
end

A-06-68