前缀和与差分

Posted 2022-01-14 时空旅客～

文章目录

• • 一维前缀和
  • 一维差分
  • 二维前缀和
  • 二维差分

一维前缀和

sum[i]=sum[i-1]+a[i];i>0
sum[i]=sum[0]=a[0] ;i=0
arr 1,3, 7, 5, 2
sum 1,4,11,16,18
sum[i]是0到i的区间和
如2到4的区间和,k-r
sum[r,k]=sum[k]-sum[r-1]; r>0,
r=0的时候， sum[k] r=0;

#define getsum(k,r) (k?sum[r]-sum[k-1]:sum[r])//获得k到r间的和,宏定义更加的方便
int get_sum(int k, int r,int *sum)

	if (k == 0)
	
		return sum[r];
	
	else
	
		return sum[r] - sum[k - 1];
	

int main()

	const int n = 5;
	int arr[5] =  1,3,7,5,2 ;
	int sum[5];//sum原来记录前缀和
	sum[0] = arr[0];//0单独记录
	int i = 1;
	for (i = 1; i < 5; i++)
	
		sum[i] = sum[i - 1] + arr[i];

	
	//获取前缀和
	//获得k到r的和
	printf("%d", getsum(2, 4));//得到2-4的区间和，使用宏的方法
	printf("%d->", get_sum(1, 3,sum));//
	
	return 0;

一维差分

再区间里面对区间值进行修改，如果使用普通的方法，操作一次的时间复杂度是O(N),如果要询问k次，时间复杂度就是O（n*k）
差分就是d[0]=a[0],d[1]=a[1]-a[0];,差分的前缀和就是原数组

//一开始
int d[6]=0;//比arr多开辟一个空间原来r+1
void add(int l,int r,int v)
 
	d[l] += v;//在l-r的区间上都加上一个val，就是d[l]+v,加了之后对后面的所有值都加了一个val，但是d[r+1]-v,把后面加起来的v都抵消掉，只保证r-l间改变
	d[r + 1] -=v;


int main()

memset(d,0,sizeof(d));
	int arr[5] =  1,3,7,5,2 ;
	add(2, 4, 5);//2-4都+5
	add(1, 3, 2);
	add(0, 2, -3);
	//将d取0进行操作 
	int i;
	for (i = 1; i < 5; i++)
	//对d进行做前缀和，就是要对arr改变的值
		d[i] += d[i - 1];
	
	for (i = 0; i < 5; i++)
	//将d加到arr上
		arr[i] += d[i];
		printf("%d ", arr[i]);
	
	memset(d, 0, sizeof(d));//用完了之后要将d还原为0，以免后续有重新再用d
	return 0;

二维前缀和

将矩阵进行操作，从（x1，y1）->(x2,y2)形成的矩阵，进行前缀和相加

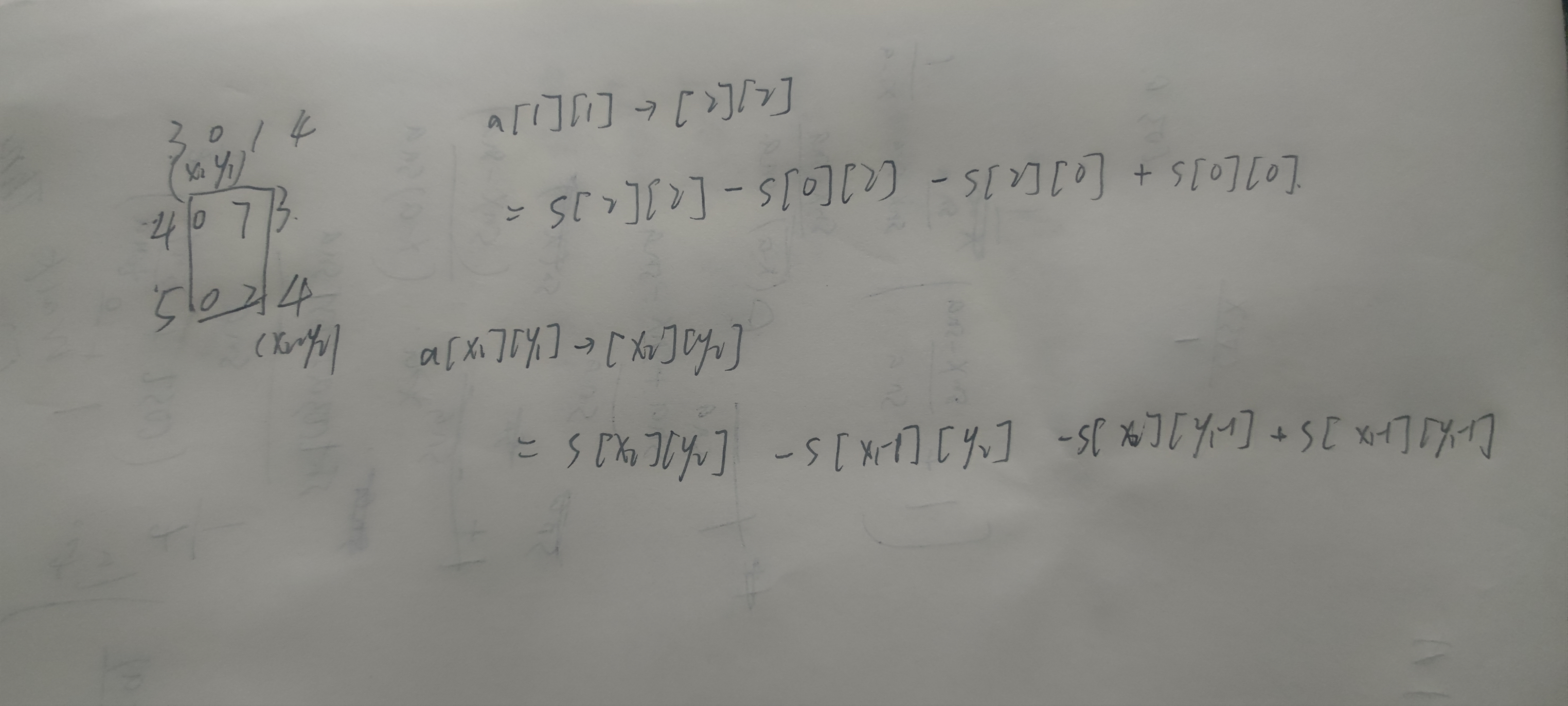
int main()


	int matrix[5][5] =  3,0,1,4,3,5,6,3,2,1,1,2,0,1,5,4,1,0,1,7,1,0,3,0,5 ;

	//计算二维数组的前缀和
	int sum[5][5];//sum[i][j]是从s[0][0]到s[i][j]形成的矩阵中进行前缀和相加
	int i, j;
	//计算前缀和，这里要用公式计算
	for (i = 0; i < 5; i++)
	
		for (j = 0; j < 5; j++)
		
			sum[i][j] = matrix[i][j];
			if (i - 1 > 0)
			
				sum[i][j] += sum[i - 1][j];
			
			if (j - 1 > 0)
			
				sum[i][j] += sum[i][j - 1];
			
			if (i - 1 > 0 && j - 1 > 0)
			
				sum[i][j] -= sum[i - 1][j - 1];
			

		
	
	//计算区间和
	//如[2,2]->[3,3];
	int row1 = 2, col1 = 2, row2 = 3, col2 = 3;
	int ans = sum[row2][col2];
	if (col1 - 1 > 0)
	
		ans -= sum[row2][col1 - 1];
	
	if (row1 - 1 > 0)
	
		ans -= sum[row1 - 1][col2];
	
	if (col1 - 1 > 0 && row1 - 1 > 0)
	
		ans += sum[row1 - 1][col1 - 1];
	
	printf("%d", ans);
	return 0;

二维差分

int d[5][5];
//二维前缀和
//二维差分
void add(int x1, int y1, int x2, int y2, int v)

	d[x1][y1] += v;
	d[x2 + 1][y1] -= v;
	d[x1][y2 + 1] -= v;
	d[x2 + 1][y2 + 1] += v;


void print(int** d, int x, int y)

	int i, j;
	for (i = 0; i < x; i++)
	
		for (j = 0; j < y; j++)
		
			printf("%d ", d[i][j]);
		
		printf("\\n");
	



int main()

	int matrix[3][4] =  1,5,6,8,9,6,7,3,5,3,2,4 ;

	memset(d, 0, sizeof(d));
	add( 0, 0, 2, 1, 3);
	add(1, 1, 2, 2, -1);
	int i, j;


	for (i = 0; i < 3; i++)
	
		for (j = 0; j < 4; j++)
		
			matrix[i][j] += d[i][j];
			printf("%d ", matrix[i][j]);
		
		printf("\\n");
	
	return 0;