交叉熵损失函数关于交叉熵损失函数的一些理解

Posted 2022-01-14 Rainbowman 0

目录

• 0. 前言
• 1.损失函数（Loss Function）
• • 1.1 损失项
  • 1.2 正则化项
• 2. 交叉熵损失函数
• • 2.1 softmax
  • 2.2 交叉熵

0. 前言

有段时间没写博客了，前段时间主要是在精读一些计算机视觉的论文（比如yolov1），以及学cs231n这门AI和计算机视觉领域的经典课程。我发现很多事情不能着急，质变需要量变的积累，违背事物发展的客观规律，往往适得其反。

今天在学习cs231n的时候看到了关于交叉熵损失函数的讲解，发现之前虽然经常用到这个损失函数，但却对里面的细节很模糊，学完之后更清晰了一些，所以做个总结笔记，方便以后快速回顾。学习就是不断重复的过程。

1.损失函数（Loss Function）

损失函数作用是：衡量真实值和模型预测值之间的差异。

为什么要有损失函数呢？

以分类任务为例，在神经网络中，模型前向传播求出每一类别的得分（score），然后将score带入损失函数中，求出Loss。再使用梯度下降法，反向传播，通过降低损失值（Loss）对模型的参数进行优化。

损失函数通常由损失项和正则化项组成。

1.1 损失项

损失项的目的就是之前说的，为了衡量真实值和模型预测值之间的差异。

1.2 正则化项

正则化项的目的是对高次项的特征进行惩罚，减轻过拟合的程度，进而可以提高模型的泛化能力。

常用的正则化有L1正则化和L2正则化。假如现在要训练一个线性模型，y = Wx + b，其中W就是我们要训练的参数（由w1,w2,…wn n个参数组成），b是偏置项。

则L1正则化就是

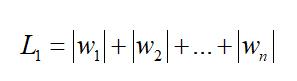
L2正则化为：

2. 交叉熵损失函数

交叉熵损失函数是多分类问题中很常用的损失函数，而交叉熵损失函数又离不开softmax函数。因为在多分类问题中，神经网络最后一层全连接层的原始输出只是每一类的得分（score）向量。比如以MINIST手写数字识别为例，我们构建的神经网络的最后一层肯定只有10个神经元（每个神经元输出0-9数字的得分）。

注意，这里10个神经元输出的只是得分，而非该图片属于该数字的概率。那要输出概率该怎么办呢？这就要用到sofrmax处理了。

2.1 softmax

softmax函数定义为：

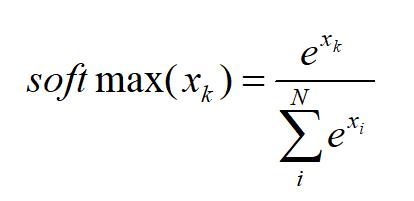
比如对于一个猫cat，狗dog，马horse的三分类问题，我们的神经网络最后一层给出每类得分为[10,9, 8]，那softmax应该这么求：

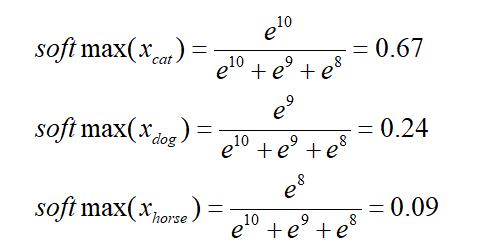
表示的含义是：模型推测该图片是猫的概率为67%，狗的概率为24%，马的概率为9%

用e^x求出的值恒为正，可以表示概率。

另外，从上面的例子也可以看出softmax可以把得分差距拉的更大：最后的全链接层得分输出为：[10,9,8]，相差其实不大。而经过softmax之后输出为：[0.67,0.24,0.09]，相对而言差距更大了。

2.2 交叉熵

终于说到交叉熵了，前面说了，交叉熵损失函数离不开softmax，应该先经过softmax求出每类的概率，再求交叉熵，可是为什么要这样呢？

这得从信息论中交叉熵的定义说起。交叉熵H(p,q)的定义为：

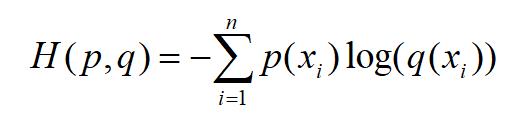
注意，这里的log是以e为底的！

其中p为真实概率分布，而q为预测的概率分布。既然是概率，那肯定得满足：每个值在0-1之间，且所有值的和为1。

说到这里，我们再拐回去看softmax函数的定义：

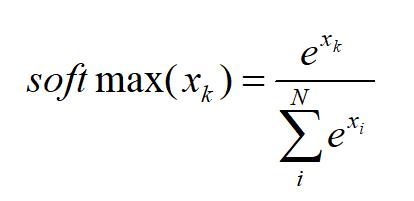
可以经过softmax层后的输出的每个值在0-1之间，且所有值的和为1。

这就是为什么在交叉熵损失函数中需要先进行softmax处理了，因为这是交叉熵本身的定义决定的（输入必须为概率）。

再来看交叉熵损失函数：

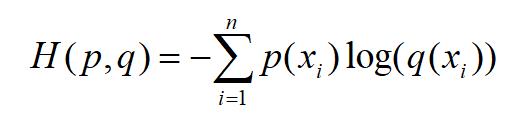
在机器学习中，真实概率分布p(xi）就是训练集的标签，预测的概率分布q(xi)就是我们模型预测的结果。再以刚刚的猫、狗、马三分类为例，我们提供一张猫的照片，则真实概率分布p(xi)的向量为[1, 0, 0]，而我们模型预测的概率分布q(xi)的向量为：[0.67, 0.24, 0.09]。

则对于该预测结果的交叉熵损失函数为：

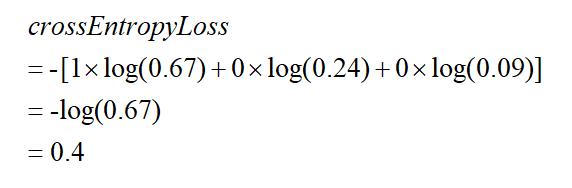
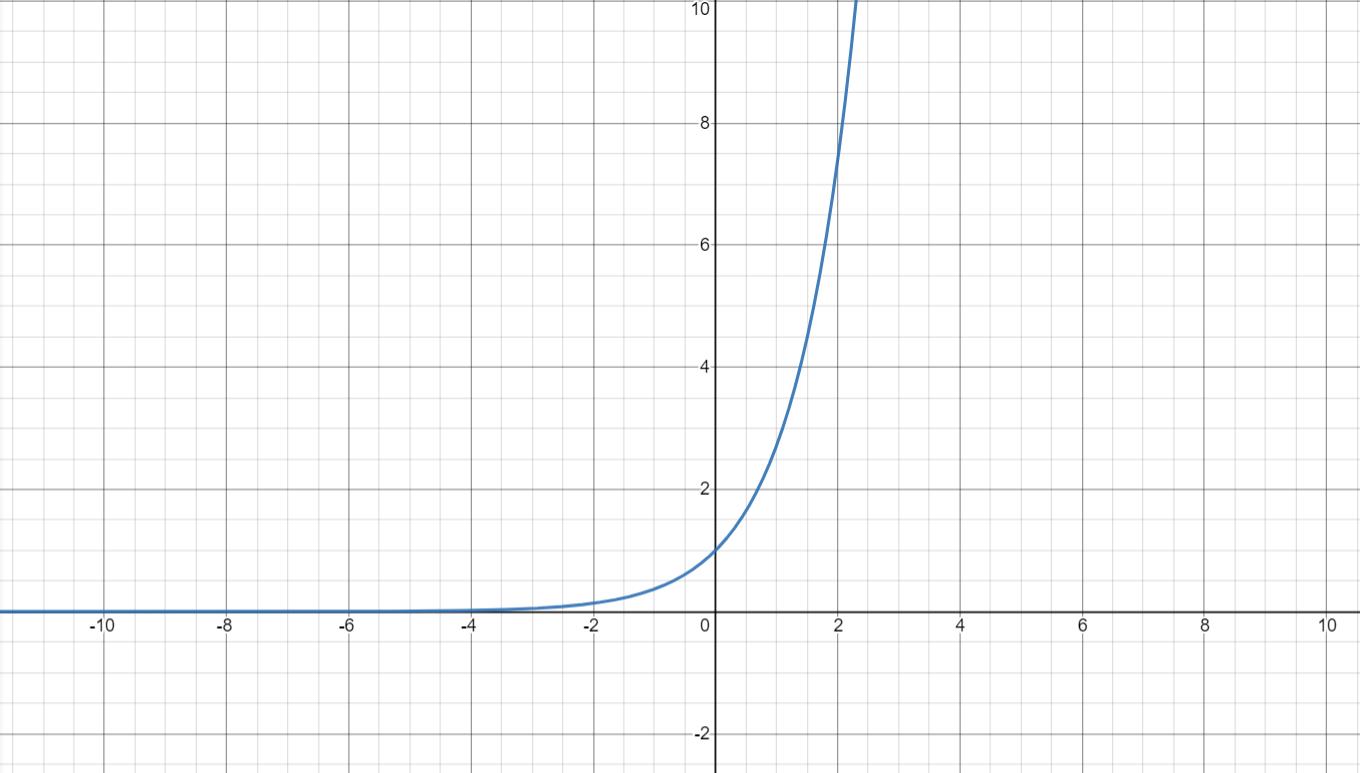
-log(x)函数

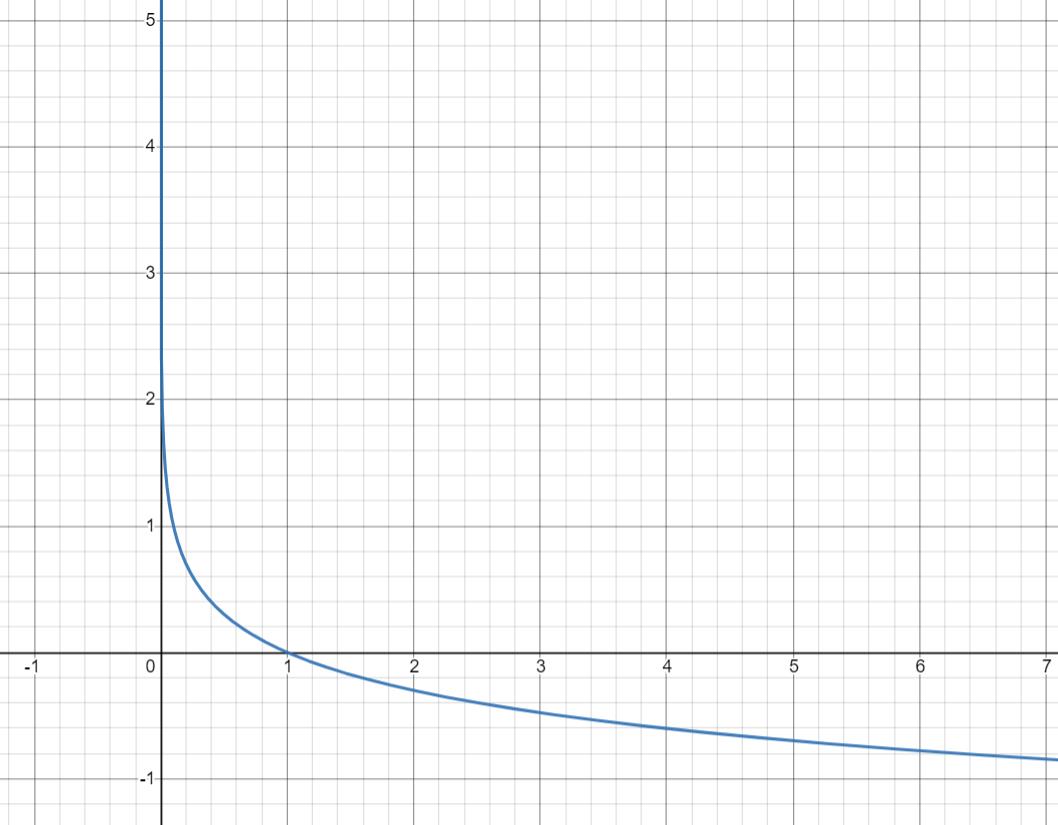
因为是-log(q(x))，而q(x)是概率，在0-1之间，所以我们只看0-1之间的函数样子。

不难看出：

（1）当预测结果正确时，该正确类别的概率越大（q(x)越接近1），交叉熵损失函数越小。

（2）当预测结果正确，但正确类别的概率不够大时（q(x)较小），交叉熵损失函数较大。

（3）当预测结果错误时，交叉熵损失函数也很大。

END：）

参考

交叉熵损失函数原理详解