运动学基于matlab GUI模拟小球自由落体含Matlab源码 1630期

Posted 2022-01-12 紫极神光

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源： 【运动学】基于matlab GUI模拟小球自由落体【含Matlab源码 1630期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、部分源代码

function bb()
% BB Bouncing Ball Physics
% BB is a graphical User Interface that creates a simple simulation of a ball bouncing
% off the ground. 
% 
% Ball Parameters are:
% 
% Height from the center of the ball to the ground is 10. This is constant and cannot
% change. Instead, change the other parameters since they're all relative.
% 
% Radius: Radius of the ball. It's best to put it between 1 and 9. Any value equal to
% or above 10 will present problems as 10 is the distance from the centre of the ball
% to the ground.
% 
% Gravity: Affect the ratio in which the ball gains speed in the negative Y direction.
% 
% Initial Yv: Initial velocity in the Y direction. Can be positive, negative, or anything.
% 
% Initial Xv: Initial velocity in the X direction. Can be positive, negative, or anything.
% 
% Vertical Speed Conservation (%): Affects how much energy (velocity) is retained in the
% Y direction after hitting the ground. A value of 0 to 100 is normal. A value of 0 means
% no energy is retained and the ball comes to a halt after hitting the ground. A value
% of 100 means all energy is retained and the ball will bounce indefinitely. A value of 
% over 100 will cause energy to increase after hitting the ground.
% 
% Horizontal Speed Conservation (%): Same as Vertical Speed Conservation but in the
% X direction.
% 
% Colour: Three element vector ([R G B]) in which the ball appears in. Each
% element should be between or equal 0 and 1.
% 
% 
% Plotting a path enables you to see the x-y diagram of the ball's movement and gives
% you the ability to pan the axes with the mouse.
%
% To launch the GUI, type bb in the command window with this file in the current
% directory. Alternatively, you can choose Debug -> Run from this editor window, or
% press F5.
%
%

figure('units','normalized','position',[.2 .2 .65 .65],'menubar','none','numbertitle','off','color','w','name','Bouncing Ball')
axes('position',[.25 .05 .65 .75])
ed1=uicontrol('style','edit','units','normalized','position',[.025 .895 .1 .05],'backgroundcolor','w','string','1','callback',@init);
uicontrol('style','text','units','normalized','position',[.025 .96 .1 .025],'backgroundcolor','w','string','Radius');
ed2=uicontrol('style','edit','units','normalized','position',[.025 .775 .1 .05],'backgroundcolor','w','string','9.81');
uicontrol('style','text','units','normalized','position',[.025 .84 .1 .025],'backgroundcolor','w','string','Gravity');
ed3=uicontrol('style','edit','units','normalized','position',[.025 .65 .1 .05],'backgroundcolor','w','string','0');
uicontrol('style','text','units','normalized','position',[.025 .72 .1 .025],'backgroundcolor','w','string','Initial Yv');
ed4=uicontrol('style','edit','units','normalized','position',[.025 .535 .1 .05],'backgroundcolor','w','string','500');
uicontrol('style','text','units','normalized','position',[.025 .6 .1 .025],'backgroundcolor','w','string','Initial Xv');
ed5=uicontrol('style','edit','units','normalized','position',[.025 .415 .1 .05],'backgroundcolor','w','string','70');
uicontrol('style','text','units','normalized','position',[.005 .48 .21 .025],'backgroundcolor','w','string',...
	'Vertical Speed Conservation (%)','horizontalalignment','left');
ed6=uicontrol('style','edit','units','normalized','position',[.025 .295 .1 .05],'backgroundcolor','w','string','50');
uicontrol('style','text','units','normalized','position',[.005 .36 .21 .025],'backgroundcolor','w','string',...
	'Horizontal Speed Conservation (%)','horizontalalignment','left');
ed7=uicontrol('style','edit','units','normalized','position',[.025 .175 .1 .05],'backgroundcolor','w','string','1 0 0','callback',@init);
uicontrol('style','text','units','normalized','position',[.025 .24 .1 .025],'backgroundcolor','w','string','Colour ([R G B])');
tb=uicontrol('style','togglebutton','string','Start','callback',@go,'units','normalized','position',[.025 .05 .1 .05],...
	'backgroundcolor','w');
chk=uicontrol('style','checkbox','string','Plot Path','units','normalized','position',[.025 .125 .1 .025],'backgroundcolor','w');

init;

	function [hb,h2,hx,h1,r,t]=init(varargin)
		r=str2double(get(ed1,'string'));
		t=linspace(0,2*pi,100);
		cla reset
		hold on
		cl=str2num(get(ed7,'string')); %#ok
		h1=fill((5)+r*cos(t),(10)+r*sin(t),cl);
		axis([0 10 -1 10+r+1])
		axis equal
		hx=axis;
		hL=line(1000.*[hx(1),hx(2)],[0 0]);
		set(hL,'color','k','linestyle','-','linewidth',3)
		hL=line(1000.*[hx(1),hx(2)],[10 10]);
		axis(hx)
		set(hL,'color','c','linestyle','--')
		set(h1,'linewidth',2)
		h2=plot(5,10,'k+');
		hb=[h1,h2];
	end

	function go(varargin)
		set(tb,'value',0)
		if strcmp(get(tb,'string'),'Start')			
			set(tb,'string','Stop')			
		else
			set(tb,'string','Start')
			return
		end
		dt=1;
		[hb,h2,hx,h1,r,t]=init;
		a=str2double(get(ed2,'string'))/2000;
		Yv=str2double(get(ed3,'string'))/2000;
		Xv=str2double(get(ed4,'string'))/2000;
		e=str2double(get(ed5,'string'))/100;
		f=str2double(get(ed6,'string'))/100;
		
		while strcmp(get(tb,'string'),'Stop')
			yc=get(h2,'ydata');
			if get(chk,'value')
				plot(get(h2,'xdata'),yc,'k.')
				pan on
			end
			Yv=Yv+a*dt;
			if yc-(Yv+a*dt)*dt<=r
				Yv=Yv+a*dt/(Yv+a*dt)*(yc-r);
				Yv=-Yv*e;
				set(h2,'ydata',r)
				set(h1,'ydata',r+(r)*sin(t))
				Xv=Xv*f;
			else
				for k=1:2
					set(hb(k),'ydata',get(hb(k),'ydata')-Yv*dt)
				end
			end

三、运行结果

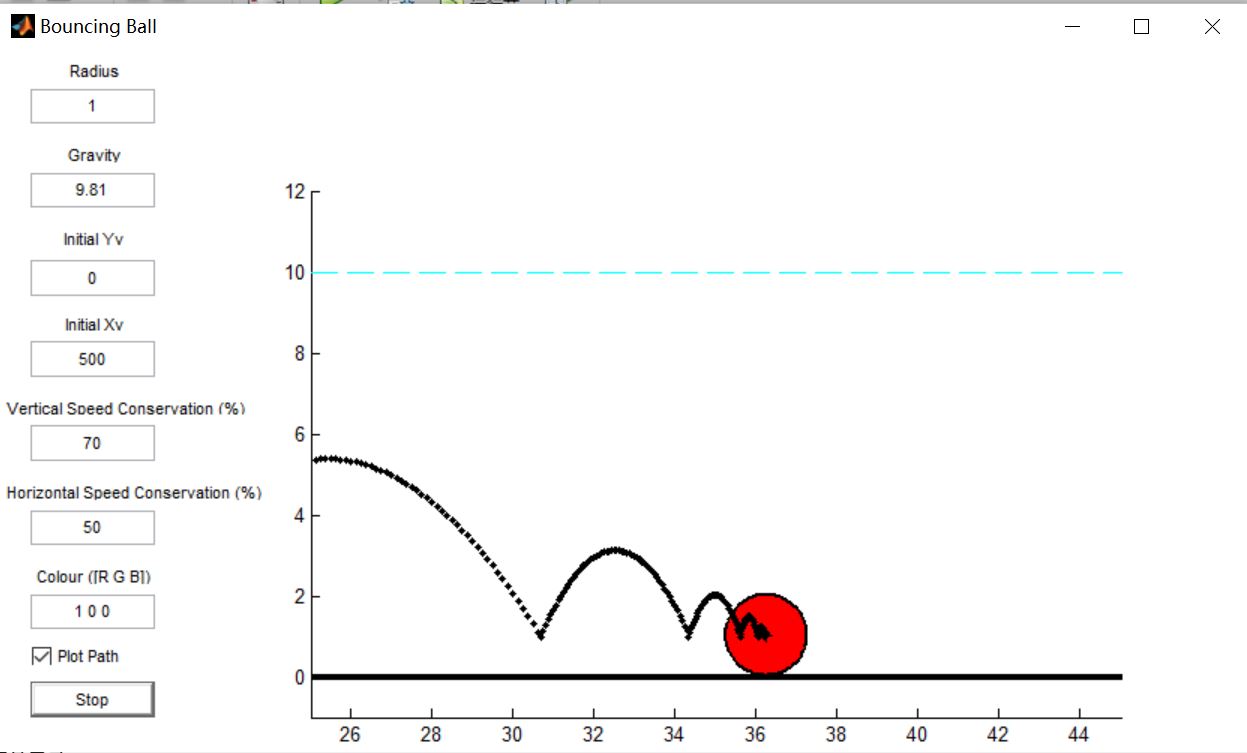
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 门云阁.MATLAB物理计算与可视化[M].清华大学出版社，2013.