数据分析与挖掘期末复习笔记（不挂科）

Posted 2022-01-12 ZSYL

【数据挖掘】期末复习笔记

• 1. 数据挖掘概论
• • 1.1 参考资料
  • 1.2 简介
  • 1.3 数据、信息、知识
  • 1.4 数据分析与数据挖掘
  • 1.5 主要任务
  • 1.6 数据库系统与数据仓库
  • 1.7 数据挖掘常用工具
  • 2. python数据分析与挖掘基础
  • 2.1 Matplotlib图表绘制基础
• 3. 认识数据
• • 3.1 属性及其类型
  • 3.2 数据的基本统计描述
  • 3.3 数据可视化
  • 3.4 数据对象的相似性度量
  • 3.5 小结
• 4. 数据预处理
• • 4.1 数据清洗
  • 4.2 数据集成
  • 4.3 相关分析
  • 4.4 相关系数
  • 4.5 数据规约
  • 4.6 数据转换和离散化
• 5. 分类
• • 5.1 朴素贝叶斯分类
  • 5.2 决策树
• 6. 聚类
• • 6.1 划分方法
• 7. 回归
• • 7.1 逻辑回归正则化
• 8. 关联分析
• • 8.1 频繁项集
  • 8.2 关联规则
  • 8.3 先验原理
  • 8.4 FP-tree挖掘频繁集
• 笔记
• • KDD
  • 聚类
  • 数据的属性类型
  • 四分位数极差(IQR)

1. 数据挖掘概论

1.1 参考资料

视频资料：魏伟一老师；MOOC官网，国防科大:丁兆云老师，北理：嵩天老师

1.2 简介

• 知识是人类对客观世界的观察和了解，是人类对客观世界是什么、为什么、应该怎么做的认知，知识推动人类的进步和发展。人类所作出的正确判断和决策，以及采取正确的行动都是基于智慧和知识。
• 数据是反映客观事物的数字、词语、声音和图像等，是可以进行计算加工的“原料”。数据是对客观事物的数量、属性、位置及其相互关系的抽象表示，适合于保存、传递和处理。

数据挖掘（Data Mining）是人工智能和数据库领域研究的热点问题，是指从大量有噪声的、不完全的、模糊和随机的数据中，提取出隐含在其中的、事先不知道但具有潜在利用价值的信息的过程。

这个定义包括几层含义：数据必须是真实的、大量的并且含有噪声的；发现的是用户感兴趣的可以接受、理解和运用的知识；仅支持特定的问题，并不要求放之四海而皆准的知识。

与数据挖掘的含义类似的还有一些术语如从数据中心挖掘知识、知识提取、数据/模式分析等。

数据挖掘–从大量数据中寻找其规律的技术，是统计学、数据库技术和人工智能技术的综合。

1.3 数据、信息、知识

• “8,000”和“10,000”是数据
• “8,000米是飞机飞行最大高度”与“10,000米的高山”是信息
• “飞机无法飞越这座高山”是知识
• “飞机必须飞得比山高”是智慧

面对大量的数据，迫使人们不断寻找新的工具，对规律进行探索，为决策提供有价值的信息。数据挖掘有助于发现趋势，揭示已知的事实，预测未知的结果。

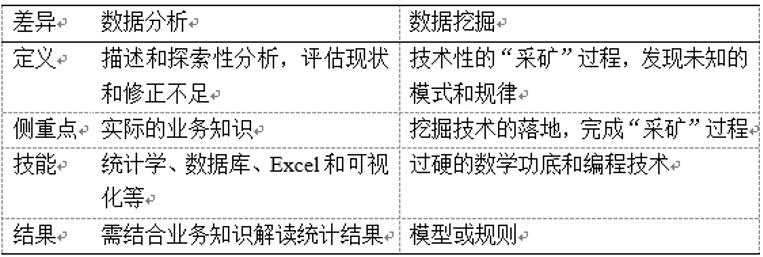
1.4 数据分析与数据挖掘

1.5 主要任务

数据挖掘是通过分析每个数据，从大量数据中寻找其规律的技术

数据挖掘：知识挖掘的核心

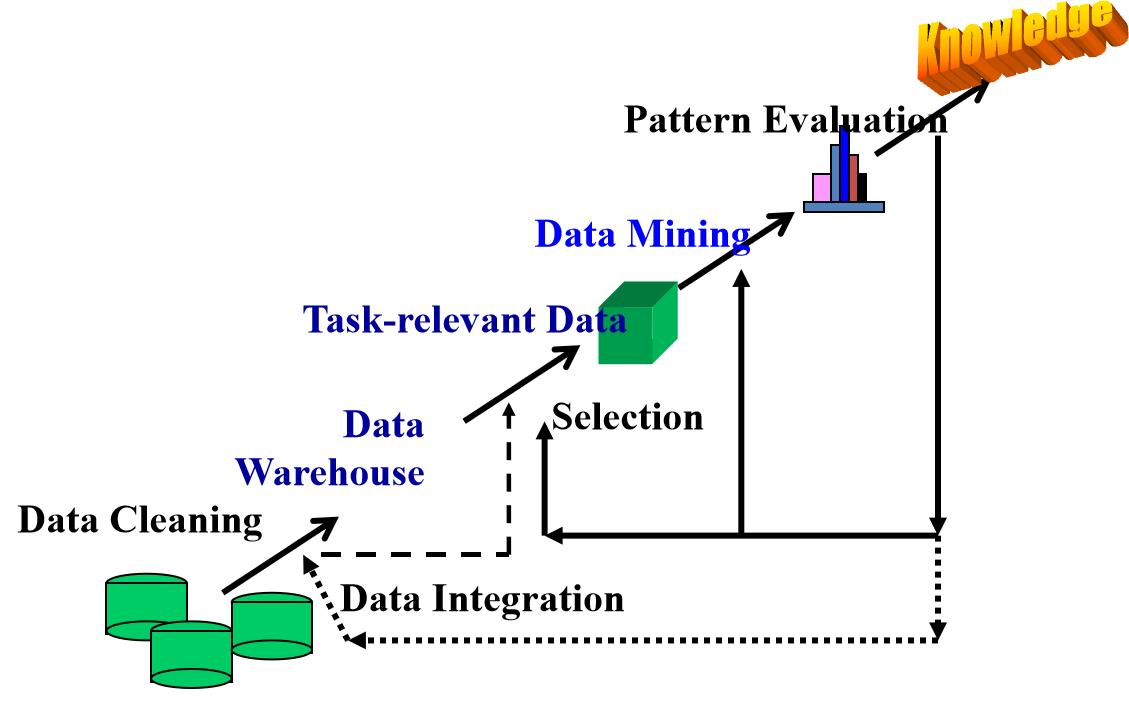
1.6 数据库系统与数据仓库

• 数据库管理系统（Database Management System，DBMS）是一种操纵和管理数据库的大型软件，主要关注数据库的创建、维护和使用。
• 数据仓库（Datawarehouse）是面向主题的、集成的与时间相关且不可修改的数据集合。
• 数据库主要用于事务处理，数据仓库主要用于数据分析，用途上的差异决定了两种架构的特点不同。

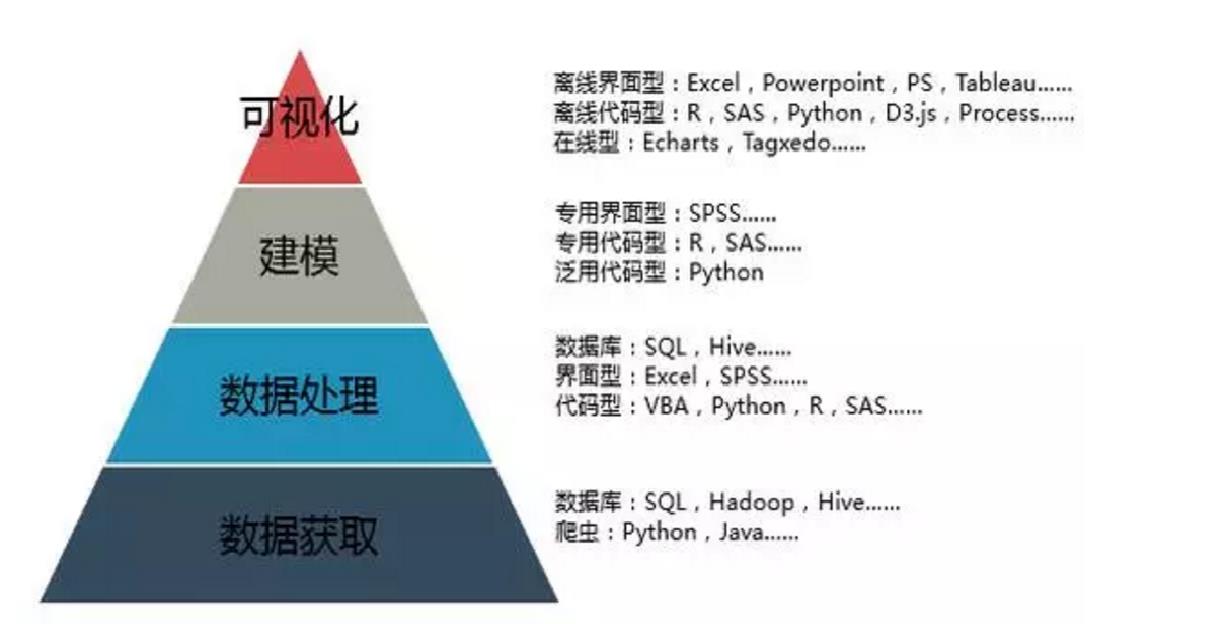
1.7 数据挖掘常用工具

1 商用工具

SAS Enterprise Miner
SPSS Clementine
Intelligent Miner
QUEST

2 开源工具

R
Weka
Mahout
RapidMiner
Python
Spark MLlib

Python进行数据挖掘的优势

2. python数据分析与挖掘基础

2.1 Matplotlib图表绘制基础

文本注解

绘图时有时需要在图表中加文本注解，Python通过text函数在指定的位置（x,y）加入文本注解，也可以利用annotate()完成指向型注释。

3. 认识数据

3.1 属性及其类型

• 属性：（Attribute）是一个数据字段，表示数据对象的一个特征。在文献中，属性、维（Dimension）、特征（Feature）和变量（Variable）表示相同的含义，可以在不同场合互换使用。
• 属性类型：属性的取值范围决定了属性的类型。

标称属性

标称属性（Nominal Attribute）的值是一些符号或事物的名称。每个值代表某种类别、编码或状态，因此标称属性又可称为是分类的（Categorical）。

标称属性的值是枚举的，可以用数字表示这些符号或名称。常见的标称属性如姓名、籍贯、邮政编码或婚姻状态等。标称属性的值不仅仅是不同的名字，它提供了足够的信息用于区分对象。

二元属性

二元属性（Binary Attribute）是标称属性的特例，也是一种布尔属性，对应0和1两个状态，二元属性分为对称的和非对称的。

序数属性

序数属性（Ordinal Attribute）的可能值之间存在有意义的序或秩评定，但是相继值之间的差是未知的。

数值属性

数值属性（Numeric Attribute）是可以度量的量，用整数或实数值表示，常见的数值属性如年龄。数值属性可以是区间标度的或比率标度的。

3.2 数据的基本统计描述

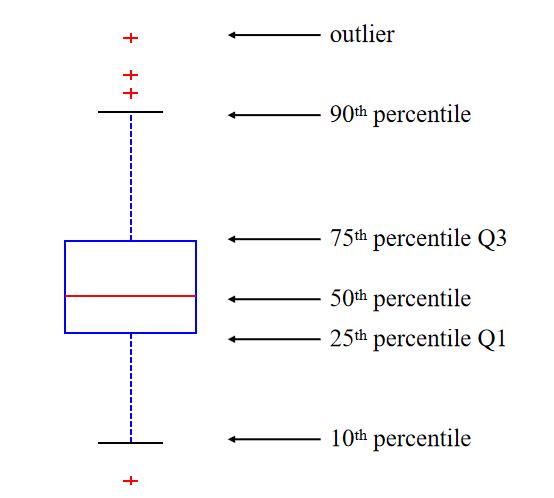
数据散布度量包括极差、分位数、四分位数、百分位数和四分位数极差。方差和标准差也可以描述数据分布的散布。

四分位数中Q3到Q1之间的距离的差的一半又称为分半四分位差，记为（Q3-Q1）/2。

• 盒图的边界分别为第一四分位数和第三四分位数
• 在箱体上中位数即第二四分数处画垂线
• 虚线被称为触须线，触须线的端点为最小值和最大值
• 利用四分位数间距IQR = Q3-Q1，找到界限，超出即为异常值。
• IQR左 = Q1 - 1.5×IQR
• IQR右 = Q3 + 1.5×IQR

3.3 数据可视化

降维方法将高维数据投影到低维空间，尽量保留高维空间中原有的特性和聚类关系。常见的降维方法有主成分分析、多维度分析（Multi-Dimensional Scaling, MDS）和自组织图（Self-Organization Map, SOM） 等。

常用的数据降维方法如下：

3.4 数据对象的相似性度量

• 现实中，我们需要处理的数据具有着不同的形式和特征。而对数据相似性的度量又是数据挖掘分析中非常重要的环节。
• 数据矩阵与相异性矩阵

标称属性的相似性度量

二元属性的相似性度量

• 对于对称的二元属性，两个状态是同等重要的。如果对象i和j都用对称的二元属性刻画，则i和j的相异性定义为：
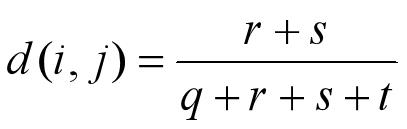
  数值属性的相似性度量

曼哈顿距离

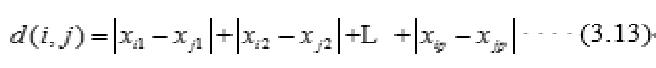
切比雪夫距离

闵可夫斯基距离

汉明距离（Hamming Distance）

两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要做的最小替换次数。

余弦相似性

针对文档数据的相似度测量一般使用余弦相似性。在处理文档的时候，一般采用文档所拥有的关键词来刻画一个文档的特征。

3.5 小结

• 数据集由数据对象组成。数据对象代表实体，用属性描述。
• 数据属性有标称、二元的、序数的或数值的。
• 数据的基本统计描述为数据预处理提供了分析的基础。
• 数据概括的基本统计量包括度量数据中心趋势的均值、加权均值、中位数和众数，以及度量数据散布的极差、分位数、四分位数、四分位数极差、方差和标准差等。
• 数据可视化技术主要有基于像素的、基于图标或层次的方法。
• 数据对象的相似性度量用于诸如聚类、离群点分析等应用中。相似度度量基于相似性矩阵，对每种属性类型或其组合进行相似度计算。

4. 数据预处理

4.1 数据清洗

• 忽略元组：当类标号缺少时通常这么做（监督式机器学习中训练集缺乏类标签）。当每个属性缺少值比例比较大时，它的效果非常差

• 手动填写遗漏值：工作量大

• 自动填写

  • 使用属性的平均值填充空缺值
  • 最有可能的值：基于诸如贝叶斯公式或决策树推理

• 盒状图检测离群数据：删除离群点
  
  数据库中某属性缺失值比较多时，数据清理采用的方法 平均值填充

4.2 数据集成

将来自多个数据源的数据组合成一个连贯的数据源

• 通过相关性分析和协方差分析可以检测到冗余的属性

4.3 相关分析

• $X^2$值越大，越有可能变量是相关的

• 相关性并不意味着因果关系

4.4 相关系数

相关系数（也称为皮尔逊相关系数）

其中n是元组的数目，而p和q是各自属性的具体值， σp和σq是各自的标准偏差

当r>0时，表示两变量正相关，r<0时，两变量为负相关。
当|r|=1时，表示两变量为完全线性相关，即为函数关系。
当r=0时，表示两变量间无线性相关关系。
当0<|r|<1时，表示两变量存在一定程度的线性相关。且|r|越接近1，  两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱。
一般可按三级划分：|r|<0.4为低度线性相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关。

4.5 数据规约

• 为什么数据规约（data reductio）？

  • 由于数据仓库可以存储TB的数据，因此在一个完整的数据集上运行时，复杂的数据分析可能需要一个很长的时间

• 降维

• 降数据

• 数据压缩

类似神经网络的机器学习方法，主要需要学习各个特征的权值参数 。特征越多，需要学习的参数越多，则模型越复杂

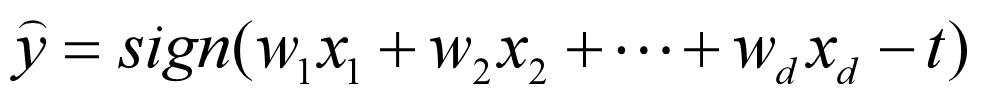
• 机器学习训练集原则：模型越复杂，需要更多的训练集来学习模型参数，否则模型将欠拟合。

• 因此，如果数据集维度很高，而训练集数目很少，在使用复杂的机器学习模型的时候，首选先降维。

总结：需要降维的场景

• 数据稀疏，维度高
• 高维数据采用基于规则的分类方法
• 采用复杂模型，但是训练集数目较少
• 需要可视化

PCA主成分分析法

• 数据中很多属性之间可能存在这样或那样的相关性
• 能不能找到一个方法，将多个相关性的属性组合仅仅形成一个属性？
• 主成分分析就是设法将原来众多具有一定相关性的属性（比如 p个属性），重新组合成一组相互无关的综合属性来代替原来属性。通常数学上的处理就是将原来 p个属性作线性组合，作为新的综合属性

• 线性变换等价于坐标旋转
• 主成分分析几何意义：寻找主轴

为什么数据规约（data reductio）？

• 由于数据仓库可以存储TB的数据，因此在一个完整的数据集上运行时，复杂的数据分析可能需要一个很长的时间.
• 降维
  • PCA主成分法
• 降数据
  • 抽样法
• 数据压缩

4.6 数据转换和离散化

函数映射指给定的属性值更换了一个新的表示方法，每个旧值与新的值可以被识别

• 规范化：按比例缩放到一个具体区间

  • 最小 - 最大规范化
    

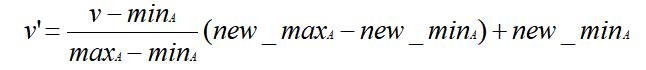
  • Z-得分正常化
    

  • 小数定标规范化：移动属性A的小数点位置(移动位数依赖于属性A的最大值)
    

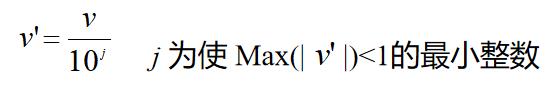
• 离散化

非监督离散化法

• 等宽法
  • 根据属性的值域来划分，使每个区间的宽度相等
• 等频法
  • 根据取值出现的频数来划分，将属性的值域划分成个小区间，并且要求落在每个区间的样本数目相等
• 聚类
  • 利用聚类将数据划分到不同的离散类别

5. 分类

分类与预测

• 分类是预测分类（离散、无序）标号
• 预测建立连续值函数模型

分类与聚类

• 分类是有监督学习，提供了训练元组的类标号
• 聚类是无监督学习，不依赖有类标号的训练实例

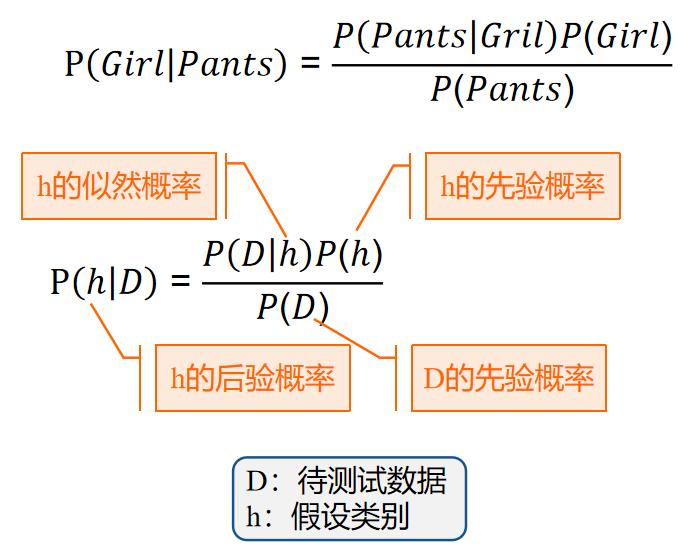
5.1 朴素贝叶斯分类

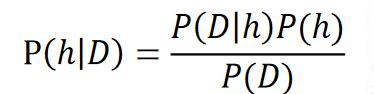
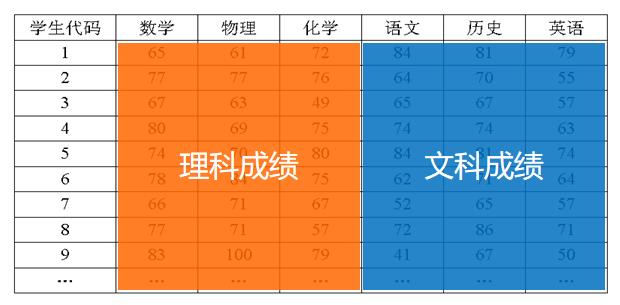
一所学校里面有 60% 的男生(boy)，40% 的女生(girl) 。男生总是穿长裤(pants)，女生则一半穿长裤一半穿裙子。随机选取一个穿长裤的学生，他（她）是女生的概率是多大？

形式化

已知P(Boy)=60%, P(Girl)=40%, P(Pants|Girl)=50%, P(Pants|Boy)=100%

求：P(Girl|Pants)

解答

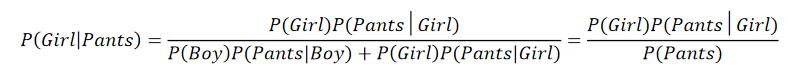
直观理解

算出学校里面有多少穿长裤的，然后在这些人里面再算出有多少女生。

5.2 决策树

决策分支画成图形很像一棵树的枝干，故称决策树

有许多决策树算法：

• Hunt算法：Hunt算法采用贪心策略构建决策树
• 信息增益——Information gain （ID3）
• 增益比率——Gain ration（ID3，C4.5）
• 基尼指数——Gini index (SLIQ，SPRINT)

6. 聚类

物以类聚、人以群分

6.1 划分方法

划分方法：将有n 个对象的数据集D划分成k个簇，并且k≤n，满足如下的要求：

• 每个簇至少包含一个对象
• 每个对象属于且仅属于一个簇

基本思想

• 首先创建一个初始k划分( k为要构造的划分数)
• 然后不断迭代地计算各个簇的聚类中心并依新的聚类中心调整聚类情况，直至收敛

目标

• 同一个簇中的对象之间尽可能“接近”或相关
• 不同簇中的对象之间尽可能“远离”或不同

7. 回归

回归分析是研究一个或多个自变量与一个因变量之间是否存在某种线性关系或非线性关系的一种统计学方法。

7.1 逻辑回归正则化

重写误差函数lambda是W的权重牺牲正确率来提高推广能力:

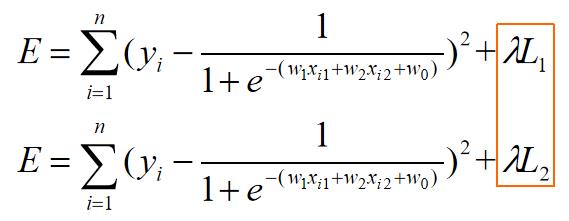
惩罚项：若学习到大权值使得误差小，但是再加上正则化式子以后使得上面E值变大。

因此，最小化E值使得求解的权值尽可能相对较小。

一个有趣的结论

logistic回归对噪声敏感。

8. 关联分析

关联分析用于发现隐藏在大型数据集中的令人感兴趣的联系，所发现的模式通常用关联规则或频繁项集的形式表示。

关联规则反映一个事物与其它事物之间的相互依存性和关联性。如果两个或者多个事物之间存在一定的关联关系，那么，其中一个事物发生就能够预测与它相关联的其它事物的发生。

8.1 频繁项集

项集（Itemset）

• 包含0个或多个项的集合
  • 例子： Milk, Bread, Diaper
• k-项集
  • 如果一个项集包含k个项

支持度计数（Support count）

• 包含特定项集的事务个数
• 例如：$\sigma$(Milk, Bread,Diaper) = 2

支持度（Support）

• 包含项集的事务数与总事务数的比值
• 例如：s(Milk, Bread, Diaper) = 2/5

频繁项集（Frequent Itemset）

• 满足最小支持度阈值（minsup）的所有项集

8.2 关联规则

关联规则是形如 X->Y 的蕴含表达式, 其中 X 和 Y 是不相交的项集

例子：

Milk, Diaper->Beer

关联规则的强度

• 支持度 Support (s)

  • 确定项集的频繁程度

• 置信度 Confidence（c）

  • 确定Y在包含X的事
  • 事务中出现的频繁程度

关联规则挖掘问题：

• 给定事务的集合 T, 关联规则发现是指找出支持度大于等于 minsup 并且置信度大于等于minconf的所有规则, minsup和minconf是对应的支持度和置信度阈值。

8.3 先验原理

• 如果一个项集是频繁的，则它的所有子集一定也是频繁的
• 相反，如果一个项集是非频繁的，则它的所有超集也一定是非频繁的

8.4 FP-tree挖掘频繁集

基本思想 (分治)

• 用FP-tree递归增长频繁集

方法

• 对每个项，生成它的条件模式基, 然后生成它的条件 FP-tree
• 对每个新生成的条件FP-tree，重复这个步骤
• 直到结果FP-tree为空， 或只含唯一的一个路径 (此路径的每个子路径对应的项集都是频繁集)

笔记

KDD

• KDD全称Knowledge Discovery in Database：数据挖掘与知识发现

聚类

• 聚类（Clustering）是把数据对象划分成子集的过程，就是将数据分组成为多个类（Cluster）。在同一个类内对象之间具有较高的相似度，不同类之间的对象之间的差异较大。

数据的属性类型

数据的属性类型有：
　　1、标称属性。
　　标称属性的值是一些符号或实物的名称，每个值代表某种类别、编码或状态，所以标称属性又被看做是分类型的属性（categorical）。这些值不必具有有意义的序，并且不是定量的。
　　2、二元属性。
　　二元属性是一种标称属性，只有两个类别或状态：0或1，其中0常表示不出现，1表示出现。如果将0和1对应于false和true，二元属性则为布尔属性。
　　3、序数属性。
　　序数属性可能的取值之间具有有意义的序或秩评定，但相继值之间的差是未知的。例如，学生的成绩属性可以分为优、良、中、差四个等级；某快餐店的饮料杯具有大、中、小三个可能值。然而，具体“大”比“中”大多少是未知的。
　　4、数值属性。
　　数值属性是可度量的量，用整数或实数值表示，有区间标度和比率标度两种类型。区间标度属性：区间标度属性用相等的单位尺度度量。区间属性的值有序。所以，除了秩评定之外，这种属性允许比较和定量评估值之间的差；比率标度属性：比率标度属性的度量是比率的，可以用比率来描述两个值，即一个值是另一个值的倍数，也可以计算值之间的差。
　　5、离散属性与连续属性。
　　离散属性具有有限或无限可数个值。如学生成绩属性，优、良、中、差；二元属性取1和0以及年龄属性取0到110。如一个属性可能取值的值集合是无限的，但可以建立一个与自然数的一一对应，则其也是离散属性。如果一个属性不是离散的，则它是连续的。

四分位数极差(IQR)

四分位差（quartile deviation），它是上四分位数（Q3，即位于75%）与下四分位数（Q1，即位于25%）的差。

计算公式为：Q = Q3-Q1

四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中；其数值越大，说明中间的数据越分散。四分位差不受极值的影响。此外，由于中位数处于数据的中间位置，因此，四分位差的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位差主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位差，但不适合分类数据。

四分位数是将一组数据由小到大（或由大到小）排序后，用3个点将全部数据分为4等份，与这3个点位置上相对应的数值称为四分位数，分别记为Q1（第一四分位数），说明数据中有25%的数据小于或等于Q1，Q2（第二四分位数，即中位数）说明数据中有50%的数据小于或等于Q2、Q3（第三四分位数）说明数据中有75%的数据小于或等于Q3。其中，Q3到Q1之间的距离的差的一半又称为分半四分位差，记为（Q3-Q1）/2。