推荐系统笔记：使用分类模型进行协同过滤

Posted 2022-01-12 UQI-LIUWJ

1 适用问题限制

        许多其他分类方法可以扩展到协同过滤的情况。这些方法的主要挑战是数据的不完整性质。在某些分类器的情况下，更难以调整模型来处理缺失属性值的情况。一个例外是一元数据的情况，其中缺失值通常估计为 0，并且指定的条目设置为 1。

        因此，底层矩阵类似于高维的稀疏二进制数据。在这种情况下，可以将数据视为一个完整的数据集，并且可以使用为稀疏和高维数据设计的任何分类器。

        幸运的是，许多形式的数据，包括客户交易数据、Web 点击数据或其他活动数据，都可以表述为一元矩阵。值得注意的是，文本数据也是稀疏高维的；因此，的许多分类算法都可以直接适应这些数据集。

        对于评级矩阵不是一元的情况，不再可能在不引起显着偏差的情况下用 0 填充矩阵的缺失条目。

        我们可以使用降维方法来创建数据的低维完整表示。 在这种情况下，通过将低维表示作为训练数据的特征变量，可以有效地使用任何已知的分类方法。 任何需要补全的列都被视为类变量。

        这种方法的主要问题是在分类过程中失去了可解释性。  很难对预测提供合理的解释 ...        

2 解决方法

        为了在原始特征空间中工作，可以将分类/回归方法作为元算法与迭代方法结合使用。  换句话说，现成的分类算法被用作黑盒来预测其中一个项目的评分与其他项目的评分。

        如何克服训练数据不全的问题？ 诀窍是通过连续迭代更新训练列的缺失值。 这种连续的更新是通过使用我们的黑盒实现的，这是一种现成的分类（或回归建模）算法  

        考虑任意分类/回归建模算法 A，该算法旨在处理数据完全的矩阵。

        第一步是使用行平均值、列平均值或任何简单的协同过滤算法初始化矩阵中缺失的条目。

，迭代循环由两小步组成：

• 迭代循环第一小步：使用算法A估计每一列的缺失条目，将其设置为目标变量，将剩余的列设置为特征变量。 对于其他特征列，第一次迭代使用行平均值、列平均值或任何简单的协同过滤算法补全矩阵中缺失的条目。之后轮次的迭代使用上一轮更新的矩阵。 目标列中观察到的评分用于训练，并预测缺失的评分。（此时只记录，不更新）
• 迭代循环第二小步：将第一步求得的每一列的预测结果进行更新，得到本轮迭代结束后的矩阵

        这两个步骤迭代执行直到收敛。

        该方法可能对初始化的质量和算法 A 很敏感。不过，该方法的优点是它是一种简单的方法，可以很容易地使用任何现成的分类或回归模型来实现。 数值评级也可以用线性回归模型处理。

3 举例：使用最简单的神经网络进行协同过滤

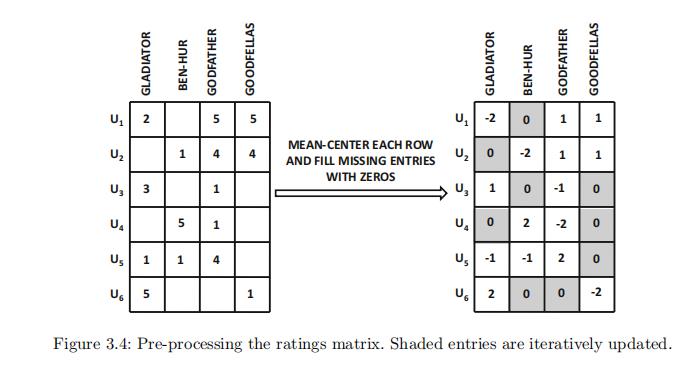
        考虑一个包含四个项目的评分矩阵，如图 3.4 的左侧所示。

        这里做了一个小trick，就是对每一行的观测值进行均值居中，以消除用户偏见。（每一行的观测值减去这一行的观测值均值。）。然后我们将0填入缺失值。得到的矩阵如图3.4右侧所示。【不进行均值矩阵的话，也就类似于我们将每一行的均值填入缺失值）

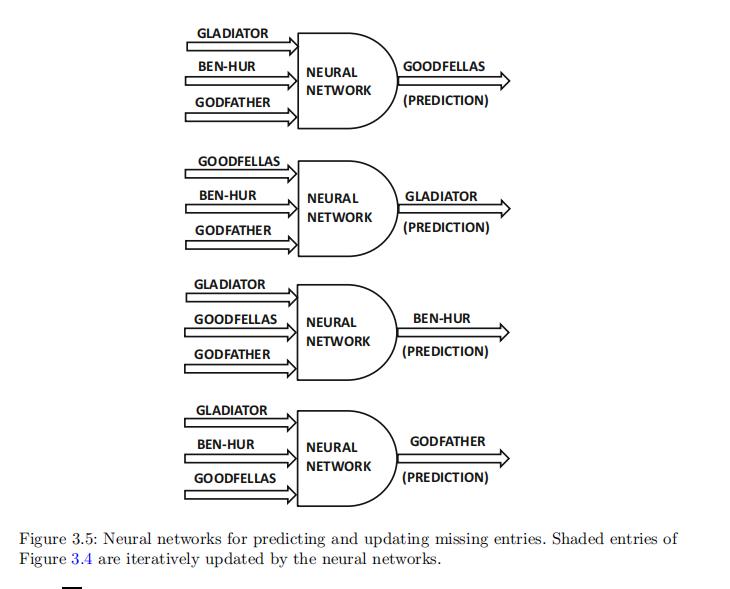
        由于有四个项目，因此有四种可能的神经网络模型，其中每个模型都是通过使用其他三个项目的评分输入作为训练列，第四个作为测试列来构建的。

        这四个神经网络如图 3.5 所示。图 3.4 的完整矩阵用于在第一次迭代中训练这些神经网络中的每一个。

        第一次迭代结束后，会使用神经网络做出的预测结果来创建一个新矩阵，其中用预测值更新缺失的条目。

        换句话说，3.4用均值补全的矩阵仅使用一次。

        更新后，图 3.4 的阴影条目将不再为零。更新后的该矩阵现在用于预测下一次迭代的条目。迭代地重复这种方法直到收敛。

        请注意，每次迭代都需要应用 n 个训练程序，其中 n 是项目数。然而，不需要在每次迭代中从头开始学习神经网络的参数。上一次迭代的参数可以作为一个很好的起点。