数据结构与算法之深入解析最优运动员比拼回合的求解思路与算法示例
Posted Forever_wj
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法之深入解析最优运动员比拼回合的求解思路与算法示例相关的知识,希望对你有一定的参考价值。
一、题目描述
- n 名运动员参与一场锦标赛,所有运动员站成一排,并根据最开始的站位从 1 到 n 编号(运动员 1 是这一排中的第一个运动员,运动员 2 是第二个运动员,依此类推)。
- 锦标赛由多个回合组成(从回合 1 开始),每一回合中,这一排从前往后数的第 i 名运动员需要与从后往前数的第 i 名运动员比拼,获胜者将会进入下一回合,如果当前回合中运动员数目为奇数,那么中间那位运动员将轮空晋级下一回合。
- 例如,当前回合中,运动员 1, 2, 4, 6, 7 站成一排:
-
- 运动员 1 需要和运动员 7 比拼;
-
- 运动员 2 需要和运动员 6 比拼;
-
- 运动员 4 轮空晋级下一回合。
- 每回合结束后,获胜者将会基于最开始分配给他们的原始顺序(升序)重新排成一排。
- 编号为 firstPlayer 和 secondPlayer 的运动员是本场锦标赛中的最佳运动员,在他们开始比拼之前,完全可以战胜任何其他运动员,而任意两个其他运动员进行比拼时,其中任意一个都有获胜的可能,因此可以裁定谁是这一回合的获胜者。
- 给出三个整数 n、firstPlayer 和 secondPlayer,返回一个由两个值组成的整数数组,分别表示两位最佳运动员在本场锦标赛中比拼的最早回合数和最晚回合数。
- 示例 1:
输入:n = 11, firstPlayer = 2, secondPlayer = 4
输出:[3,4]
解释:
一种能够产生最早回合数的情景是:
回合 1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
回合 2:2, 3, 4, 5, 6, 11
回合 3:2, 3, 4
一种能够产生最晚回合数的情景是:
回合 1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
回合 2:1, 2, 3, 4, 5, 6
回合 3:1, 2, 4
回合 4:2, 4
- 示例 2:
输入:n = 5, firstPlayer = 1, secondPlayer = 5
输出:[1,1]
解释:两名最佳运动员 1 和 5 将会在回合 1 进行比拼。
不存在使他们在其他回合进行比拼的可能
- 提示:
-
- 2 <= n <= 28
-
- 1 <= firstPlayer < secondPlayer <= n
二、求解算法
① 动态规划,妙用对称性简化计算量
- 显然每一回合人数减半,直到 first、second 相遇,以 28 人为例,每一回合的人数分别为 roundLens = [28, 14, 7, 4, 2]。
- 我们记 earliest[len][firstPlayer][secondPlayer] 表示有 len 个人,两个最强者索引分别为 firstPlayer、secondPlayer 时,最早相遇的轮次,而 latest 表示最晚相遇轮次,那么在本轮的比拼中,firstPlayer、secondPlayer 必然获胜,然后需要枚举所有其它两两比拼的胜负情况,对每一种情况,在下一轮的时候,firstPlayer、secondPlayer 会出现在一个新的位置,记作 nextFirst、nextSecond,那么 earliest[len][firstPlayer][secondPlayer] 就是所有 earliest[len / 2][nextFirst][nextSecond] 的最小值,同理 latest[len][firstPlayer][secondPlayer] 就是所有 latest[len / 2][nextFirst][nextSecond] 的最大值。
- 从小往大递推所有的 earliest 和 latest,仍以 28 为例,需要计算的长度分别为 [2, 4, 7, 14, 28]。这里和普通的动态规划不同,单个用例时并不需要计算每一个len的情况,而只需要计算 roundLens 里面的 len;当 len = 2 时,显然只有一种情况,那就是 earliest[2][0][1] = latest[2][0][1] = 1,即只有两个人,firstPlayer、secondPlayer 的索引必然只能是 0 和 1,他们俩必然在第一轮的时候相遇,所以最早、最晚都是 1。
- 接下来往大的方向递推,每一轮时枚举 firstPlayer、secondPlayer 所有可能的位置,计算出所有的 earliest 和 latest,最终 earliest[n][firstPlayer - 1][secondPlayer - 1] 就是答案。通过上面的思路可以看出,本题的难点在于每一轮确定了 len、firstPlayer、secondPlayer 之后,下一轮可能的 nextFirst、nextSecond 是哪些呢?
- 一个明显的结论是答案具有对称性,这种对称性体现在两个方面,一个是最强两人互换位置,结果是一样的,即 earliest[len][firstPlayer][secondPlayer] = earliest[len][secondPlayer][firstPlayer],这就提示我们只需要计算 secondPlayer > firstPlayer 的情况;第二个是两个人同时换到镜像点位,结果是一样的。比如有 10 个人,最强两个人的索引分别为 0 和 1,那么 0 的镜像点位是 9,1 的镜像点位是 8,所以 earliest[10][0][1] = earliest[10][9][8] = earliest[10][8][9]。
- 由以上结论,可以将所有的最强点位归纳为两种情况,以 n = 10 为例:
-
- firstPlayer 在左侧,secondPlayer 也在左侧;
-
- firstPlayer 在左侧,secondPlayer 在右侧,mirrorSecond > firstPlayer,比如 firstPlayer = 1,secondPlayer = 6,mirrorSecond = 3;
-
- firstPlayer 在左侧,secondPlayer 在右侧,mirrorSecond < firstPlayer,比如 firstPlayer = 3,secondPlayer = 8,mirrorSecond = 1,这种情况将它等价于 firstPlayer = 1, secondPlayer = 6,就变为场景 b;
-
- firstPlayer 在右侧,secondPlayer 也在右侧,通过镜像将它变为场景 a;
- 先看场景 a,firstPlayer 必将留下,firstPlayer 前面 [0, firstPlayer) 可能留下任意个,所以在下一轮,nextFirst 的可能取值为 [0, firstPlayer];secondPlayer 必将留下,区间 (firstPlayer, secondPlayer) 可能留下任意个,并且这个个数不受 firstPlayer 和它前面个数的影响,所以 nextSecond 的可能取值是 [nextFirst + 1, nextFirst + secondPlayer - firstPlayer]。
- 再看场景 b,nextFirst 的情况不变;secondPlayer 必将留下,区间 [mirrorSecond, secondPlayer] 必将留下一半,区间 (firstPlayer, mirrorSecond) 可能留下任意个,所以 nextSecond 的可能取值是 [nextFirst + (secondPlayer - mirrorSecond) / 2, nextFirst + (secondPlayer - mirrorSecond) / 2 + mirrorSecond - firstPlayer]。
- 综上,枚举所有可能的 nextFirst 和 nextSecond 的组合,earliest[len / 2][nextFirst][nextSecond] 的最小值就是 earliest[len][firstPlayer][secondPlayer]。
- C++ 示例:
class Solution
public:
vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer)
vector<int> roundLens;
vector<vector<vector<int>>> earliest(n + 1, vector<vector<int>>(n, vector<int>(n, n + 1))), latest(n + 1, vector<vector<int>>(n, vector<int>(n, 0)));
getRoundLens(n, roundLens);
for (int roundLen : roundLens)
getEarliestAndLatest(roundLen, earliest, latest);
--firstPlayer, --secondPlayer;
if (firstPlayer > secondPlayer)
swap(firstPlayer, secondPlayer);
if (firstPlayer >= n / 2 || n - secondPlayer <= firstPlayer) // 求对称位置
int tmpFirst = n - 1 - firstPlayer, tmpSecond = n - 1 - secondPlayer;
firstPlayer = tmpSecond, secondPlayer = tmpFirst;
getEarliestAndLatest(n, firstPlayer, secondPlayer, earliest, latest);
return earliest[n][firstPlayer][secondPlayer], latest[n][firstPlayer][secondPlayer] ;
void getRoundLens(int n, vector<int>& roundLens)
while (n > 2)
n = (n + 1) / 2;
roundLens.push_back(n);
reverse(roundLens.begin(), roundLens.end());
void getEarliestAndLatest(int roundLen, vector<vector<vector<int>>>& earliest, vector<vector<vector<int>>>& latest)
for (int firstPlayer = 0; firstPlayer < roundLen - 1; ++firstPlayer)
for (int secondPlayer = firstPlayer + 1; secondPlayer < roundLen; ++secondPlayer)
getEarliestAndLatest(roundLen, firstPlayer, secondPlayer, earliest, latest);
void getEarliestAndLatest(int roundLen, int firstPlayer, int secondPlayer, vector<vector<vector<int>>>& earliest, vector<vector<vector<int>>>& latest)
if (firstPlayer + secondPlayer == roundLen - 1) // 在对称位置上,第一轮必然相遇
earliest[roundLen][firstPlayer][secondPlayer] = latest[roundLen][firstPlayer][secondPlayer] = 1;
return;
// 两个数都在右侧,或者第二个数比第一个数更靠近端点,将两个数交换到对称位置
if (firstPlayer >= roundLen / 2 || roundLen - secondPlayer <= firstPlayer)
int tmpFirst = roundLen - 1 - firstPlayer, tmpSecond = roundLen - 1 - secondPlayer;
earliest[roundLen][firstPlayer][secondPlayer] = earliest[roundLen][tmpSecond][tmpFirst];
latest[roundLen][firstPlayer][secondPlayer] = latest[roundLen][tmpSecond][tmpFirst];
return;
// 下一轮,第一个数可以在区间[0, firstPlayer]任意位置
int minNextFirst = 0, maxNextFirst = firstPlayer, minNextSecond = 0, maxNextSecond = 0, halfLen = (roundLen + 1) / 2;
if (secondPlayer < (roundLen + 1) / 2) // 第二个数在左侧,则下一轮第二个数可以在第一个数后面[1, secondPlayer - firstPlayer]任意位置
minNextSecond = 1, maxNextSecond = secondPlayer - firstPlayer;
else // 第二个数在右侧,那么区间[mirrorSecondPlayer, secondPlayer]必然剩下一半,而区间(firstPlayer, mirrorSecondPlayer)可以剩下任意个数
minNextSecond = secondPlayer - (roundLen / 2 - 1), maxNextSecond = minNextSecond + roundLen - 1 - secondPlayer - firstPlayer - 1;
for (int nextFirst = minNextFirst; nextFirst <= maxNextFirst; ++nextFirst)
for (int nextSecond = minNextSecond; nextSecond <= maxNextSecond; ++nextSecond)
earliest[roundLen][firstPlayer][secondPlayer] = min(earliest[roundLen][firstPlayer][secondPlayer], earliest[halfLen][nextFirst][nextFirst + nextSecond] + 1);
latest[roundLen][firstPlayer][secondPlayer] = max(latest[roundLen][firstPlayer][secondPlayer], latest[halfLen][nextFirst][nextFirst + nextSecond] + 1);
;
- 复杂度分析:
-
- 时间复杂度:需要计算 logn 轮,每一轮枚举 firstPlayer、secondPlayer 需要 n2,枚举 nextFirst、nextSecond 需要 n2,所以总的时间复杂度是 O(logn * n4)。
- 空间复杂度:n3,尽管采用数组实现有些空间并没有使用到。
② 随机化模拟
- 为每一个运动员随机生成一个战斗力(保证 firstPlayer 和 secondPlayer 为最大和次大),当两个运动员进行比拼时战斗力较高的获胜。
- 不断模拟,统计 firstPlayer 和 secondPlayer 相遇的轮次的最大值和最小值即可。
- 如果是看所有用例的总用时,那么需要根据 n 的大小来设置模拟次数。
- C++ 示例:
struct node
int a , b;
bool operator <(const node &p)
return b < p.b;
player[30];
class Solution
public:
vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer)
srand(time(NULL));
// 根据n的大小设置模拟次数
int N;
if(n <= 10)
N = 800;
else if (n <= 20)
N = 8000;
else N = 38000;
int ans1 = 9999 , ans2 = 0 , rest , now;
while(N--)
// 剩余的运动员
rest = n;
// 初始化战斗力
for(int i = 1 ; i <= n ; i++)
player[i].a = rand() % 1075943;
player[i].b = i;
player[firstPlayer].a = 11000000;
player[secondPlayer].a = 10999999;
// 统计轮次
now = 1;
// 模拟比赛
while(rest > 1)
for(int i = 1 ; i <= rest / 2 ; i++)
if(player[i].a < player[rest + 1 - i].a)
player[i] = player[rest + 1 - i];
// 统计firstPlayer和secondPlayer相遇轮次的最大值和最小值
if(player[i].b == firstPlayer && player[rest + 1 - i].b == secondPlayer)
ans1 = min(ans1 , now) , ans2 = max(ans2 , now);
now++;
rest = (rest + 1) / 2;
sort(player + 1 , player + rest + 1);
vector<int> ans = ans1 , ans2;
return ans;
;
③ 分析本质不同的站位情况 + 记忆化搜索(Leetcode 官方解法)
- 我们可以用 F(n,f,s) 表示还剩余 n 个人,并且两名最佳运动员分别是一排中从左往右数的第 f 和 s 名运动员时,他们比拼的最早回合数。同理,我们用 G(n,f,s) 表示他们比拼的最晚回合数,那么如何进行状态转移呢?
- 如果我们单纯地用 F(n,f,s) 来进行状态转移,会使得设计出的算法和编写出的代码都相当复杂。例如我们需要考 s 也需要考虑那么多情况,这样状态转移方程就相当麻烦。
- 我们可以考虑分析出本质不同的站位情况,如下所示:
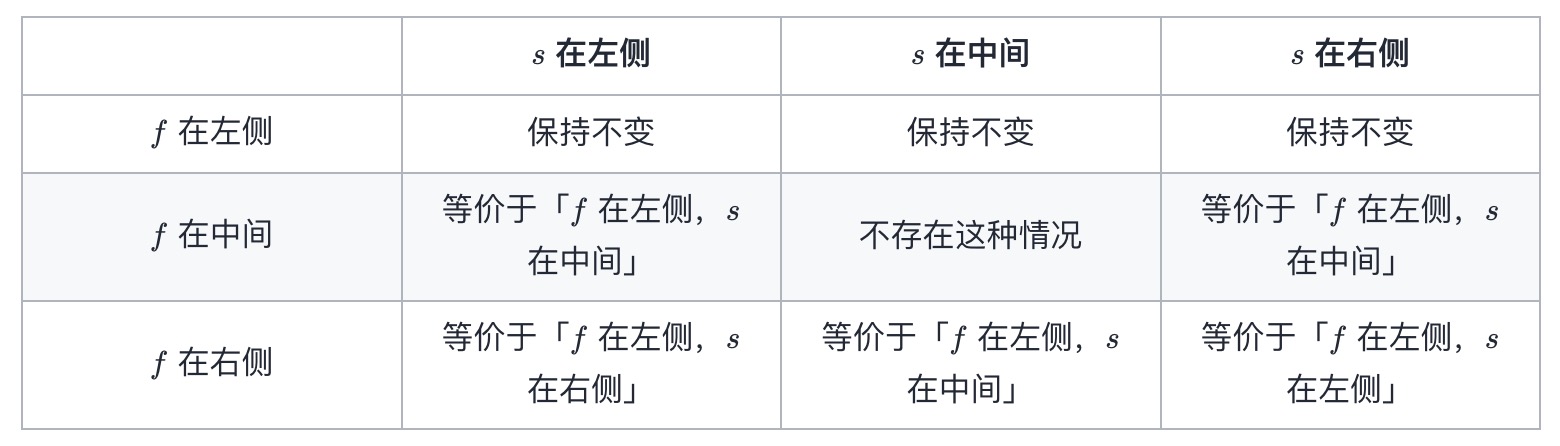
- 其正确性在于:
-
- F(n,f,s)=F(n,s,f) 恒成立,即交换两名最佳运动员的位置,结果不会发生变化;
-
- F(n,f,s)=F(n,n+1−s,n+1−f) 恒成立,因为我们会让从前往后数的第 i 运动员与从后往前数的第 i 名运动员进行比拼,那么将所有的运动员看成一个整体,整体翻转一下,结果同样不会发生变化。
- 使用这两条变换规则,就可以保证在 F(n,f,s) 中,f 一定小于 s,那么 f 一定在左侧,而 s 可以在左侧、中间或者右侧,这样我们就将原本的 8 种情况减少到了 3 种情况。对于 G(n,f,s),其做法是完全相同的。
- 既然知道 f 一定在左侧,那么就可以根据 s 在左侧、中间还是右侧,分别设计状态转移方程:如果 s 在左侧,如下图所示:
-
- f 左侧有 f−1 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 [0,f−1] 名运动员;
-
- f 与 s 中间有 s−f−1 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 [0,s−f−1] 名运动员。

- 如果 f−1 名运动员中剩下了 i 名,而 s−f−1 名运动员中剩下了 j 名,那么在下一回合中,两名最佳运动员分别位于位置 i+1 和位置 i+j+2,而剩余的运动员总数为 [(n+1)/2],其中 ⌊x⌋ 表示对 x 向下取整,因此可以得到状态转移方程:
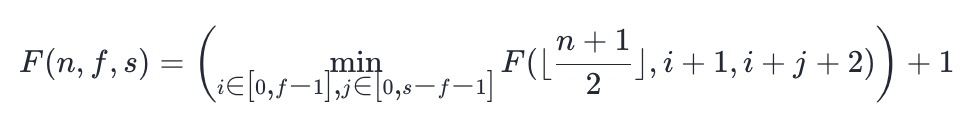
- 如果 s 在中间,如下图所示,可以发现状态转移方程与 s 在左侧的情况是完全相同的:

- 如果 s 在右侧,那么情况会较为麻烦,会有三种情况:
-
- 最简单的情况就是 f 和 s 恰好比拼,即 f+s=n+1,那么 F(n,f,s)=1;
-
- 此外,设这一回合与 s 比拼的是 s′ = n+1−s,那么 f < s′ 是一种情况,f > s′ 是另一种情况。
- 然而我们可以知道,根据类似上文中的「本质不同的站位情况」的分析,将 f 变为 n+1−s,s 变为 n+1−f,这样 f 仍然小于 s,并且 f 也小于 s′ 了,因此只需要考虑 f< s′ 的情况,如下图所示:
-
- f 左侧有 f−1 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 [0,f−1] 名运动员;
-
- f 与 s′ 中间有 s′ − f − 1 名运动员,它们会与右侧对应的运动员进行比拼,因此剩下 [0,s′ −f−1] 名运动员;
-
- s′ 一定会输给 s;
-
- s′ 与 s 中间有 n−2s′ 名运动员,如果 n−2s′ 是偶数,那么他们两两之间比拼,剩下 (n−2s′)/2 名运动员;如果 n−2s′ 是奇数,那么其中一人轮空,剩余两两之间比拼,剩下 (n−2s′+1)/2 名运动员,因此,无论 n−2s′ 是奇数还是偶数,s′ 与 s 中间一定会有 ⌊(n−2s′+1)/2⌋ 名运动员。

- 如果 f−1 名运动员中剩下了 i 名,而 s′−f−1 名运动员中剩下了 j 名,那么在下一回合中,两名最佳运动员分别位于位置 i+1 和位置 i+j+⌊(n−2s′+1)/2⌋+2,因此可以得到状态转移方程:
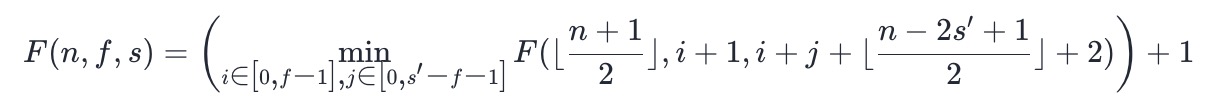
- 这样就得到了所有关于 F 的状态转移方程,而关于 G 的状态转移方程,只需要把所有的 min 改为 max 即可。
- 根据上文中的两种变换规则,具体应当在 n,f,s 满足什么关系(而不是抽象的「左侧」「中间」「右侧」)时使用其中的哪些规则呢?这里有很多种设计方法,举一种较为简单的,题解代码中使用的方法:
-
- 首先我们使用自顶向下的记忆化搜索代替动态规划进行状态转移,这样写更加简洁直观,并且无需考虑状态的求值顺序;
-
- 记忆化搜索的入口为 F(n,firstPlayer,secondPlayer),在开始记忆化搜索之前,先通过变换规则 F(n,f,s)=F(n,s,f) 使得 firstPlayer 一定小于 secondPlayer,这样一来,由于另一条变换规则 F(n,f,s)=F(n,n+1−s,n+1−f) 不会改变 f 与 s 间的大小关系,因此在接下来的记忆化搜索中,f<s 是恒成立的,我们也就无需使用变换规则 F(n,f,s)=F(n,s,f);
-
- 在上文中的表格中,我们需要变换的情况有 5 种,分别是:「f 在中间,s 在左侧」「f 在中间,s 在右侧」「f 在右侧,s 在左侧」「f 在右侧,s 在中间」「f 在右侧,s 在右侧」,由于已经保证了 f<s 恒成立,因此这 5 种情况中只剩下 2 种是需要处理的,即:「f 在中间,s 在右侧」和「f 在右侧,s 在右侧」。此外,我们在「状态转移方程的设计」一节中还发现了一种需要处理的情况,即「f 在左侧,s 在右侧,并且 f > s′ =n+1−s」。那么这 3 种情况是否可以统一呢?对于最后一种情况,我们有 f+s > n+1,而「f 在中间,s 在右侧」和「f 在右侧,s 在右侧」也恰好满足 f+s > n+1,并且所有不需要变换的情况都不满足 f+s > n+1,因此只需要在 f+s > n+1 时,使用一次变换规则 F(n,f,s)=F(n,n+1−s,n+1−f) 就行了。
- 由于 Python 中可以很方便地使用 @cache 进行记忆化搜索,因此在下面 Python 的代码中,无需显式地定义 F 和 G,函数 dp(n,f,s) 返回的二元组即为 F(n,f,s) 和 G(n,f,s),示例如下:
class Solution:
def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:
@cache
def dp(n: int, f: int, s: int) -> (int, int):
if f + s == n + 1:
return (1, 1)
# F(n,f,s)=F(n,n+1-s,n+1-f)
if f + s > n + 1:
return dp(n, n + 1 - s, n + 1 - f)
earliest, latest = float("inf"), float("-inf")
n_half = (n + 1) // 2
if s <= n_half:
# s 在左侧或者中间
for i in range(f):
for j in range(s - f):
x, y = dp(n_half, i + 1, i + j + 2)
earliest = min(earliest, x)
latest = max(latest, y)
else:
# s 在右侧
# s'
s_prime = n + 1 - s
mid = (n - 2 * s_prime + 1) // 2
for i in range(f):
for j in range(s_prime - f):
x, y = dp(n_half, i + 1, i + j + mid + 2)
earliest = min(earliest, x)
latest = max(latest, y)
return (earliest + 1, latest + 1)
# F(n,f,s) = F(n,s,f)
if firstPlayer > secondPlayer:
firstPlayer, secondPlayer = secondPlayer, firstPlayer
earliest, latest = dp(n, firstPlayer, secondPlayer)
dp.cache_clear()
return [earliest, latest]
- C++ 示例:
class Solution
private:
int F[30][30][30], G[30][30][30];
public:
pair<int, int> dp(int n, int f, int s)
if (F[n][f][s])
return F[n][f][s], G[n][f][s];
if (f + s == n + 1)
return 1, 1;
// F(n,f,s)=F(n,n+1-s,n+1-f)
if (f + s > n + 1)
tie(F[n][f][s], G[n][f][s]) = dp(n, n + 1 - s, n + 1 - f);
return F[n][f][s], G[n][f][s];
int earlist = INT_MAX, latest = INT_MIN;
int n_half = (n + 1) / 2;
if (s <= n_half)
// 在左侧或者中间
for (int i = 0; i < f; ++i)
for (int j = 0; j < s - f; ++j)
auto [x, y] = dp(n_half, i + 1, i + j + 2);
earlist = min(earlist, x);
latest = max(latest, y);
else
// s 在右侧
// s'
int s_prime = n + 1 - s;
int mid = (n - 2 * s_prime + 1) / 2;
for (int i = 0; i < f; ++i)
for (int j = 0; j < s_prime - f; ++j)
auto [x, y] = dp(n_half, i + 1, i + j + mid + 2);
earlist = min(earlist, x);
latest = max(latest, y);
return F[n][f][s] = earlist + 1, G[n][f][s] = latest + 1;
vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer)
memset(F, 0, sizeof(F));
memset(G, 0, sizeof(G));
// F(n,f,s) = F(n,s,f)
if (firstPlayer > secondPlayer)
swap(firstPlayer, secondPlayer);
auto [earlist, latest] = dp(n, firstPlayer, secondPlayer);
return earlist, latest;
;
- 复杂度分析:
-
- 时间复杂度:O(n4logn)。在状态 F(n,f,s) 中(G(n,f,s) 同理),每一维的范围都是 O(n),而每一个状态需要 O(n2) 的时间枚举所有可以转移而来的状态,因此整个算法的时间复杂度为 O(n5)。然而可以发现,F(n,f,s) 中的 n 的取值个数是有限的,在记忆化搜索的过程中,n 会变成 ⌊(n+1)/2⌋ 后继续向下递归,因此 n 的取值个数只有 O(logn) 种,即总时间复杂度为 O(n4logn)。
-
- 空间复杂度:O(n2logn) 或 O(n3),即为存储所有状态需要的空间。在 C++ 代码中,使用数组存储所有状态,即使 n 的取值个数只有 O(logn) 种,还是需要对第一维开辟 O(n) 的空间。而在 Python 代码中,@cache 使用元组 tuple 作为字典 dict 的键来存储所有状态的值,状态的数量为 O(n2logn),那么使用的空间也为 O(n2logn)。
以上是关于数据结构与算法之深入解析最优运动员比拼回合的求解思路与算法示例的主要内容,如果未能解决你的问题,请参考以下文章