数据结构与算法之深入解析合并两个有序数组的求解思路与算法示例

Posted 2022-01-12 Forever_wj

一、题目描述

• 给你两个按“非递减顺序”排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目，请合并 nums2 到 nums1 中，使合并后的数组同样按“非递减顺序”排列。
• 注意：最终合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略，nums2 的长度为 n 。
• 示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6]
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素

• 示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 []
合并结果是 [1]

• 示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1]
合并结果是 [1]
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中

二、求解算法

① 直接合并后排序

• 最直观的方法是先将数组 nums2 放进数组 nums1 的尾部，然后直接对整个数组进行排序；
• C 示例：

int cmp(int* a, int* b) 
    return *a - *b;


void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) 
    for (int i = 0; i != n; ++i) 
        nums1[m + i] = nums2[i];
    
    qsort(nums1, nums1Size, sizeof(int), cmp);

• C++ 示例：

class Solution 
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) 
        for (int i = 0; i != n; ++i) 
            nums1[m + i] = nums2[i];
        
        sort(nums1.begin(), nums1.end());
    
;

• 复杂度分析
• • 时间复杂度：O((m+n)log(m+n))，排序序列长度为 m+n，套用快速排序的时间复杂度即可，平均情况为
    O((m+n)log(m+n))。
• • 空间复杂度：O(log(m+n))，排序序列长度为 m+n，套用快速排序的空间复杂度即可，平均情况为 O(log(m+n))。

② 从后向前数组遍历

• 因为 nums1 的空间都集中在后面，所以从后向前处理排序的数据会更好，节省空间，一边遍历一边将值填充进去；
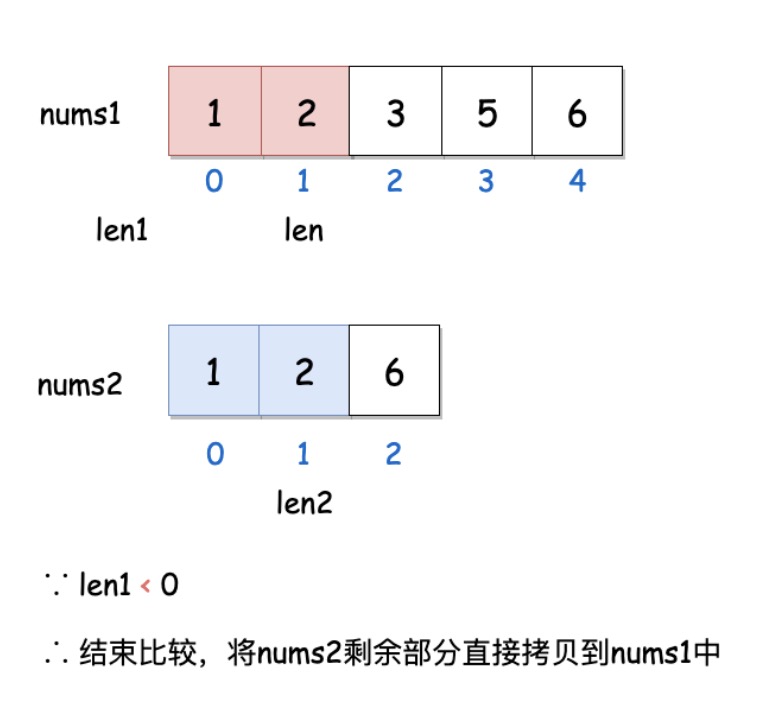
• 设置指针 len1 和 len2 分别指向 nums1 和 nums2 的有数字尾部，从尾部值开始比较遍历：

• 同时设置指针 len 指向 nums1 的最末尾，每次遍历比较值大小之后，则进行填充；

• 当 len1<0 时遍历结束，此时 nums2 中海油数据未拷贝完全，将其直接拷贝到 nums1 的前面，最后得到结果数组：

• Java 示例：

class Solution 
    public void merge(int[] nums1, int m, int[] nums2, int n) 
        int len1 = m - 1;
        int len2 = n - 1;
        int len = m + n - 1;
        while(len1 >= 0 && len2 >= 0) 
            // 注意--符号在后面，表示先进行计算再减1，这种缩写缩短了代码
            nums1[len--] = nums1[len1] > nums2[len2] ? nums1[len1--] : nums2[len2--];
        
        // 表示将nums2数组从下标0位置开始，拷贝到nums1数组中，从下标0位置开始，长度为len2+1
        System.arraycopy(nums2, 0, nums1, 0, len2 + 1);
    

③ 双指针（Leetcode 官方解法）

• 使用双指针方法，将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。如下面的动画所示：

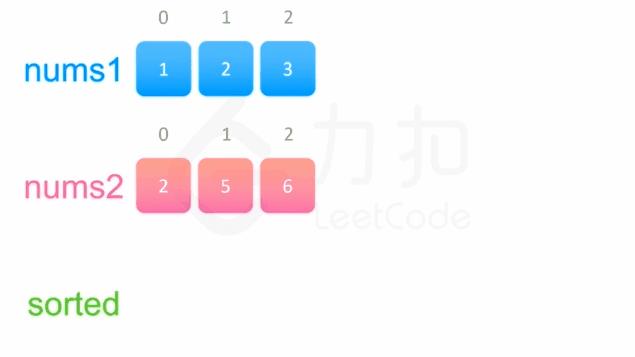
• 为两个数组分别设置一个指针 p1 与 p2 来作为队列的头部指针。
• C++ 示例：

class Solution 
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) 
        int p1 = 0, p2 = 0;
        int sorted[m + n];
        int cur;
        while (p1 < m || p2 < n) 
            if (p1 == m) 
                cur = nums2[p2++];
             else if (p2 == n) 
                cur = nums1[p1++];
             else if (nums1[p1] < nums2[p2]) 
                cur = nums1[p1++];
             else 
                cur = nums2[p2++];
            
            sorted[p1 + p2 - 1] = cur;
        
        for (int i = 0; i != m + n; ++i) 
            nums1[i] = sorted[i];
        
    
;

• C 示例：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) 
    int p1 = 0, p2 = 0;
    int sorted[m + n];
    int cur;
    while (p1 < m || p2 < n) 
        if (p1 == m) 
            cur = nums2[p2++];
         else if (p2 == n) 
            cur = nums1[p1++];
         else if (nums1[p1] < nums2[p2]) 
            cur = nums1[p1++];
         else 
            cur = nums2[p2++];
        
        sorted[p1 + p2 - 1] = cur;
    
    for (int i = 0; i != m + n; ++i) 
        nums1[i] = sorted[i];
    

• 复杂度分析：
• • 时间复杂度：O(m+n)，指针移动单调递增，最多移动 m+n 次，因此时间复杂度为 O(m+n)。
• • 空间复杂度：O(m+n)，需要建立长度为 m+n 的中间数组 sorted。