最小生成树算法——kruskal

Posted 2022-01-11 爱敲代码的Harrison

Kruskal

什么K算法，K算法就是最小生成树算法。具体说来，就是对于一张已经存在的图，如下图，

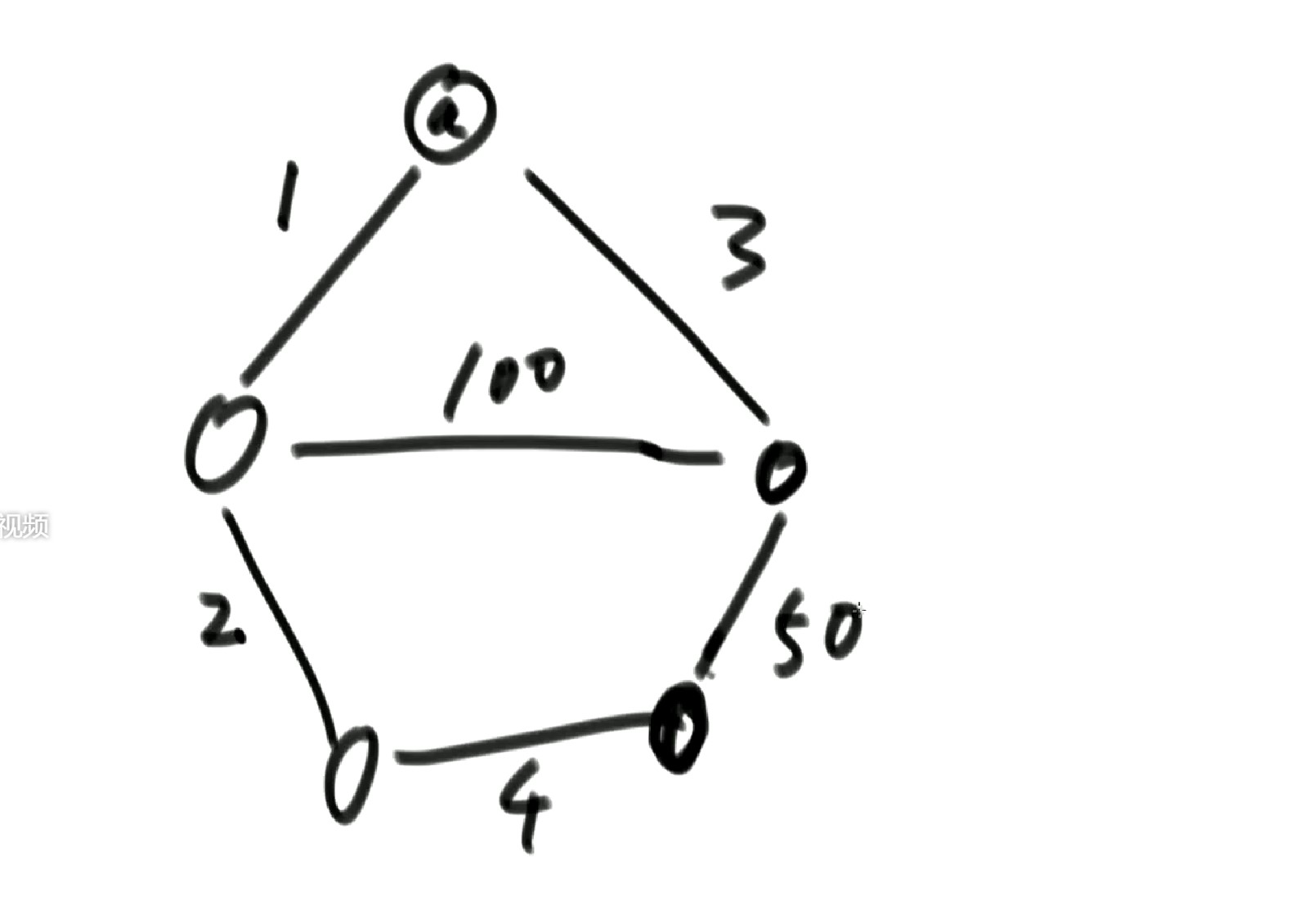
**在不破坏连通性的情况下，只留下整体权重最小的边的集合。就是边的权值加起来最小。**拿上面图举例，把权值100和50的边去掉就达到了我们的要求（所有可能性中，边的权值加起来最小的情况）：

算法流程

先把所有的边根据权值由小到大排序。假设图中每个结点都是一个单独的集合，从权值小的边开始选，如果有多条权值一样的边，无论先选哪条都行，选中某条边后，看这条边两边的点有没有在同一个集合里面，没有在一个集合里，就选上这条边，并把两侧结点归在同一个集合里面；如果这条边两边的结点在一个集合里，就不选这条边。一直到整个图联通在一起。

通过上面的分析，很明显，用并查集来做是最方便的，并查集就是解决两大片联通在一起的问题。

如果用户提供有向图，那这个算法肯定没有问题，如果是无向图呢？——那就只是边集合少了一侧，整体权重是没有变化的。

我们再来明确一点，有向图和无向图是可以认为没有明确界限的，无向图就可以认为是两边都有向。所以kruskal算法无论有向无向都可以。

最后再总结一下K算法的大概步骤：

注意：不能破环连通性！！！

1)总是从权值最小的边开始考虑，依次考察权值变大的边

2)当前的边要么进入最小生成树的集合，要么丢弃

3)如果当前的边进入最小生成树的集合中不会形成环，就要当前边,

4)如果当前的边进入最小生成树的集合中会形成环，就不要当前边

5)考察完所有边之后，最小生成树的集合也得到了

package com.harrison.class11;

import java.util.Collection;
import java.util.Comparator;
import java.util.HashMap;
import java.util.HashSet;
import java.util.PriorityQueue;
import java.util.Set;
import java.util.Stack;

import com.harrison.class11.Code01_NodeEdgeGraph.*;

public class Code05_Kruskal 
	public static class UnionFind
		// key 某一个结点	value：某一个结点往上的结点
		private HashMap<Node, Node> fatherMap;
		// key 某一个集合的代表点		value：key所在集合的结点个数
		private HashMap<Node, Integer> sizeMap;
		
		public UnionFind() 
			fatherMap=new HashMap<Node,Node>();
			sizeMap=new HashMap<Node, Integer>();
		
		
		// 一开始图中每个结点自己单独成为一个集合
		public void makeSets(Collection<Node> nodes) 
			fatherMap.clear();
			sizeMap.clear();
			for(Node node:nodes) 
				fatherMap.put(node, node);
				sizeMap.put(node, 1);
			
		
		
		public Node findFather(Node n) 
			Stack<Node> path=new Stack<>();
			while(n!=fatherMap.get(n)) 
				path.add(n);
				n=fatherMap.get(n);
			
			while(!path.isEmpty()) 
				fatherMap.put(path.pop(), n);
			
			return n;
		
		
		public boolean isSameSet(Node a,Node b) 
			return findFather(a)==findFather(b);
		
		
		public void union(Node a,Node b) 
			if(a==null || b==null) 
				return ;
			
			Node aHead=findFather(a);
			Node bHead=findFather(b);
			if(aHead!=bHead) 
				int aSetSize=sizeMap.get(aHead);
				int bSetSize=sizeMap.get(bHead);
				Node big=aSetSize>=bSetSize?aHead:bHead;
				Node small=big==aHead?bHead:aHead;
				fatherMap.put(small, big);
				sizeMap.put(big, aSetSize+bSetSize);
				sizeMap.remove(small);
			
		
	
	
	public static class EdgeComparator implements Comparator<Edge>
		public int compare(Edge e1,Edge e2) 
			return e1.weight=e2.weight;
		
	
	
	public static Set<Edge> kruskalMST(Graph graph)
		UnionFind unionFind=new UnionFind();
		unionFind.makeSets(graph.nodes.values());
		PriorityQueue<Edge> pq=new PriorityQueue<>();
		for(Edge edge:graph.edges) 
			pq.add(edge);
		
		Set<Edge> ans=new HashSet<>();
		while(!pq.isEmpty()) 
			Edge edge=pq.poll();
			if(!unionFind.isSameSet(edge.from, edge.to)) 
				ans.add(edge);
				unionFind.union(edge.from, edge.to);
			
		
		return ans;