神经网络学习中的SoftMax与交叉熵
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了神经网络学习中的SoftMax与交叉熵相关的知识,希望对你有一定的参考价值。

简 介: 对于在深度学习中的两个常见的函数SoftMax,交叉熵进行的探讨。在利用paddle平台中的反向求微分进行验证的过程中,发现结果 与数学定义有差别。具体原因还需要之后进行查找。
关键词: 交叉熵,SoftMax
在深度学习网络中,SoftMax 以及Cross Entropy(交叉熵)是最常见到神经网络输出级的数据处理以及计算损失函数。
§01 定 义
1.1 函数
SoftMax函数往往使用在分类神经网络的最后一层的处理中,它将分类神经网络的输出转换成网络对于输入样本所属类别的概率。
1.1.1 类别概率
如果神经网络 N ( φ ; X ) N\\left( \\varphi ;X \\right) N(φ;X)在输入样品 x i x_i xi的作用下,输出输出向量为 [ z 1 , z 2 , ⋯ , z M ] \\left[ z_1 ,z_2 , \\cdots ,z_M \\right] [z1,z2,⋯,zM]。分别表示该样本属于 1 ~ M 个类别的概率。但属于概率必须满足:
- z i ≥ 0 , i = 1 , 2 , ⋯ , M z_i \\ge 0,\\,\\,i = 1,2, \\cdots ,M zi≥0,i=1,2,⋯,M
- ∑ i = 1 M z i = 1 \\sum\\limits_i = 1^M z_i = 1 i=1∑Mzi=1
为了达到概率条件,需要进行处理。SoftMax处理方式是其中一种。
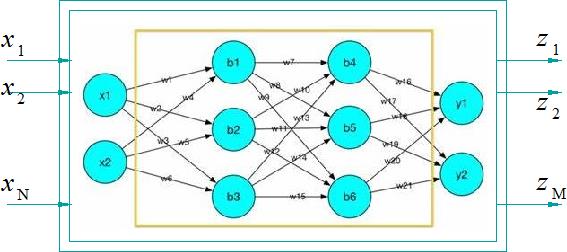
▲ 图1.1.1 神经网络输入输出示意图
1.1.2 SoftMax
在 详解softmax函数以及相关求导过程 中,给出了SoftMax的定义:
y i = e z i ∑ i = 1 M e z i y_i = e^z_i \\over \\sum\\limits_i = 1^M e^z_i yi=i=1∑Meziezi
数据计算过程中的流程图参见下图:
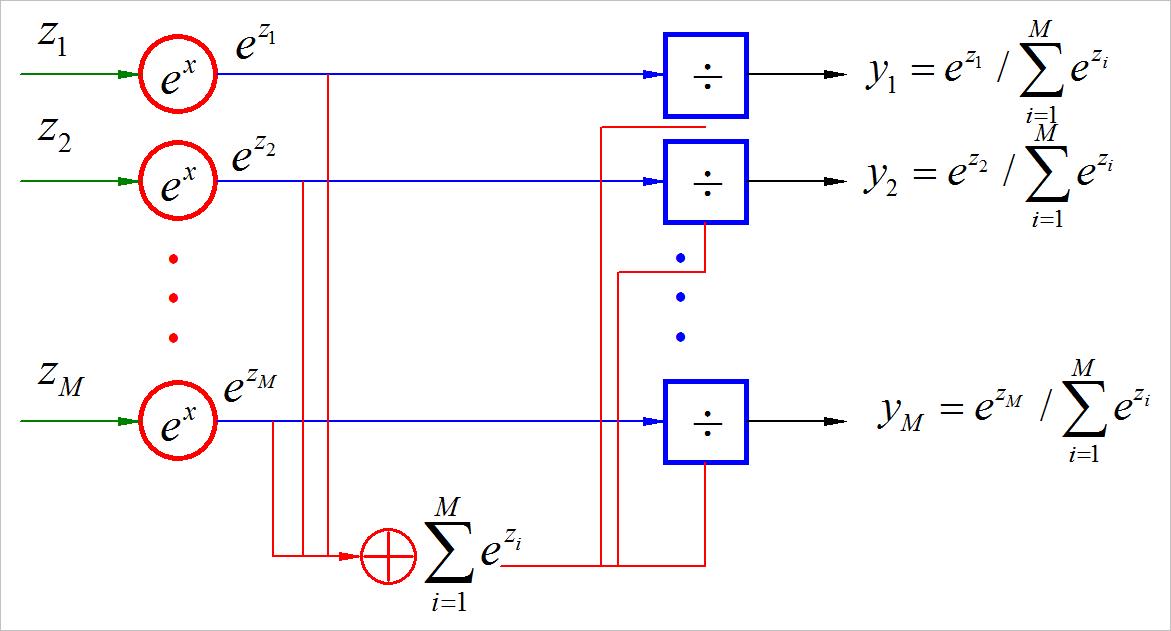
▲ 图1.1.2 SoftMax结构示意图
可以看到输出的 y i , i = 1 , 2 , ⋯ , M y_i ,i = 1,2, \\cdots ,M yi,i=1,2,⋯,M满足:
- y i ≥ 0 , i = 1 , 2 , ⋯ , M y_i \\ge 0,\\,\\,i = 1,2, \\cdots ,M yi≥0,i=1,2,⋯,M
- ∑ i = 1 M y i = 1 \\sum\\limits_i = 1^M y_i = 1 i=1∑Myi=1
(1)举例
a = [0.1,0.2,0.3,-1,5]
b = sum([exp(aa) for aa in a])
c = [exp(aa)/b for aa in a]
print("a: ".format(a), "b: :0.2f".format(b), "c: ".format(c))
a: [0.1, 0.2, 0.3, -1, 5]
b: 152.46
c: [0.007249044016189045, 0.008011432630542426, 0.008854002355397775, 0.0024129971374439265, 0.9734725238604267]
1.2 交叉熵
根据 一文搞懂熵(Entropy),交叉熵(Cross-Entropy)中的定义,对于一组样本所出现的概率分布:
p
i
,
i
=
1
,
2
,
⋯
,
M
p_i ,\\,\\,i = 1,2, \\cdots ,M
pi,i=1,2,⋯,M,所对应的信息熵为:
E
e
n
t
r
o
p
y
(
P
)
=
E
(
P
)
=
−
∑
i
=
1
M
p
i
log
(
p
i
)
E_entropy \\left( P \\right) = E\\left( P \\right) = - \\sum\\limits_i = 1^M p_i \\log \\left( p_i \\right)
Eentropy(P)=E(P)以上是关于神经网络学习中的SoftMax与交叉熵的主要内容,如果未能解决你的问题,请参考以下文章