二叉树深入剖析

Posted 2022-01-08 时空旅客～

文章目录

• • **二叉树的遍历（前序，中序，后序）**
  • 计算二叉树的节点的个数
  • 计算第k层的节点
  • 二叉树的深度
  • 查找一个节点
  • 层序遍历
  • 判断是否为完全二叉树
  • test.c

二叉树的基本结构

用指针来指向两个子树节点，依次来把节点来连接起来

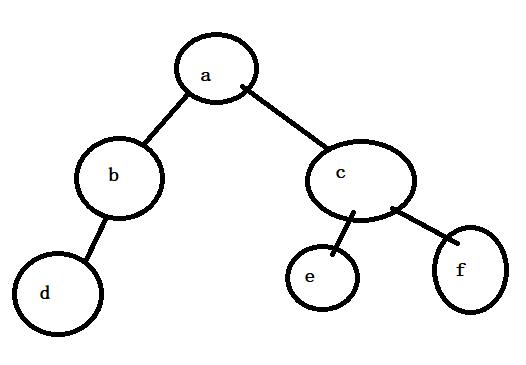
二叉树的遍历（前序，中序，后序）

#include<stdio.h>
#include<stdlib.h>
typedef char btdata;

typedef struct BinaryTreeNode

    //指针域
    struct BinaryTreeNode *left;//链接左孩子
    struct BinaryTreeNode *right;//链接右孩子
    btdata data;//数据域
btnode;


//开辟节点
btnode* buynode(btdata x)

    

    btnode*node=malloc(sizeof(btnode));
    if(node==NULL)//判定是否动态开辟成功
    
        exit(-1);//没开辟成功就退出
    

node->data=x;//链接数据
node->left=NULL;//还没链接其他指针就置成空
node->right=NULL;



//暴力造一个树
btnode*creatbinarytree()


    btnode*nodeA=buynode('A');
    btnode*nodeB=buynode('B');
    btnode*nodeC=buynode('C');
    btnode*nodeD=buynode('D');
    btnode*nodeE=buynode('E');
    btnode*nodeF=buynode('F');
    nodeA->left=nodeB;
    nodeB->left=nodeD;
    nodeA->right=nodeC;
    nodeC->left=nodeE;
    nodeC->right=nodeF;
    return nodeA;//返回的是根节点


//前序
void preorder(btnode*root)

    //如果当前三一个空树
    if(root==NULL)
    
        printf("NULL->");
        return ;
    
//不是一个空树
printf("%c->",root->data);//先遍历根，后再遍历左右
preorder(root->left);//左子树
preorder(root->right);//右子树



//中序   左根右
void inorder(btnode*root)

    //如果当前三一个空树
    if(root==NULL)
    
        printf("NULL->");
        return ;
    
//不是一个空树

inorder(root->left);//左子树
printf("%c->",root->data);//根
inorder(root->right);//右子树


//后序   左右根
void postorder(btnode*root)

    //如果当前三一个空树
    if(root==NULL)
    
        printf("NULL->");
        return ;
    
//不是一个空树

postorder(root->left);//左子树
postorder(root->right);//右子树
printf("%c->",root->data);//根

计算二叉树的节点的个数

//一.计算节点的个数
//错误方法
int binarytreesize(btnode*root)

    if(root==NULL)
    
        return 0;
    
    static int count=0;//用了static的话，每次调用都会在原来的基础上对count进行++，
    //如果不加static的话，cout在栈上开辟，调用完就会销毁
    count++;
    binarytreesize(root->left);
    binarytreesize(root->right);
    return count;//这样计算出来的结果永远都是1


//正确的做法1.
void binarytreesize2(btnode*root,int*x)//用指针进行操作，这样每次都是对同一个空间进行操作

    if(root==NULL)
    
        return;
    
    ++(*x);//对地址进行操作就不会出现static和销毁的情况了
    binarytreesize2(root->left,x);
    binarytreesize2(root->right,x);

//正确的做法2.
int binarytreesize3(btnode*root)

    return root==NULL?0:binarytreesize3(root->left)+binarytreesize3(root->right)+1;//把问题分为了左右子树，和自己，不断的细分，左右+1

//二.计算叶子节点的个数，就是没有子树节点的个数，度为0的个数

int binaryleafsize2(btnode*root)//左子树的叶子节点和右子树的叶子节点加起来

if(root==NULL)//并非一定整个树都是空，后面递归可能三左子树或右子树是空

return 0;


    return (root->left==NULL)&&(root->right==NULL)?1:binaryleafsize2(root->left)+binaryleafsize2(root->right);//叶子节点左右都没有节点，则+1，为叶子就返回一，不为叶子就继续把左右子树的叶子加起来

在这里插入代码片

计算第k层的节点

//三.计算第k层节点的个数
//如，要求第4层，就求的3层的左子树节点数量加上右子树第3层的节点

//这里我们用了一个相对距离的概念
int binarytreelevelsize(btnode*root,int k)

 if(root==NULL)//没有节点，就通通返回0
 
     return 0;
 
 if(k<1)
 
     return 0;
 
 //走到了这里，就不为空
 else if(k==1)
 
     return 1;//如果要我们求第一层就返回1,不用求了
 
//root不为空，k大于1
//说明root第k层的节点在子树里面，
//就转化为了左右子树的第k-1层节点的数量
//如要求我的第4层，相当于求为左子树的第三层和右子树的第3层,
//直到为第一层，本层
return binarytreelevelsize(root->left,k-1)+binarytreelevelsize(root->right,k-1);

```c

二叉树的深度

//计算树的深度（高度）层次
//我们一般规定第一层为1，空树就算0,从1开始
//计算深度就是左子树深度和右子树深度中大的+1
int binarytreedepth(btnode*root)

if(root==NULL)

    return 0;

//这样写会重复计算，因为前面比较的时候已经算出结果了，但因为没有保存结果，严重的浪费了，
//return binarytreedepth(root->left)>binarytreedepth(root->right)?binarytreedepth(root->left)+1:binarytreedepth(root->right)+1;//大的那个+1

//用一个变量来记录
int leftdepth=binarytreedepth(root->left);//一层一层留一个大的返回区
int rightdepth=binarytreedepth(root->right);
//相当于后序
return leftdepth>rightdepth?leftdepth+1:rightdepth+1;






```c

查找一个节点

//二叉树中查找值为x的节点
//找到了就返回他的地址
btnode* binarytreefind(btnode*root,btdata x)

//根左右的遍历
//先找根
if(root==NULL)

    return NULL;//返回null是为了告诉上一层我没找到

if(root->data==x)//找到了

    return root;

      btnode*leftret=binarytreefind(root->left,x);
      if(leftret)//不为空，也就是左边找到了
      
            return leftret;
      
    btnode*rightret=binarytreefind(root->right,x);
     if(rightret)//没走上面的就走下面的，右边找到了
     
      return rightret;
     
return NULL;//左边没找到，右边也没找到

层序遍历

用队列实现
1.先入根
2.在当前节点出来后，再把他的左右孩子带进去，不为空才带进去，这样上一层节点出的时候，带入下一层
3.直到队列为空，说明最后一层没有节点，遍历结束

void binarytreelevelorder(btnode* root)

	if (root == NULL)//必须的操作
		return;

	queue q;
	queueinit(&q);//初始化一个队列
	queuepush(&q, root);//入队
	while (!queueempty(&q))//队不为空就继续操作
	
		btnode* front = queuefront(&q);//取下队头，避免之后找不到队里面的数据
		queuepop(&q);//出队
		printf("%c ", front->data);//打印

		// 孩子带进队列
		if (front->left)
			queuepush(&q, front->left);//左右孩子不为空就入

		if (front->right)
			queuepush(&q, front->right);
	
	printf("\\n");

	//queuedestroy(&q);

判断是否为完全二叉树

判断满二叉树，可以计算树的高度，再计算树的节点树，是否等于2^h-1,十分容易

1.判断是否是完全二叉树(非空节点是连续的)
用层序遍历，队列的时候，空也入，null也当作一个元素，遇到空之后，队列里面全是空
非完全二叉树，遇到空后，队列里面并非全空

bool iscompletebinarytree(btnode*root)

    queue q;
    queueinit(&q);
    queuepush(&q, root);
    while (!queueempty(&q))//不为空就进入//队头
    
        btnode* front = queuefront(&q);
        //空也进
        queuepop(&q);
        if (front == NULL)//遇到了一个NULL元素就跳出去，ci
        
            //为空的花就跳出去
            break;
        
        else
        
            //front不为空就入左右，左右不管是否为空都入，NULL也是元素
            queuepush(&q, front->left);
            queuepush(&q, front->right);
        
        
    
    //跳出去检查剩下的节点是否全是空,剩下的全是空就是完全二叉树，存在非空，则是非完全二叉树，
    //出剩下的所有节点
    while (queuesize(&q))//null也当作一个元素，直到元素个数完了，就是全是空的
    
         btnode* front = queuefront(&q);
        queuepop(&q);
        if (front)//遇到了不为空
        
            queuedestroy(&q);
            return false;
        

    
    queuedestroy(&q);
    return true;

test.c

int main()

    btnode*root=creatbinarytree();//造一个树
   // preorder(root);//前序遍历，根，左子树，右子树
    //用分治，：分而治之，大事化小，小事化了
    //如校长想知道学校有多少人，让10个院报人数，院让专业老师统计人数，老师叫班长，一步一步化小，
   //inorder(root);
     postorder(root);
     int n1=0;
     binarytreesize2(root, &n1);//把n1地址传过去，每次都对这个地址进行操作，就没有销毁的问题了
     printf("\\n");
     printf("n1=%d\\n",n1);
     int n2=0;
    printf("n2=%d\\n",binarytreesize3(root));
     int leafn=0;;
    printf("leafn=%d\\n",leafn);
    printf("leaf2=%d\\n",binaryleafsize2(root));
    int n3=0;
    printf("levelk=%d\\n",binarytreelevelsize(root,3));
printf("depth=%d\\n",binarytreedepth(root));

    return 0;