室友深深爱上了二叉树，学会了二叉树内心的深度

Posted 2022-01-08 未见花闻

⭐️前面的话⭐️

大家好！本篇文章将介绍的剑指offerOJ题，来自力扣剑指 Offer 55 - I. 二叉树的深度题解，本文将以这道题为背景介绍有关二叉树深度的知识，展示代码语言暂时为：Java，C/C++。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2021年12月20日🌴
✉️坚持和努力一定能换来诗与远方！
💭刷题推荐书籍：📚《剑指offer专项版》，📚《剑指offer第2版》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🙏作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

---

📌导航小助手📌

• ⭐️剑指 Offer 55 - I. 二叉树的深度⭐️
• • 🔐题目详情
  • 💡解题思路
  • 🔑源代码
• 🌱总结

---

---

⭐️剑指 Offer 55 - I. 二叉树的深度⭐️

🔐题目详情

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \\
  9  20
    /  \\
   15   7

返回它的最大深度 3 。

来源：力扣（LeetCode）链接：剑指 Offer 55 - I. 二叉树的深度

💡解题思路

预备知识：

问题1：什么是树？

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

树：$T=D，R$。$D$是包含n个结点的有限集合（n≥0）。当n=0时为空树，否则关系R满足以下条件:
有且仅有一个结点$d_0\in D$，它对于关系R来说没有前驱结点，结点$d_0$称作树的根结点。
除根结点外，每个结点有且仅有一个前驱结点。
$D$中每个结点可以有零个或多个后继结点。

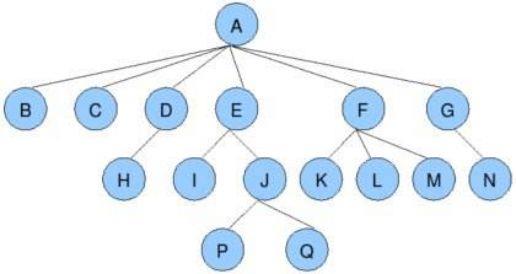
• 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6。
• 叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点。
• 非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点。
• 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点。
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点。
• 兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点。
• 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6。
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
• 树的高度或深度：树中节点的最大层次； 如上图：树的高度为4。
• 有序树和无序树：若树中各结点的子树是按照一定的次序从左向右安排的，且相对次序是不能随意变换的，则称为有序树，否则称为无序树。
• 堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点。
• 节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先。
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙。

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
子树的左结点表示孩子，右节点表示兄弟，简称“左孩子右兄弟”。

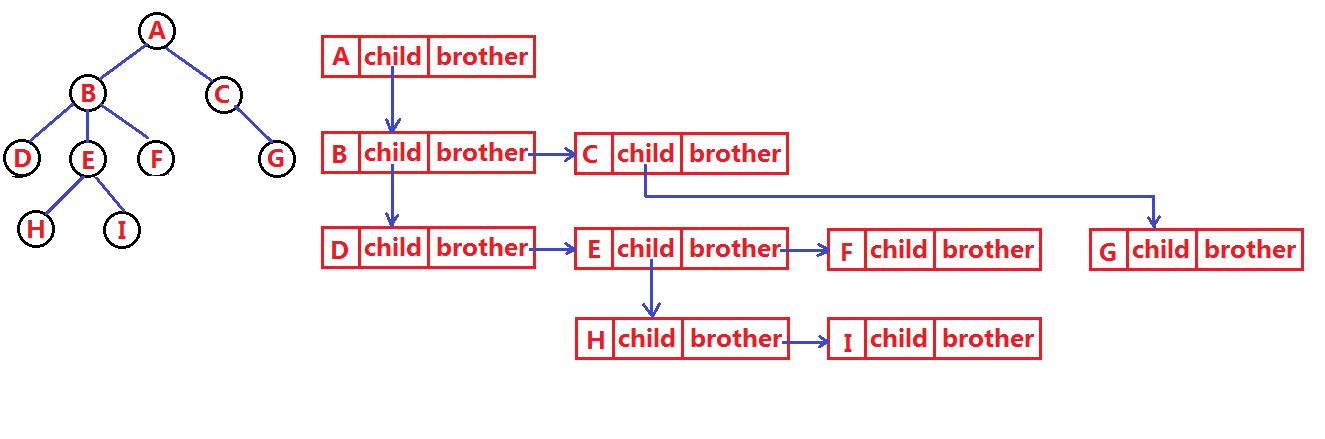
public class TreeNode 
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode(int x)  val = x; 

问题2：:什么是二叉树？
一棵二叉树是结点的一个有限集合，该集合:

1. 为空树。
2. 由一个根节点加上两棵别称为左子树和右子树的子二叉树组成。
3. 二叉树结点的度不超过2。

二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树。

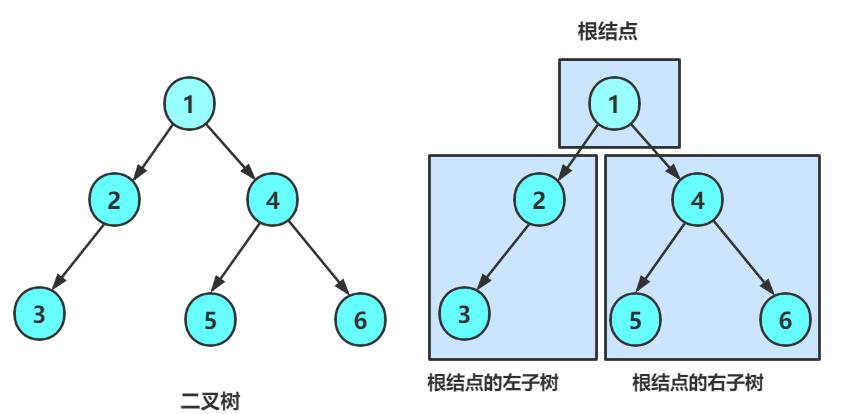
对于任意的二叉树都是由以下几种情况复合而成的：

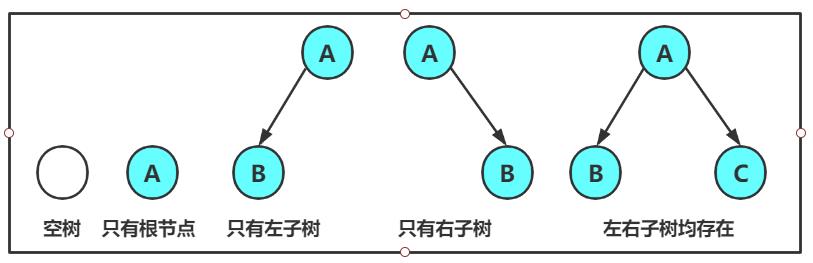
特殊的二叉树：

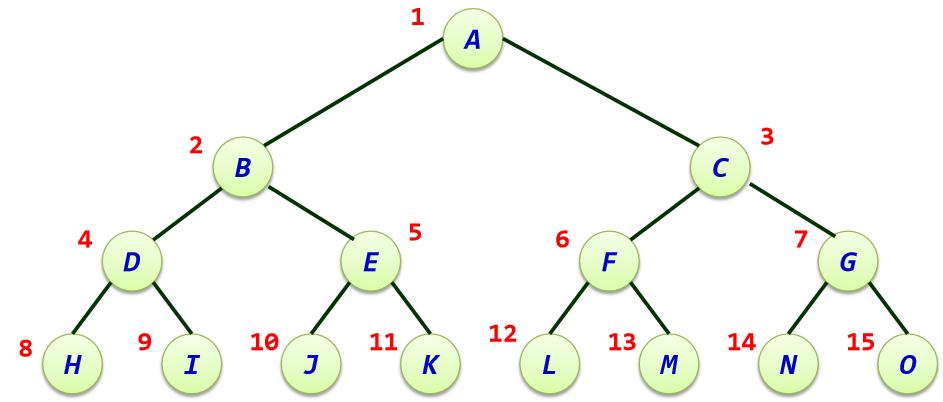
• 1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值2，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为$k$，且结点总数是$2^k-1$，则它就是满二叉树。
• 2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为$k$的，有n个结点的二叉树，当且仅当其每一个结点都与深度为$k$的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树，或者说结点的度为2，最下面一层的叶结点都依次排列在该层最左边的位置上，即完全二叉树。

满二叉树：

完全二叉树：

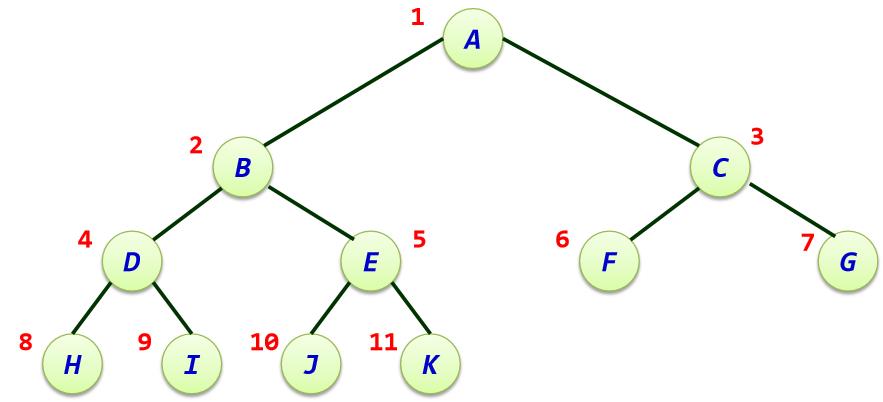
完全二叉树实际上是对应的满二叉树删除叶结点层最右边若干个结点得到的。
问题3：什么是二叉树的深度？
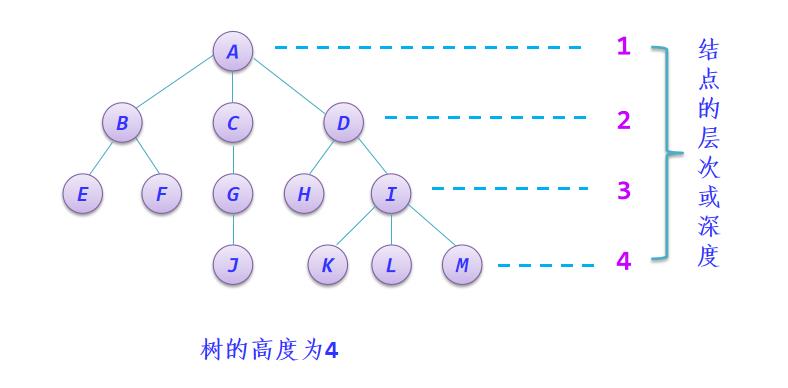
结点的层次和树的高度：树中的每个结点都处在一个层次上。结点的层次从树根开始定义，根结点为第1层，它的孩子结点为第2层，以此类推，一个结点所在的层次为其双亲结点所在的层次加1。

树中结点的最大层次称为树的高度（或树的深度）。

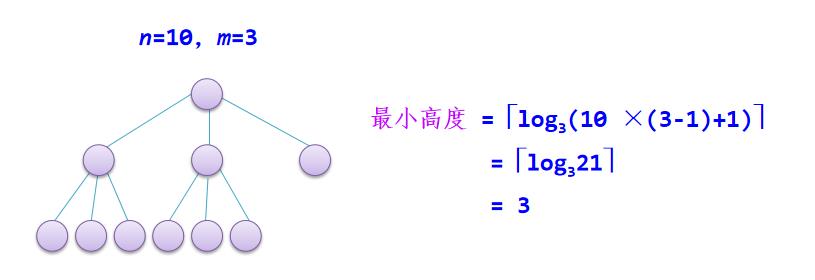
具有n个结点的m次树的最小高度为$lo{g}_m(n(m-1)+1)$。

解题思路：
知道树的概念和二叉树深度概念就可以开始做题了，这道题我们可以采取递归，分别求左子树与右子树的深度，取两者最大值再加上根节点层次就是当前二叉树的最深深度（最高高度）。

递归条件：
$$二叉树结点不为null，为空返回0$$
递归公式：不妨设左子树深度为$highLeft$，右子树深度为$highRight$，则二叉树最深深度为$High$：
$$High=max(highLeft，highRight)+1$$

🔑源代码

Java：

/**
 * Definition for a binary tree node.
 * public class TreeNode 
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x)  val = x; 
 * 
 */
class Solution 
    public int maxDepth(TreeNode root) 
        if (root == null) 
            return 0;
        
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    

C:

/**
 * Definition for a binary tree node.
 * struct TreeNode 
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * ;
 */
int max(int a, int b)

    return a > b ? a : b;


int maxDepth(struct TreeNode* root)
    if(root == NULL) 
    
        return 0;
    
    return 1 + max(maxDepth(root->left), maxDepth(root->right));

C++:

/**
 * Definition for a binary tree node.
 * struct TreeNode 
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) 
 * ;
 */
class Solution 
public:
    int maxDepth(TreeNode* root) 
        if (root == NULL) 
        
            return 0;
        
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    
;

🌱总结

采取递归，分别求左子树与右子树的深度，取两者最大值再加上根节点层次就是当前二叉树的最深深度（最高高度）。
类似题如下：
二叉树的最大深度

---

觉得文章写得不错的老铁们，点赞评论关注走一波！谢谢啦！