ElGamal加密算法｜公钥密码｜数字签名｜密码学｜信息安全

Posted 2022-01-08 Chelse.

ElGamal签名算法

密钥产生

• 确定一个大素数p
• 取p的一个本原根g
• 在Z_p域上选择一个随机数x
• y = g^x%p
• (y, g, p)为公钥，x为私钥

签名算法

设待签名的消息为m

• C₁=g^k%p
• C₂=(H(m)-x*C_1) * k^-1%(p-1)
• 输出签名(C₁,C₂)和消息m

验证算法

• $y^{C_1}\ast C_1^{C_2}=H(m)$

正确性证明

ElGamal加密算法

简单介绍

• EIGamal密码是除了RSA密码之外最有代表性的公开密钥密码

• EIGamal是建立在离散对数的困难问题上的一种公钥体制密码

密钥产生

• 选一个素数p，以及小于p的两个随机数g和x
• 计算 $y=g^x$%p
• 公钥为(y, g, p)，私钥为x

算法加密过程

M为明文

• 选取一个与p-1互素的整数k
• $C_1=g^k$%p
• $C_2=y^{k}M$%p
• $(C_1,C_2)$即为密文

算法解密过程

解密方法：$\frac{C_2}{C_1^x}$%p

证明：

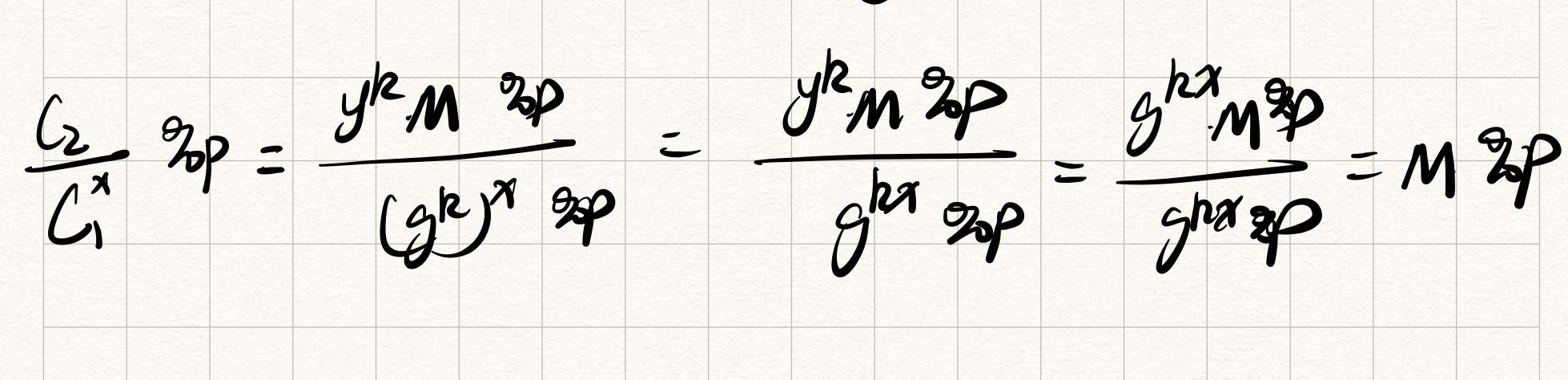
EIGamal 密码体制安全性

由于私钥x是通信双方共享的，别人不知道

所以，当加密完了以后的密文(y, g, p)被别人盗取后，想获取明文M,只能通过 $C_2=y^{k}M$%p来获得，这里面只有k和M是不知道的，所以只要获得了k就能获得M，而想获得k，只有通过 $C_1=g^k$%p来获取，这里面虽然只有k是未知数，但是求离散对数的过程是很困难的，尤其是对p很大的情，所以EIGamal密码体制很安全

举个例子

• 取p=11, g=5, x=2
• 则 y = g ^x%p = 3
• 取 k 为 7， m为10
• 则C₁ = g^k%p = 3
• C₂ = y^k*m % p = 2
• 则C₁^x%p= 9
• 9在模11下的逆元为5
• 所以 $\frac{C_2}{C_1^x}=2\ast 5$%10 =10，所以解密成功

ElGamal签名算法

密钥产生

• 确定一个大素数p
• 取p的一个本原根g
• 在Z_p域上选择一个随机数x
• y = g^x%p
• (y, g, p)为公钥，x为私钥

签名算法

设待签名的消息为m

• 取一个与p-1互质的k

• C₁=g^k%p

• C₂=(H(m)-x*C₁) * k^-1%(p-1)

• 输出签名(C₁,C₂)和消息m

验证算法

• $y^{C_1}\ast C_1^{C_2}=g^{H(m)}$%p

正确性证明

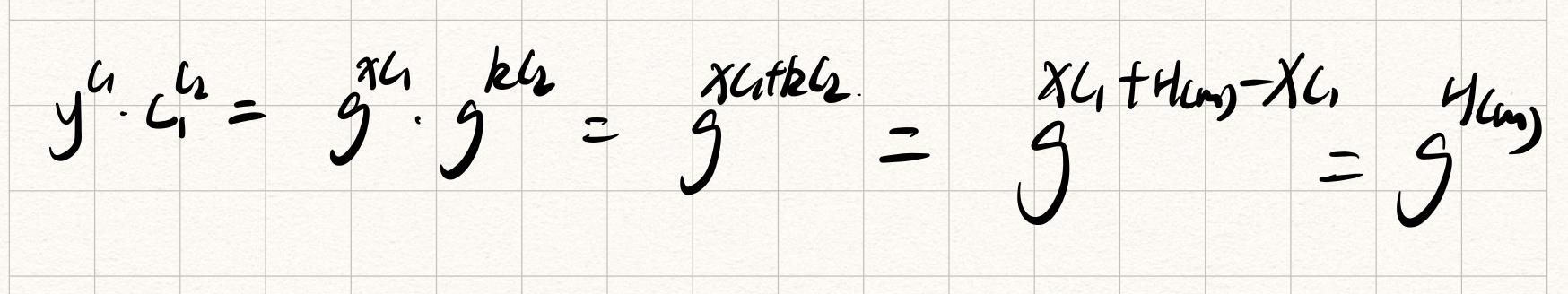
举个例子

• p = 11
• g = 2,(注意必须取p的一个生成元)
• x = 6
• 计算y = g^x%p = 9
• 取 k = 7
• 计算C₁=g^k%p = 7
• 利用扩展欧几里得计算k在模p-1意义下的逆元k^-1= 3
• 假设需要验证的消息m经过哈希后的结果是H = 10
• 则计算C₂ = ((H - x * C1) * k_-1 ) % (p-1) = 4
• 验证：计算$y^{C_1}\ast C_1^{C_2}$%p = 1
• 计算H^g%p=1
• 所以验证成功