Python(离散数学实验)求不超过4个命题变元任意公式的主合取范式主析取范式真值表和成真赋值
Posted kibety
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python(离散数学实验)求不超过4个命题变元任意公式的主合取范式主析取范式真值表和成真赋值相关的知识,希望对你有一定的参考价值。
在上离散数学课程时,老师给了这么一个问题:
1. 对给出的任意一个命题公式(不超过四个命题变元),使学生会利用编程软件表示出来,并且能够计算它在各组真值指派下所应有的真值,画出其真值表。
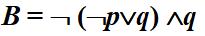 的真值表;
的真值表;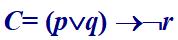 的真值表;
的真值表;
2. 编程解决下列问题:
求公式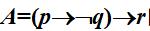 的主析取范式与主合取范式,并求公式的成真赋值和成假赋值。
的主析取范式与主合取范式,并求公式的成真赋值和成假赋值。
这对于是个菜狗的我简直是降维打击,但是认认真真的学习完相关过程后还是觉得很有趣的。下面我总结一下我个人的学习过程:
1.首先要搞懂什么是主析取范式和主合取范式,成真赋值等一系列概念。
2.了解了概念后要找出实验的突破口:求真值表,只要搞定了真值表,其他的都能够水到渠成。
3.要解决计算的问题:对于一般带有符号和括号的运算,我们一般将算式转化为逆波兰表达式的顺序进行一些列运算。
什么是逆波兰排序?
看完这两个视频,三分钟搞定:
逆波兰 - 上(中缀表达式 转 后缀表达式)_哔哩哔哩_bilibili
逆波兰 - 下(后缀表达式计算结果)_哔哩哔哩_bilibili
在转化的过程中会遇到一系列的问题,例如在离散数学里有一个按位运算符“㇕(非)”,这处理起来很麻烦。稍后我会在文章中给出解决办法。
4.要有简洁大方的输入输出界面,这里将用到python里的easygui的库来设计一个简易的gui界面
pip install easygui下面直接上代码
1) 提示用户输入公式并获取命题变元的数量
import easygui as eg
def GetGongshi(): # 通过简易Gui让用户输入命题变元个数和公式
eg.textbox(msg="您可以选择复制下列标准逻辑运算符号进行输入:",text="非:﹁\\n合:∧\\n析取:∨\\n蕴含:→\\n等价:↔\\n为了保证识别正确请按照标准符号格式输入")
msg="请输入命题变元的数量(1-4):"
while 1:
num = eg.enterbox(msg,title="求命题公式的真值表")
if num == "1":
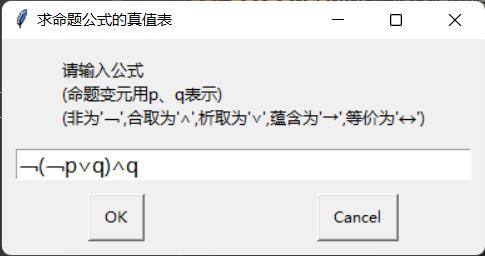
Gongshi=eg.enterbox(msg="请输入公式\\n(命题变元用p表示)\\n(非为'﹁',合取为'∧',析取为'∨',蕴含为'→',等价为'↔')",title="求命题公式的真值表")
break
elif num == "2":
Gongshi = eg.enterbox(msg="请输入公式\\n(命题变元用p、q表示)\\n(非为'﹁',合取为'∧',析取为'∨',蕴含为'→',等价为'↔')", title="求命题公式的真值表")
break
elif num == "3":
Gongshi = eg.enterbox(msg="请输入公式\\n(命题变元用p、q、r表示)\\n(非为'﹁',合取为'∧',析取为'∨',蕴含为'→',等价为'↔')", title="求命题公式的真值表")
break
elif num == "4":
Gongshi = eg.enterbox(msg="请输入公式\\n(命题变元用p、q、r、s表示)\\n(非为'﹁',合取为'∧',析取为'∨',蕴含为'→',等价为'↔')", title="求命题公式的真值表")
break
else:
msg = "输入有误请重新输入\\n请输入命题变元的数量(1-4):"
return Gongshi+num这里最后return的是一个字符串,num作为变元个数放在字符串的最后一个元素上
2) 获取由公式转化成得到逆波兰表达式
#获取逆波兰顺序转化后的公式
def GetNiBoLan(Gongshi): #Gongshi必须转为列表才能使用
Fuhao = ["﹁","∨","∧","→","↔","("] #右括号因为作为符号栈的逻辑元素不加入Fuhao标识符
Yuansu = ["p","q","r","s"]
FuhaoZhan = [] #符号栈
NiBoLan = [] #逆波兰表达式的公式(后缀表达式)
GS_pop = "" #公式栈的出栈元素
FH_pop = "" #符号栈的出栈元素
while len(Gongshi)!=0: #这里会遇到一系列问题
GS_pop = Gongshi.pop(0)
if GS_pop in Fuhao:
if len(FuhaoZhan) != 0: #在处理符号栈里"﹁"时为了保证逻辑上的正确我们一般处理的原则是遇到"("不pop遇到其他的pop
if FuhaoZhan[-1] == "﹁" and GS_pop!="(": #当遇到运算符时我们的"﹁"就先从栈里pop到表达式里去
NiBoLan.append(FuhaoZhan.pop())
FuhaoZhan.append(GS_pop)
elif GS_pop in Yuansu:
NiBoLan.append(GS_pop)
if len(FuhaoZhan) != 0:
if FuhaoZhan[-1] == "﹁": #当遇到元素时我们的"﹁"先让元素进入表达式后再进入
NiBoLan.append(FuhaoZhan.pop())
elif GS_pop == ")":
FH_pop = FuhaoZhan.pop()
while FH_pop != "(":
NiBoLan.append(FH_pop)
FH_pop = FuhaoZhan.pop()
while len(FuhaoZhan) != 0: #符号栈里剩下的都pop出来就完事了
FH_pop = FuhaoZhan.pop()
NiBoLan.append(FH_pop)
return NiBoLan这里咱们要解决逆波兰在加减乘除运算中不会出现的按位运算符的问题:
例如给出公式:
﹁p∧q 如果按照一般的逆波兰表示法将转化为 pq∧﹁ 这相当于﹁(p∧q) ,这显然是错误的,所以为了解决这一问题,我们采用一种针对逻辑运算符“﹁”的原则:
在符号栈里:如果“﹁”后面下一个入栈的不是“("我们就让“﹁”提前出符号栈
在表达式里:如果“﹁”后面下一个入栈的是元素(p,q,r,s),我们先让元素进入表达式“﹁”随后进入
这样就保证了最后的运算逻辑正确,按照这一原则,公式正确的表达示为p﹁q∧
3) 根据逻辑运算符的运算规则编写一个运算器函数
#各符号的逻辑运算
def JiSuan(*CanShu): #这里使用了收集参数,因为参数个可能为一个或者两个:
# 下面分别是析取、合取、蕴含、等价的逻辑运算
if CanShu[0] == "∨":
if CanShu[1] == 1 or CanShu[2] == 1:
return 1
else:
return 0
if CanShu[0] == "∧":
if CanShu[1] == 0 or CanShu[2] == 0:
return 0
else:
return 1
if CanShu[0] == "→":
if CanShu[1] == 1 and CanShu[2] == 0:
return 0
else:
return 1
if CanShu[0] == "↔":
if CanShu[1] != CanShu[2]:
return 0
else:
return 1
if CanShu[0] == "﹁":
if CanShu[1] == 1:
return 0
else:
return 14) 计算并获取真值表
#获得真值表
def GetValue(NiBoLan,num): # num为命题变元个数
NiBoLanList=NiBoLan.copy() #这个列表用来存储逆波兰表达式,方便多次输出
Fuhao = [ "∨", "∧", "→", "↔"] #逆波兰表达式把括号去掉了,"﹁"作为特殊位运算做特例处理
Yuansu = ["p", "q", "r", "s"]
YuansuZhan = []
YS_value = "p":0,"q":0,"r":0,"s":0,"k":0 #这里用字典来匹配变元字符的逻辑值,k为计算过程中的临时变量,默认值都为0
NBL_pop = ""
Value = [] #这个用来存储所有赋值情况下公式的真值(按赋值顺序存储就行)
YS_valuelist = []#储存真值赋值
count = 0 #这个用来控制循环
YS_temp=""
while count < 2**num:
NiBoLanList = NiBoLan.copy() #每次循环重置逆波兰列表值循环利用,注意不能直接用等于,等于是引用在pop引用变量时被引用变量也会被pop
YS_value = "p": 0, "q": 0, "r": 0, "s": 0, "k": 0 #同理字典也重置
YS_temp = bin(count)[2:] #十进制转二进制
YS_temp = [int(each) for each in YS_temp] #二进制字符串转列表
YS_temp.reverse()
while len(YS_temp) < num: #长度小于num时其他位赋值0
YS_temp.append(0)
YS_temp.reverse()
YS_valuelist.append(YS_temp[:])
while len(YS_temp) < 4:
YS_temp.append(0) #保证标准的输出格数pqrs
YS_value["p"] = YS_temp[0] #这样这样pqrs四位数的二进制数就赋值好了
YS_value["q"] = YS_temp[1]
YS_value["r"] = YS_temp[2]
YS_value["s"] = YS_temp[3]
while len(NiBoLanList) != 0:
NBL_pop=NiBoLanList.pop(0)
if NBL_pop in Yuansu:
YuansuZhan.append(NBL_pop)
elif NBL_pop in Fuhao:
YS_value["k"] = JiSuan(NBL_pop,YS_value[YuansuZhan.pop(-2)],YS_value[YuansuZhan.pop()]) #只要不是否定,从元素栈顶pop变元出来用字典转换后进行逻辑计算
YuansuZhan.append("k")
elif NBL_pop == "﹁":
YS_value["k"] = JiSuan(NBL_pop, YS_value[YuansuZhan.pop()])
YuansuZhan.append("k")
Value.append(YS_value[YuansuZhan.pop(0)])
count += 1
YS_valuelist.append(Value) #将真值表和公式真值绑定一起到时候pop分开就行
return YS_valuelist在计算时也要注意“﹁”是单个元素的运算符哦
最后的 YS_valuelist是所有真值赋值和公式真值的二维数组例如﹁p∧q返回的是:
[[0, 0], [0, 1], [1, 0], [1, 1], [0, 1, 0, 0]]
5) 打印真值表、主析取范式、主合取范式、成真赋值
#打印真值表,主析取范式,主合取范式与成真赋值
def FormPrint(YS_valuelist, num):
value=YS_valuelist.pop() #将公式真值与真值表分开
msg="公式0真值表结果如下:\\n".format(GongShiChar)
YuansuList=["p","q","r","s"]
#输出真值表
for i in range(num):
msg = msg+" "+YuansuList[i]+" "
msg = msg+" 真值\\n"
for i in range(len(YS_valuelist)):
for each in YS_valuelist[i]:
msg = msg+" "+str(each)+" "
msg = msg+" "+str(value[i])+" \\n"
#输出主析取范式
msg = msg+"主析取范式为:"
for each in YS_valuelist:
if value[YS_valuelist.index(each)] == 1:
msg = msg+"("
for i in range(len(each)):
if each[i] == 1:
msg = msg+YuansuList[i]
else:
msg = msg+"﹁"+YuansuList[i]
if i != len(each)-1:
msg = msg+"∧"
msg = msg+")"
if 1 in value[YS_valuelist.index(each)+1:]:
msg = msg+"∨"
#输出主合取范式
msg = msg +"\\n主合取范式为:"
for each in YS_valuelist:
if value[YS_valuelist.index(each)] == 0:
msg = msg+"("
for i in range(len(each)):
if each[i] == 0:
msg = msg+YuansuList[i]
else:
msg = msg+"﹁"+YuansuList[i]
if i != len(each)-1:
msg = msg+"∨"
msg = msg+")"
if 0 in value[YS_valuelist.index(each)+1:]:
msg = msg+"∧"
#输出成真赋值
msg = msg+"\\n成真赋值为:\\n"
for i in range(len(value)):
if 1 not in value:
msg = msg +"该式为永假式"
break
if 0 not in value:
msg = msg + "该式为永真式"
break
if value[i] == 1:
msg = msg +" "+str(YS_valuelist[i])+"\\n"
eg.msgbox(msg,title="输出结果")6) 主函数部分
#主函数部分
GongShi_And_num = GetGongshi()
GongShi = [each for each in GongShi_And_num]#字符串列表化
num = int(GongShi.pop()) #最后一个元素存放的变元数量信息,pop出来转化为int就行
GongShiChar=GongShi_And_num[:-1] #用来存放公式字符串,供以后输出
NiBoLan = GetNiBoLan(GongShi) #公式转逆波兰表达式
YS_valuelist = GetValue(NiBoLan,num) #逆波兰表达式求真值
FormPrint(YS_valuelist,num) #输出数据测试结果如下:
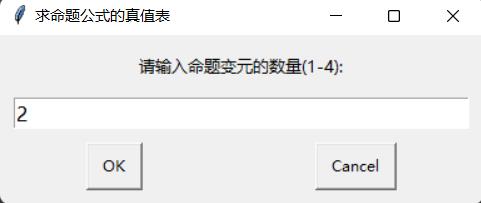
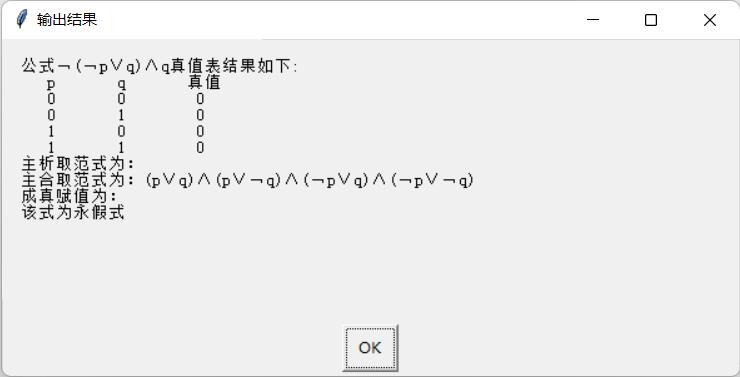
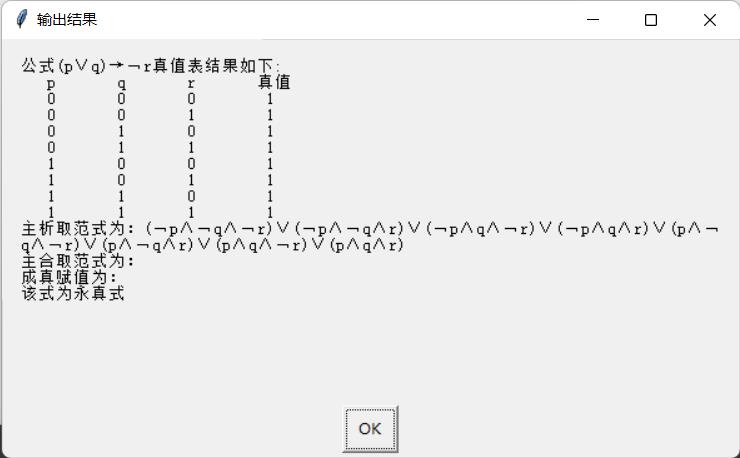
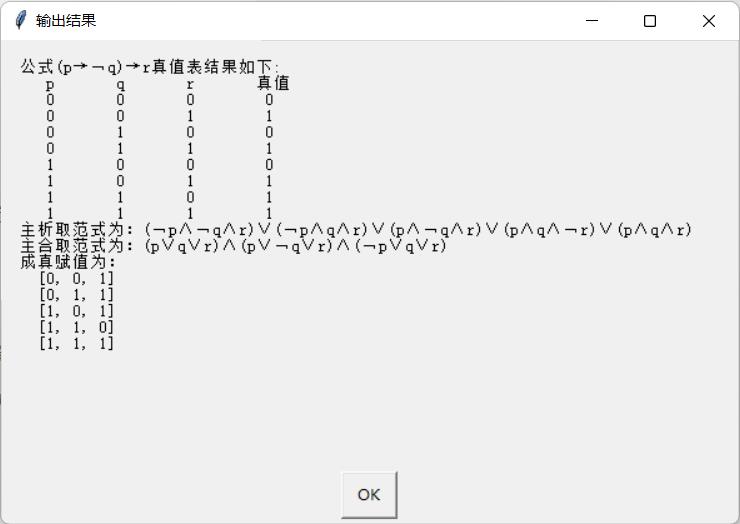 如果代码出现错误或异常,欢迎私信!
如果代码出现错误或异常,欢迎私信!
完整代码:GitHub - Kibety/-: 求主合取范式、主析取范式、成真赋值、真值表 https://github.com/Kibety/-/tree/main
https://github.com/Kibety/-/tree/main
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
以上是关于Python(离散数学实验)求不超过4个命题变元任意公式的主合取范式主析取范式真值表和成真赋值的主要内容,如果未能解决你的问题,请参考以下文章