每天一道算法题（java数据结构与算法)——＞链表中环的入口节点

Posted 2022-01-08 stormzhuo

这是LeetCode上的 [022，链表中环的入口节点]，难度为 [中等]

题目
给定一个链表，返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环，则返回 null。

思路分析

第一步：确定链表是否存在环

定义两个指针（快慢指针）指向头节点，然后遍历链表，快指针每次移动2步，慢指针每次移动1步，如果存在环，则它们一定会相遇（可以想象环为一个环形跑道，跑得快得人一定会和慢得人相遇）

第二步：在有环得链表中找到入口节点

有两种方式，一种是需要知道环中节点数目，另一种是不需要知道环中节点数目，这样就会有两种题解

题解1：（需要知道环中节点数目的解法）

求环中节点数目求法得步骤

1. 利用第一步的快慢指针找到环中的一个节点（相遇节点）
2. 从这个节点（相遇节点）开始遍历链表并计数，当再次回到这个节点时就可以得到环中节点的数目count

求有环链表入口节点步骤

1. 定义两个指针p1,p2指向头节点
2. 第1个指针从链表的头节点开始遍历count步，第2个指针p2保持不动；
3. 从第count步开始指针p2也从链表的头结点开始和指针p1以相同的速度遍历。
4. 当指针p1和p2相遇时，相遇的节点即为入口节点

题解2：（不需要知道环中节点数目的解法）

求有环链表入口节点步骤

1. 利用第一步的快慢指针找到环中的一个节点（相遇节点）
2. 定义一个指针指向头节点，让它和相遇节点以相同的速度遍历。
3. 当两个节点相遇时，相遇的节点即为入口节点

题解1代码实现（需要知道环中节点数目的解法）
解类如下，类中包含静态两个方法，一个是获取链表环中相遇结点（不存在环返回null)的方法，另一个是求链表环入口结点的方法

public class Solution 

    public static ListNode getNodeInLoop(ListNode head) 
        // 定义两个结点（快慢指针），初始化为头结点
        ListNode slow = head;
        ListNode fast = head;
       /* 遍历链表，slow每次移动1步，fast每次移动2步
          循环条件为fast不为null且fast下一个结点也不为null
          防止fast.next和fast.next.next报空指针异常*/
        while (fast != null && fast.next != null) 
            slow = slow.next;
            fast = fast.next.next;
            // 当fast=slow时即两个结点相遇，返回相遇结点
            if (fast == slow) 
                return fast;
            
        
        return null;
    

    public static ListNode detectCircle1(ListNode head) 
        // 获取链表环的相遇结点
        ListNode nodeInLoop = getNodeInLoop(head);
        // 若为null则链表不存在环
        if (nodeInLoop == null) 
            return null;
        
        // 记录环的个数，初始为1
        int count = 1;
        // 定义一个新结点，初始为相遇结点
        ListNode n = nodeInLoop;
        /*累加count，循环终止条件为n的下一结点为相遇结点
          故此count会比环数目少一个，则count必须初始为1*/
        while (n.next != nodeInLoop) 
            count++;
            n = n.next;
        
        // 定义一个新结点front，初始为头结点
        ListNode front = head;
        // front先遍历count步
        for (int i = 0; i < count; i++) 
            front = front.next;
        
        // 定义一个新结点back，初始为头结点
        ListNode back = head;
        /* front,back以相同的速度遍历，front从count步开始，back从头结点开始
        当back=front时，两个结点相遇，终止循环，相遇结点即为环入口结点*/
        while (back != front) 
            back = back.next;
            front = front.next;
        
        return back;
    

结点类

public class ListNode<T> 

    T val;
    ListNode next;

    public ListNode() 

    

    public ListNode(T val) 
        this.val = val;
    

    public ListNode(T val, ListNode next) 
        this.next = next;
    

测试用例1

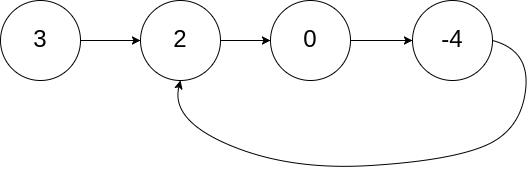
环入口结点第二结点，值为2

测试用例2

环入口结点第一结点，值为1

测试代码

public class Test 

    @org.junit.Test
    public void test1() 
        ListNode<Integer> head = new ListNode<>(3);
        ListNode<Integer> listNode = new ListNode<>(2);
        ListNode<Integer> listNode1 = new ListNode<>(0);
        ListNode<Integer> listNode2 = new ListNode<>(-4);
        head.next = listNode;
        listNode.next = listNode1;
        listNode1.next = listNode2;
        listNode2.next = listNode;
        ListNode n = Solution.detectCircle1(head);
        System.out.println("入口结点的值:" + n.val);
    

    @org.junit.Test
    public void test2() 
        ListNode<Integer> head = new ListNode<>(1);
        ListNode<Integer> listNode = new ListNode<>(2);
        head.next = listNode;
        listNode.next = head;
        ListNode n = Solution.detectCircle2(head);
        System.out.println("入口结点的值:" + n.val);
    

复杂度分析

假设链表长度为n
时间复杂度：在最初找相遇结点时，结点走过得长度不会超过链表长度（可以理解为循环的次数不会超过链表长度），故O(n)。同理在求环入结点数，以及求环入口也为O(n)，则总时间复杂度为O(n) + O(n) + O(n) = O(n)
空间复杂度：只声明了几个固定的结点，故空间复杂度为O(1)

题解2代码实现（不需要知道环中节点数目的解法）

public class Solution 

    public static ListNode detectCircle2(ListNode head) 
        // 获取链表环的相遇结点
        ListNode nodeInLoop = getNodeInLoop(head);
        // 若为null则链表不存在环
        if (nodeInLoop == null) 
            return null;
        
        // 定义一个新结点n，初始为头结点
        ListNode n = head;
       /* n和相遇结点以相同的速度遍历
       当n = nodeInLoop时，两结点相遇，循环终结，相遇结点即为链表环的入口*/
        while (n != nodeInLoop) 
            n = n.next;
            nodeInLoop = nodeInLoop.next;
        
        return n;
    

复杂度分析
假设链表长度为n
时间复杂度：在最初找相遇结点时，结点走过得长度不会超过链表长度（可以理解为循环的次数不会超过链表长度），故O(n)。同理在求环入口也为O(n)，则总时间复杂度为O(n) + O(n) = O(n)
空间复杂度：只声明了几个固定的结点，故空间复杂度为O(1)