学习深度网络需要直观的感知

Posted 2022-01-08 卓晴

简 介： 对于人工智能以及相关的领域学习，一个重要的经验就是能够通过实际动手编程和对实际数据进行处理，才能够很好的理解深度学习背后的数学原理以及该工具的性能。还是让我们把“纸上得来终觉浅,绝知此事要躬行”这句话始终记在心头吧。

关键词： 深度学习，可视化，CNN

 

§01 背景介绍

---

  这是一篇在Github上 SkalskiP 写的一篇博文，介绍他深度学习的一些体会 ，原文可以在下面链接看到。

• ILearnDeepLearning.py : https://github.com/SkalskiP/ILearnDeepLearning.py

  下面是对原文的介绍。

1.1 前言

  俗话说，纸上得来终觉浅,绝知此事要躬行（Nothing develops and teaches you like getting your hands dirty。）这个Github仓库中包含了一些与深度学习、数据科学相关的小程序，大部分与在 Medium 中发布的文章有关系，主要是对其中文章进行说明和补充。对我来说，习惯于将自己的学习的过程记录下来，也可以帮助其他人理解人工神经网络相关问题。我希望这个Github仓库的内容被人们发现是有趣和有用的。建议你在阅读这些文章同时也动手体验给出的代码的效果。

▲ 图1.1.1 ILearningDeepLearning.py

1.1.1 建立运行环境

# clone repository
git clone https://github.com/SkalskiP/ILearnDeepLearning.py.git

# navigate to main directory
cd ILearnDeepLearning.py

# set up and activate python environment
apt-get install python3-venv
python3 -m venv .env
source .env/bin/activate

# install all required packages
pip install -r requirements.txt

评论： 通过他这篇博文，可以看到作者 SkalSkiP不仅仅是一个研究人员，更适合做一个教学老师。

 

§02 动图展示

---

2.1 几篇博文中的动图

2.1.1 深度学习中的数学原理

  如果你对于深度学习背后的机理感兴趣，可以看看这篇博文： Deep Dive into Math Behind Deep Networks 。文中将于学习过程中的梯度下降、激活函数以及分类边界进行了视觉化展示。通过这些精美的动图可以对文章中讲述的问题进行很好的补充。下面展示一些可视化的动图。

▲ 图2.1.1 在Keras模型中每次迭代之后对应的分类器的分类边界，将这些边界变化合成一个动图

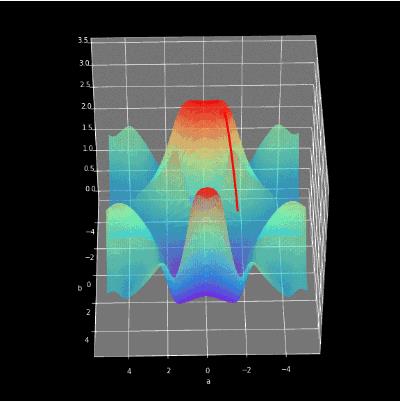
▲ 图2.1.2 将梯度下降进行可视化

2.1.2 使用NumPy进行可视化

  在 Let’s code a Neural Network in plain NumPy 中介绍了人工神经网络理论之后，展示了如何使用NumPy工具来实现神经网络实际工作模型。在Notebook文件中包含了一些代码，是对Keras平台建立的网络模型的NumPy完整的实现代码，文中大量的注释也可以让你对相关文章中网络功能实现有着清晰的理解。

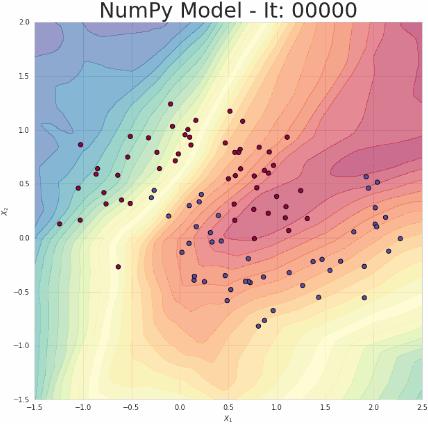
▲ 图2.2.1 使用简单的NumPy编写的分类模型的分类边界演化动图

2.1.3 防止网络过学习

  Preventing Deep Neural Network from Overfitting 文中 阐述了网络训练过程中的过学习（Overfit）现象以及预防的方法。作者对不同的正则化阐述进行了仿真，分析了对权系数矩阵的影响。文中给出结果的可视化动图。

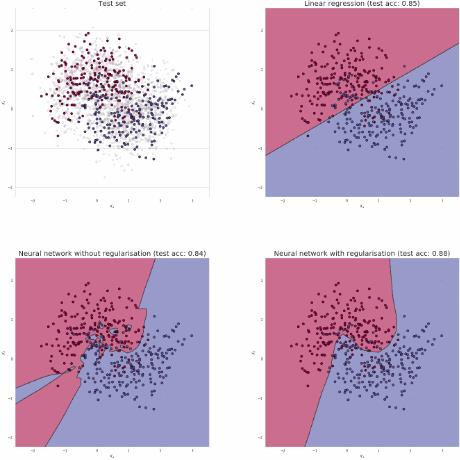
▲ 图2.1.4 使用线性回归、人工神经网络以及带有正则化条件的神经网络创建的分类边界
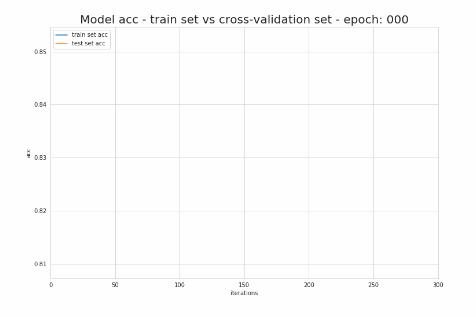
▲ 图2.1.5 神经网络训练过程中的训练精度和验证精度的变化曲线

2.1.4 如何利用优化其加速网络训练？

  作者的这篇文章中 How to train Neural Network faster with optimizers? 介绍了作者纯粹使用Numpy来建立自己的人工神经网络，这当然是一个有挑战性的工作，但使得作者对神经网络背后的工作机制有了更深入和广泛的理解。这使得他对于影响网络性能的很多参数的作用有了更充分的理解，比如如何进行网络结构选择、调整训练超参、正确的网络的初始化等等。对于影响网络学习速度的关键因素-选择合理的优化策略，是本文的重点。

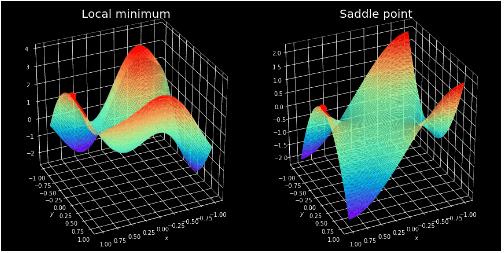
▲ 图2.1.6 展示初始化位置是如何影响网络训练的
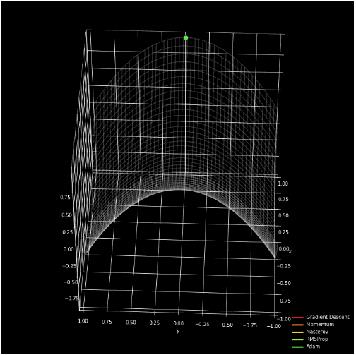
▲ 图2.1.7 不同优化器的效果对比

2.1.5 创建动图的简单方法

  Simple Method of Creating Animated Graphs 给出了作者在自己的文章和工程中是如何制作这些有趣的动图方法，这使得他可以更有效的表达自己的思想。文中介绍了利用MatPlitLib制作动图的简单方法。

▲ 图2.1.8 使用Matplotlib中的API制作的Lorenz混沌吸引子动图

2.2 卷积神经网络中数学原理

  在 Gentle Dive into Math Behind Convolutional Neural Networks 中作者讨论了卷积神经网络相关的理论问题，这也是对一个小的工程项目的准备。作者计划使用卷积神经网络创建自己的简易实现版本。因此，文中的动图主要集中在选择滤波器进行卷积的过程。

  下面是图像卷积的数学表达式：

$$G\left[m,n\right]=\left(f\ast h\right)\left[m,n\right]=\sum _j\sum _{k}h\left[j,k\right]f\left[m-j,n-k\right]$$

  对应的像素操作可以使用如下动图表示：

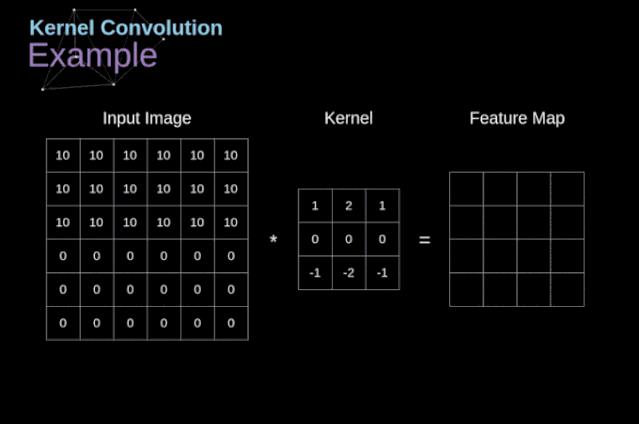
▲ 图2.2.1 卷积核的例子

  位于图像不同位置（中心、边缘、角落）是如何影响卷积结果的。从而产生了有效卷积和“相同卷积”的概念。

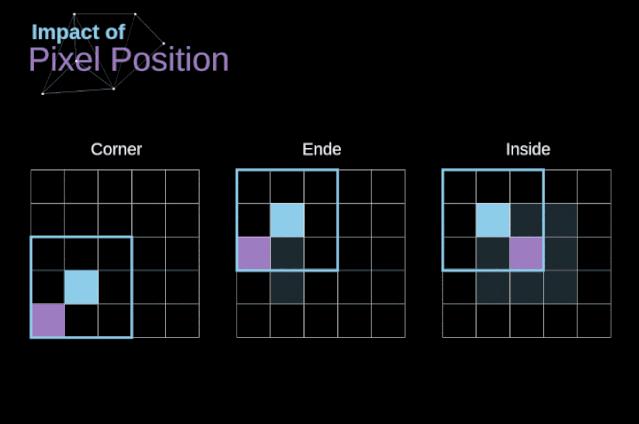
▲ 图2.2.2 像素位置如何影响卷积结果的

  不同的卷积移动步幅（Stride） 会影响结果的大小。

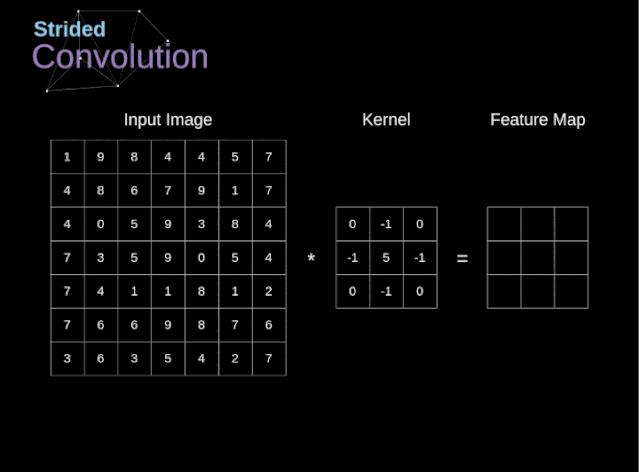
▲ 图2.2.3 卷积步幅对于结果尺寸的影响

  为了使得输出结果边长与输入相同，则需要在数据边缘填充一定的数据。

$$p=\frac{f-1}{2}$$

公式中：

p：填充宽度
f：卷积核尺寸

  如果已知输入尺寸（$n_{in}$）、填充宽度（$p$）、卷积核尺寸（$f$）以及移动步幅（$s$），那么输出图像的边长为：

$$n_{out}=\left[\frac{n_{in}+2p-f}{s}+1\right]$$

  文中作者还讨论了卷积从二维到三维转换，以及卷积是如何实现参数共享的过程。

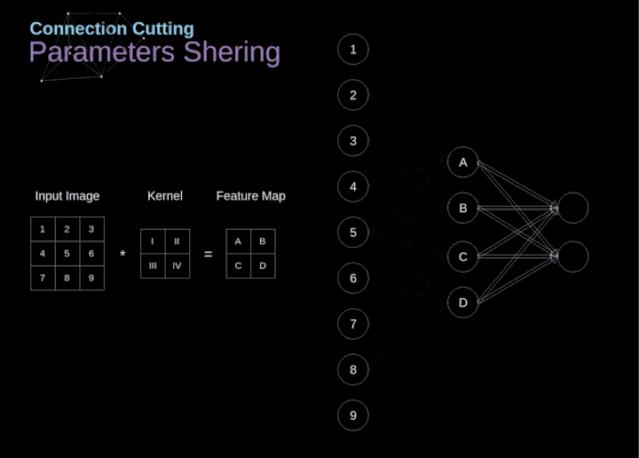
▲ 图2.2.4 连接裁剪和参数共享

  对于卷积运算的误差反向传播过程一直是所有人工神经网络教学中的难点。借助于“全卷积矩阵”的概念，可以将卷积反向误差传播过程也等效成一个卷积过程。

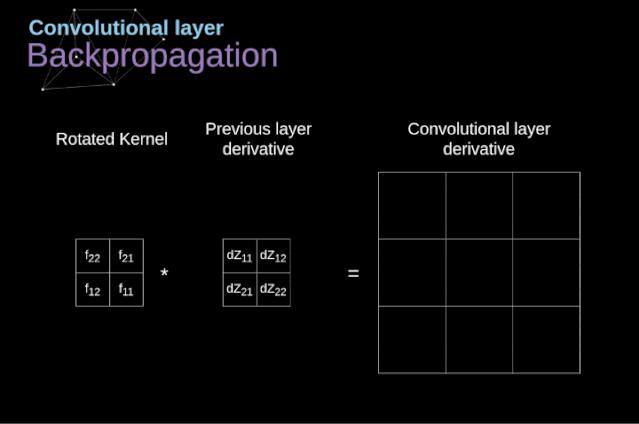
▲ 图2.2.5 卷积的反向传播过程
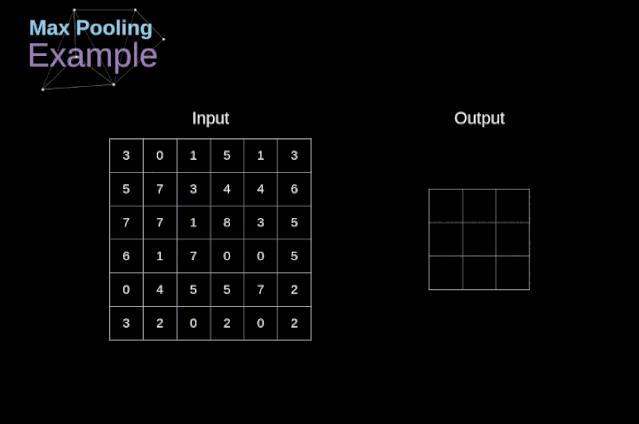
▲ 图2.2.6 MaxPooling 过程

  利用掩码技术可以实现对MaxPooling过程的反向梯度传播。

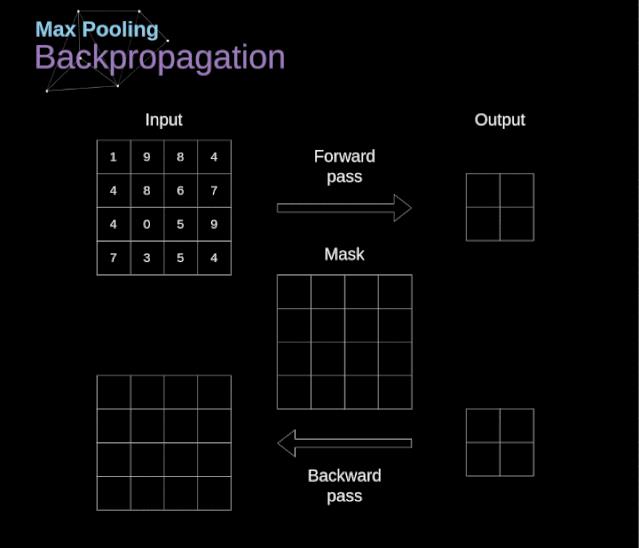
▲ 图2.2.7 对于MaxPooling层中的反向传播过程的展示

 

※ 总  结 ※

---

  对于人工智能以及相关的领域学习，一个重要的经验就是能够通过实际动手编程和对实际数据进行处理，才能够很好的理解深度学习背后的数学原理以及该工具的性能。还是让我们把“纸上得来终觉浅,绝知此事要躬行”这句话始终记在心头吧。

▲ 图3.1 今年信标灯的触发无需再使用磁铁触发

---

■ 相关文献链接:

• SkalskiP 写的一篇博文，介绍他深度学习的一些体会
• Medium
• Deep Dive into Math Behind Deep Networks
• Let’s code a Neural Network in plain NumPy
• Preventing Deep Neural Network from Overfitting
• How to train Neural Network faster with optimizers?
• Simple Method of Creating Animated Graphs
• Gentle Dive into Math Behind Convolutional Neural Networks

● 相关图表链接:

• 图1.1.1 ILearningDeepLearning.py
• 图2.1.1 在Keras模型中每次迭代之后对应的分类器的分类边界，将这些边界变化合成一个动图
• 图2.1.2 将梯度下降进行可视化
• 图2.2.1 使用简单的NumPy编写的分类模型的分类边界演化动图
• 图2.1.4 使用线性回归、人工神经网络以及带有正则化条件的神经网络创建的分类边界
• 图2.1.5 神经网络训练过程中的训练精度和验证精度的变化曲线
• 图2.1.6 展示初始化位置是如何影响网络训练的
• 图2.1.7 不同优化器的效果对比
• 图2.1.8 使用Matplotlib中的API制作的Lorenz混沌吸引子动图
• 图2.2.1 卷积核的例子
• 图2.2.2 像素位置如何影响卷积结果的
• 图2.2.3 卷积步幅对于结果尺寸的影响
• 图2.2.4 连接裁剪和参数共享
• 图2.2.5 卷积的反向传播过程
• 图2.2.6 MaxPooling 过程
• 图2.2.7 对于MaxPooling层中的反向传播过程的展示
• 图3.1 今年信标灯的触发无需再使用磁铁触发