Java版算法思想贪心算法&动态规划

Posted 2022-01-08 chenry777

本文涉及到的贪心和动态规划代码都已上传github可自取，解释不明之处可评论留言，能力范围内一定尽力解答: github https://github.com/chenruoyu0319/data-structure-for-java/tree/main/%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95%26%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92

一、贪心算法

概念：贪心算法又叫做贪婪算法，它在求解某个问题是，总是做出眼前最大利益。

也就是说只顾眼前不顾大局，所以它是局部最优解。核心点：通过局部最优推出全局最优。

思考1：某天早上公司领导找你解决一个问题，明天公司有N个同等级的会议需要使用同一个会议室，现在给你这个N个会议的开始和结束时间，你怎么样安排才能使会议室最大利用？即安排最多场次的会议？

现在我们怎么去贪？也就这个我们选择的贪心策略：、

选时间最短：1-3，2~4,3~5,4~6

按结束时间从小到大排序：首先把第一个加入我们可以开会的列表。之后只要开始时间是大于我们上一个的结束时间的就可以开

咱们来看思考题1：

0点~9点：9点之前开始的会议都不行了。

8点~10点

10点~12点：12点

8点~20点

思路：

按结束时间从小到大排序：首先把第一个加入我们可以开会的列表。之后只要开始时间是大于我们上一个的结束时间的就可以开

贪心算法的套路：一定会有一个排序。哈夫曼编码，贪心算法，压缩算法。最短路径

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

二、贪心算法的总结

贪心算法其最重要的两个点就是：

1.贪心策略：排序

2.通过局部最优解能够得到全局最优解

一般通过以下问题就可以通过贪心算法解决：

1.针对某个问题有限制值，以及有一个期望的最好结果，通常是从某些数据中选出其中一些，达到最好的结果。

2.一般会有一个排序，找出贡献最大的。

3.举例看贪心是否可以解决。

一般用在任务调度，教师排课等系统。

三、动态规划

实际上，用贪心算法解决问题的思路，并不总能给出最优解，比如来看下一个问题：

思考2 经典问题：背包问题

小偷去某商店盗窃，背有一个背包，容量是50kg，现在有以下物品（物品不能切分,且只有一个），请问小偷应该怎么拿才能得到最大的价值？

重量 价值

物品1 10kg 60元 60 / 10 = 6

物品2 20kg 100元 100/20 = 5

物品3 40kg 120元 120/40 = 3

性价比最高：贪心的策略，按性价比排序,得到的最大价值是 60+100=160，背包装了30kg

但很显然最大的价值是：40+10（kg）=120+60=180

如果用贪心可以解决问题吗？

并不能,如果从解决现实种问题的来说，你就按你自己的的想法拿。

我们这边有一个最朴素的思路解决这个问题，就是枚举：

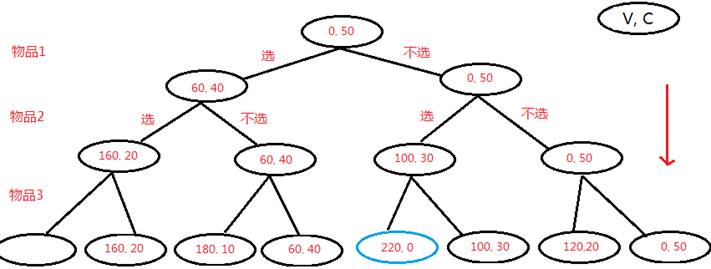
遍历它：每个物品只有2个选择就是拿与不拿吧，我们就用枚举，排列组合；

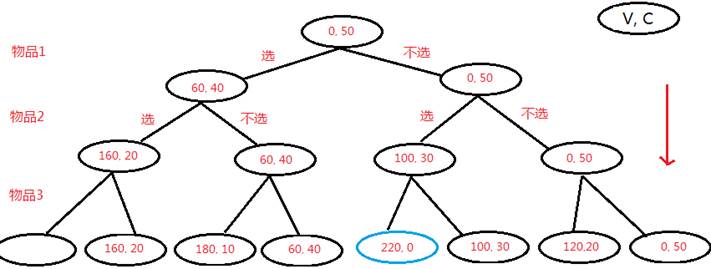
000 111 011 010 001 100 101 110 ，3个物品公有8种组合，如果换成10个物品，20个物品呢？ 其时间复杂度会达到2^n次，显然是我们所不能接受的，不光我们不能接受，程序也不能接受，他告诉我他算不出来

于是前人们设计出了一种思路来优化这种计算，就是动态规划。

比如举个同样的栗子，这边我们有个，5kg的袋子，可以选择装的物品有Kg：1 2 4，钱：6 10 12。

我们把5kg的袋子，拆分成1kg，1kg这样子计算，里面的表格就表示当前重量下能装的最多的钱。表格的数列就表示是要装的物品

	1kg	2kg	3kg	4kg	5kg
加入物品1	6	6	6	6	6
加入物品2	6	10	10+6=16	10+6=16	16
加入物品3	6	10	16	16	18

加入物品2时，袋子当前为1kg 的容量时，我们发现物品2装不进去。那我们应该取多少呢？是不是只要取物品进来时1kg最大钱？，当袋子为2kg时，我们发现物品2可以装下去，此时可以得到10块钱，之前物品1进来时2kg最大是6吧，那我们肯定要选择大的这个10，而不是6.此时袋子还剩0kg可以装。

袋子为3kg时，我们还是可以装下这个物品2,得到10块，袋子还剩下1kg。

10+1kg能装的东西。

物品3来了，袋子为4kg时，物品3可以转进来，得到12块钱，袋子还剩0kg。

我发现我不装物品3 还能得到16呢

物品3来了，袋子为5kg时，物品3可以转进来，得到12块钱，袋子还剩1kg。那么装了物品3就能得到12+6=18块钱

我发现我不装物品3 能得到16，比18小，所以决定装。

上面这一个递推过程总结起来就是一个东西------状态转移方程：

能装的时候 每次和上面的比较，大我就装，否则就不装。

Max(money[i]+res[i-1][w-weight[i]],res[i-1][w]);

money[i]+res[i-1][w-weight[i]]:装这个物品

w-weight[i] :表示装完还剩下的空间

res[i-1][w-weight[i]]:表示装完后剩下的空间还能装的最大值，取上一次的结果。

Res[i-1][w]表示不装这个物品的值

和遍历的比较及优化：

遍历每次在物品加进来的时候都会保存选择与不选择两种状态那么这样下去越到后面状态保存的就越多其实就是2^n次，因为每个物品都有选与不选两种情况。而动态规划是每次都会把当前情况下的最优解计算出来，层层递推，下一层的最优解都是基于它上一次结果存下来的，所以最后一个结果就一定是最优解。

其实也是把问题都分解成了一个子问题，然后通过子问题去求解全局最优解。

四、动态规划的总结

一般用动态规划可以解决的问题：

1.局部最优解：也就是它会有一个最优子结构

2.子问题可以重复

3.状态转移方程：通过把问题分成很多小阶段一段段的转移。从而得出最优解.状态转移方程是解决动态规划的关键。如果我们能写出状态转移方程，那动态规划问题基本上就解决一大半了，翻译成代码非常简单。但是很多动态规划问题的状态本身就不好定义，状态转移方程也就更不好想到。

1.求解最值问题：最短路径经典算法

2.短字符相似性匹配

3.策略问题:

4.哈夫曼编码

五、动态规划与贪心算法的比较

五、动归和贪心的比较

写出状态转移方程，那动态规划问题基本上就解决一大半了，翻译成代码非常简单。但是很多动态规划问题的状态本身就不好定义，状态转移方程也就更不好想到。

1.求解最值问题：最短路径经典算法(贪心算法)

2.短字符相似性匹配：相似度，编辑距离(动态规划) 两个字符串求最大公共子串(动态规划)

3.策略问题: 贪心

4.哈夫曼编码: 贪心