自动驾驶 9-5: EKF 的局限性 Limitations of the EKF

Posted 2022-01-08 AI架构师易筋

在最后两个视频中， 我们了解了扩展卡尔曼滤波器或 EKF 以及我们如何 可以使用它使线性卡尔曼滤波器适应非线性系统。

虽然 EKF 可以很好地解决许多实际问题， 有一些重要的限制需要记住 确定 EKF 是否适合您的算法。

在本视频中，我们将讨论其中一些限制。

回想一下，EKF 通过线性化我们的系统来工作 非线性运动和观察模型 更新状态估计的均值和协方差。

线性化模型是 只是真实非线性模型的局部线性近似。

我们称之为之间的区别 近似值和真实模型，线性化误差。

一般来说，任何函数的线性化误差取决于两件事。

首先是原始函数的非线性程度。

如果我们的非线性函数非常缓慢或大部分时间非常平坦， 线性近似将是一个很好的拟合。

另一方面，如果函数变化很快， 线性近似不会做得很好 在函数的大部分域中捕获函数的真实形状。

第二件事线性化误差取决于 on 是您离操作点的距离。

离操作点越远， 线性近似的可能性越大 是偏离真正的功能。

线性化误差的这些特性 EKF 具有重要意义。

那么，让我们看一个例子 线性化误差影响均值和协方差 两个随机变量 由一对常见的非线性函数转换。

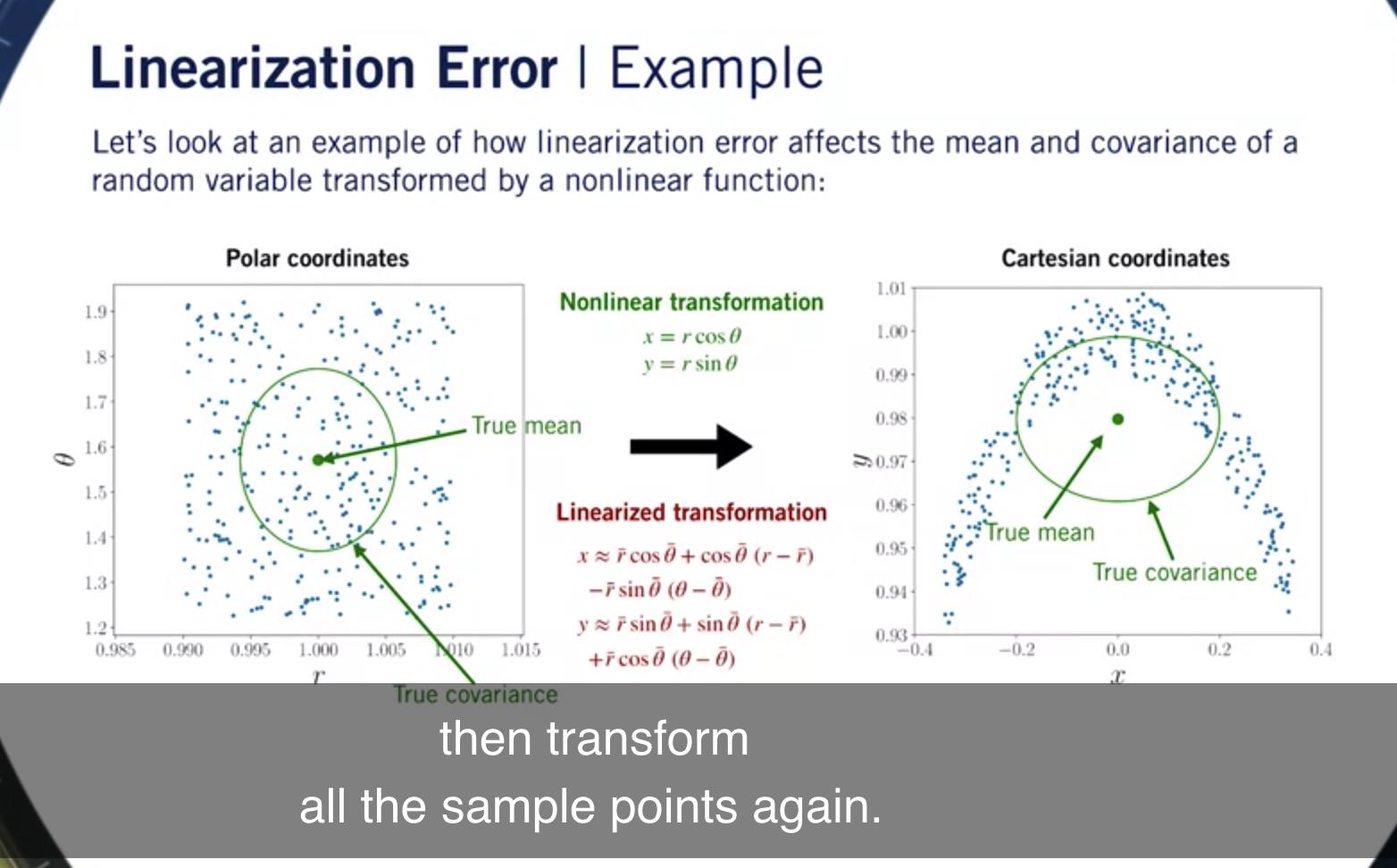
具体来说，让我们看看非线性变换从 极坐标 r 和 Theta 到笛卡尔坐标 x 和 y。

这种变换常用来工作 使用激光扫描仪或 LIDAR， 报告范围和方位测量值， 就像许多自动驾驶汽车上的扫描仪一样。

让我们从一些样本中 区间上的均匀分布 极坐标并考虑当我们 将样本转换为笛卡尔坐标。

为了说明这是什么样子， 我们已经绘制了来自的随机样本 均匀分布为您在左侧看到的蓝点。

当我们变换每个样本点时 到相应的笛卡尔坐标， 我们看到变换分布呈现香蕉形状， 显示在右侧。

显然，香蕉分布的形状不是 仅使用均值和协方差来完全捕获。

但是让我们看看原始 PDF 的均值和协方差会发生什么变化。

在左边的图中， 均匀分布的真实平均值是 显示为中间的绿点， 真正的协方差由绿色椭圆表示。

将均匀分布转化为笛卡尔坐标后， 输出分布的平均值在这里结束， 它的协方差看起来像这样。

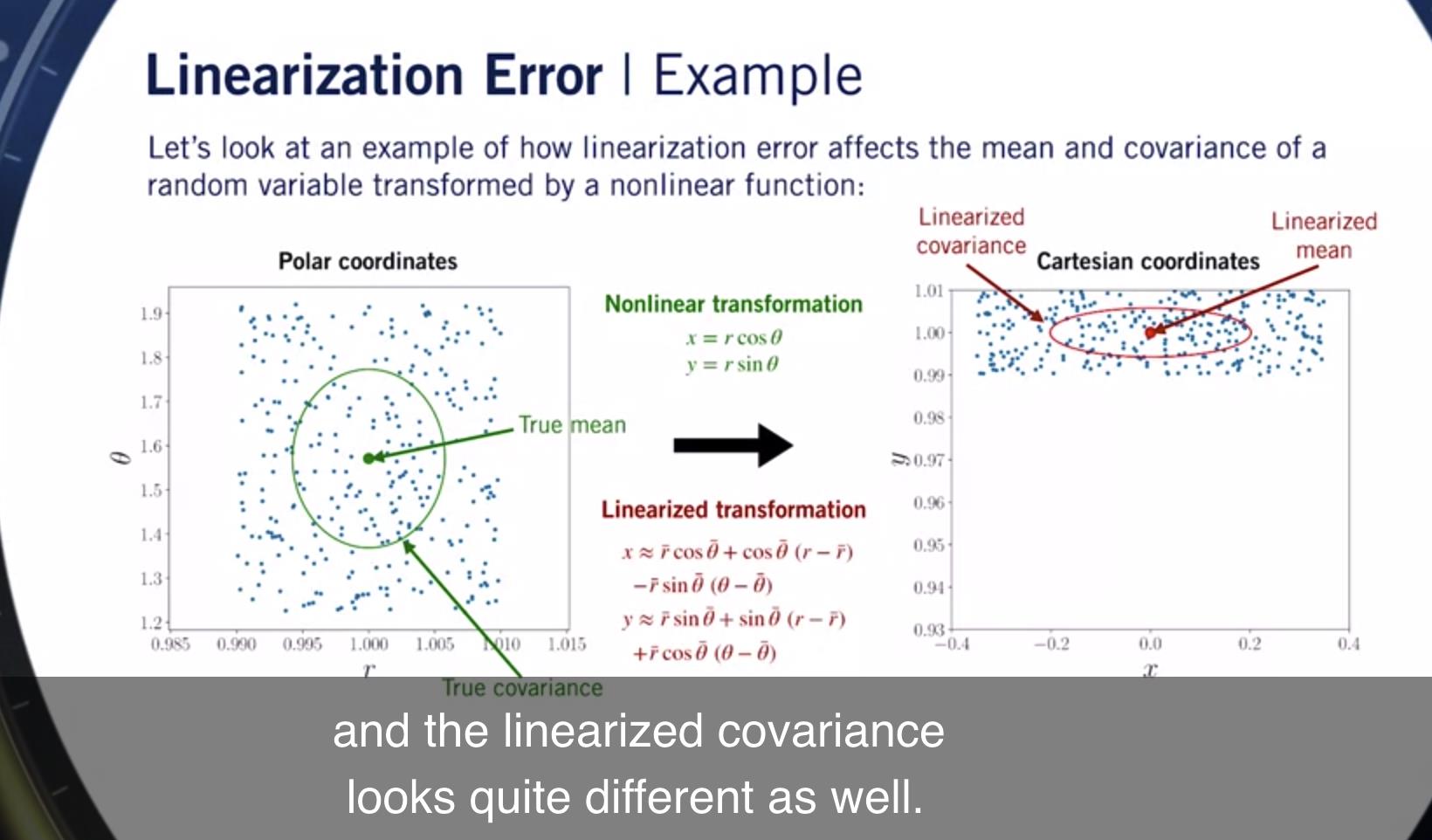
现在，考虑一下如果我们线性化会发生什么 极坐标到笛卡尔变换 关于原始分布的均值和 然后再次变换所有样本点。

线性化变换给了我们 看起来像的输出分布 另一个均匀分布和熊 与我们之前看到的香蕉形分布几乎没有相似之处。

如果我们看一下这个分布的平均值， 用红点表示， 它降落在这里的某个地方， 并且线性化的协方差看起来也大不相同。

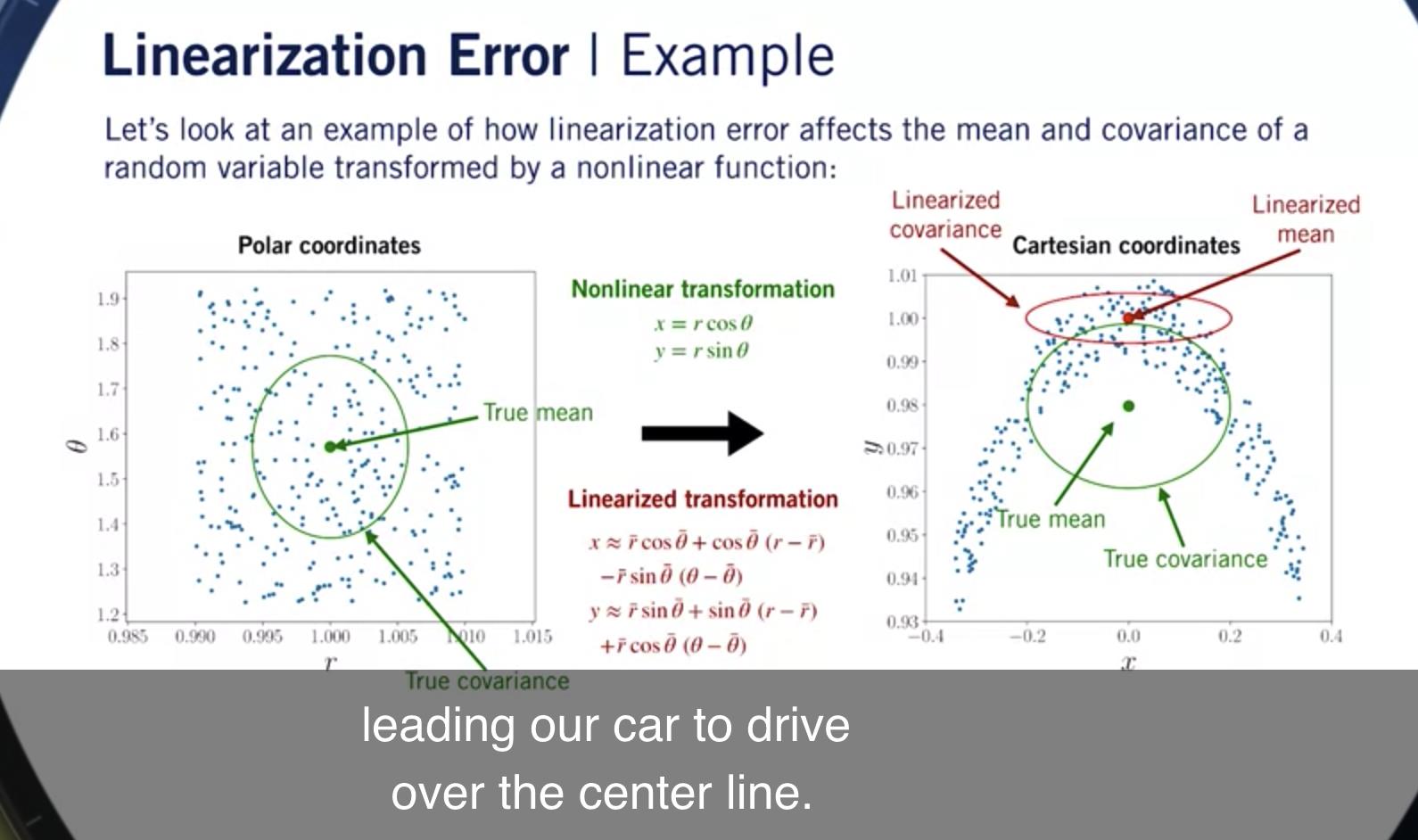
让我们比较线性化和非线性输出分布。

你可以看到 线性分布在 与真正的平均值非常不同的地方， 并且线性化协方差严重低估 真实输出分布沿 y 维度的分布。

所以，在这种情况下， 我们可以看到线性化错误会导致 我们对输出分布完全没有达到目标的信念， 这可能会导致我们的估算器出现大问题。

例如，从产生的车道标记的估计位置 激光扫描仪可能与实际位置有很大不同， 带领我们的车驶过中心线。

那么什么时候线性化是 EKF 的问题呢？

有两种情况需要注意。

第一种是当您的系统动力学高度非线性时。

如果你的情绪和测量模型接近线性， 线性化误差不会是一个大问题。

但如果不是，您的线性化估计器将不会 做好捕捉系统真实行为的工作。

第二种情况与距离多远有关 您尝试使用线性化模型的操作点。

对于移动非常频繁的自动驾驶汽车 相对于传感器的采样时间快， 与缓慢移动相比，您将获得更多的线性化误差。

从数学上讲，有 EKF 中线性化误差的两个重要后果， 我们在前面的例子中看到了这两者。

一是估计均值可以 与真实状态大相径庭， 另一个是估计的协方差可能 无法准确捕捉状态中的真实不确定性。

换句话说，这意味着线性化错误会导致 我们的估计器对完全错误的答案过于自信。

在最坏的情况下， 估计量可能会发散， 也就是说，完全丢失并且无法提供有用的输出。

更糟糕的是，一旦像 EKF 这样的估计量出现分歧， 它不能被拉回正轨。

通常，如果可以，您将被迫重新初始化。

这是一个巨大的问题 我们在处理自动驾驶汽车时的安全性。

如果您的汽车的估算器在驾驶时发散， 它可以很容易地驶离道路进入 沟或与另一辆车发生碰撞。

因此，线性化误差是 EKF 的主要理论限制。

但是还有其他一些常见的问题，我们会 在我们的实现中遇到。

可能在实践中最常见的问题是它很容易 当我们计算雅可比矩阵时出错， 特别是当我们处理一个复杂的非线性系统时。

我不能告诉你我的学生和 我在推导雅可比时遗漏了一个减号。

这可能会导致许多小时的调试。

有些人试图绕过 这个问题通过使用数值微分在 运行时或编译时的自动微分。

但这些都有其自身的缺陷，有时会出现不可预测的行为。

最重要的是，如果一个或 我们的更多模型甚至无法区分， 就像步进电机的阶跃函数响应一样。

所有这些缺点都让我们产生了一个问题：我们是否 真的需要线性化来做非线性卡尔曼滤波吗？

总结一下这个视频， 扩展卡尔曼滤波器有 基于其使用分析局部线性化的几个限制。

如果正在建模的系统的动力学高度 非线性或线性化误差大， 过滤器可能会发散。

EKF 要求雅可比矩阵为 计算，这通常是一个乏味且容易出错的过程。

尽管如此，EKF 是一种经过验证的工具 状态估计，您将毫无疑问 作为自动驾驶汽车工程师经常遇到它。 在下一个视频中，我们将讨论 另一种常见的滤波器变体称为无迹卡尔曼滤波器， 这在很大程度上解决了 EKF 的这些局限性。

参考

https://www.coursera.org/learn/state-estimation-localization-self-driving-cars/lecture/OCrZc/lesson-5-limitations-of-the-ekf