根据一个数组，判断是否是二叉搜索树的后序遍历序列

Posted 2022-01-07 ohana！

题目内容：

 分析：

• 先从二叉搜索树入手

1. 什么是二叉搜索树？二叉搜索树的特点又是什么？首先，关于根结点，左子树的值域全都小于根结点，右子树的值域全都大于根结点，当以其中一个结点看做是根结点，依然满足。其次，二叉树搜索树的中序遍历结果是有序的并且递增

• 在讨论后序遍历（主要针对于二叉搜索树）

1. 后序遍历的特点是什么？一个二叉树的后序遍历结果，其最后一个元素就是这个二叉树的根结点，如果是二叉搜索树的话，那么会有一个临界点，这个临界点左边的所有元素都小于根结点，从临界点开始，到除去最后一个元素，都是大于根节点，一旦出现临界点左边有元素大于根节点或者临界点右边有元素小于根节点，那么这个树一定不是二叉搜索树

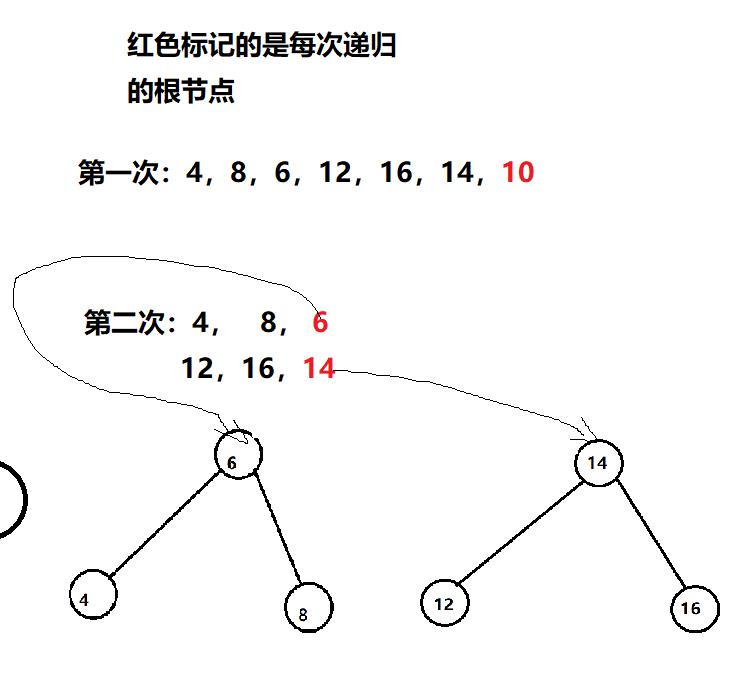
• 回归本题，其目的是从后序遍历判断是否是二叉搜索树，我们就可以顺水推舟，从刚才的特性入手，我们可以利用递归，将每一次的递归看做是一个二叉搜索树，那么，只需用满足我们上述所说的特性即可，每次只用更新下标进行判断

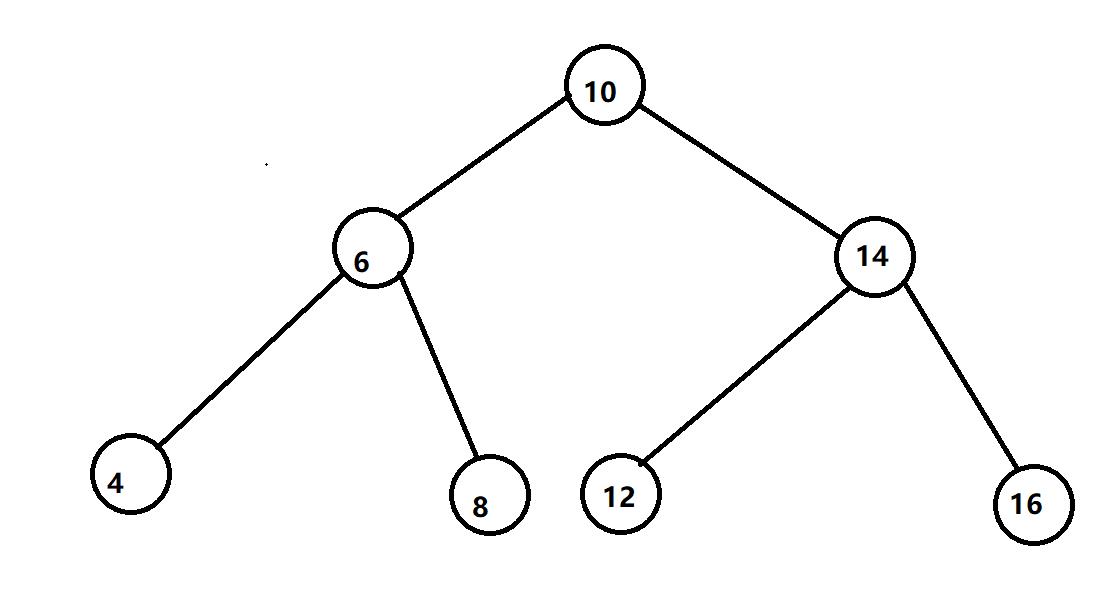
  步骤	数组序列	根节点	左子树	右子树
  1	【4，8，6，12，16，14，10】	【10】	【4，8，6】	【12，16，14】
  2	【4，8，6】	【6】	【4】	【8】
  3	【12，16，14】	【14】	【12】	【16】

  
• 基本思路和解题过程详见代码注释 
• 

解题代码：

public class Solution 
    public boolean  postOfBST(int[] sequence,int first,int left)
        //根据下标进行判断，如果到这里还没return false，说明就是的，直接返回true
        if(left - first <= 0)
            return true;
        
        /*
        1.定义begin，我们需要知道的是，对于这个递归条件来说，有两个点是不能变的
          那就是first和分割成新“二叉搜索树的第一个下标”2，从一个二叉搜索树的逐层剥离来说
          最左侧的结点一定是不会变化，因此，判断也是从右向左进行，每次变化的是根结点的位置
          具体图解，在上面的分析里面会有呈现
        */
        int begin = first;
        /*
        1.这里的作用是为了记录最后一个结点，就是每一个二叉树的根结点的值域
        2.为什么记录，就是为了下面的判断条件进行铺垫，在分析中也说了关于根结点的特性
          递归思想也由此而来，为了明白前一部分是不是二叉搜索树，那么就得，判断前一个是不是满足根结点的特性
        */
        int root = sequence[left];
        //进行循环，找到那个临界点，为下一步的判断继续创造条件
        //并且，在这个位置已经将小于root的元素排除掉了，可以说，从这里开始就是根结点的临界点
        while(begin < left && sequence[begin] <= root)
            begin++;
        
        /*
        1.开始进行判断
        2.如果从begin所在的位置开始，有大于root的就一定是不符合条件的
        */
        for(int i = begin;i < left;i++)
            if(sequence[i] < root)
                return false;
            
        
        //进行递归，将其分为两部分开始判断
        return postOfBST(sequence,first,begin - 1) && postOfBST(sequence,begin,left - 1);
    
    public boolean VerifySquenceOfBST(int [] sequence) 
        /*
        本题主要思想还是利用递归，相比于其他解法，主要是更好理解大致过程
        具体细节是在递归的条件和边界上，比较难，但是，递归也是一部分一部分进行的，把握好就行
        1.定义数组的长度为len，并进行判断
        2.如果是0，说明没有元素，即肯定不是二叉搜索树的后序遍历序列
        3.如果是1，就说明只有一个元素，那么就说明只有根节点一个结点，那么也是二叉搜索树
        */
        int len = sequence.length;
        if(len == 0)
            return false;
        
        if(len == 1)
            return true;
        
        //开始进行递归
        return postOfBST(sequence,0,len - 1);