神经网络为什么可以（理论上）拟合任何函数？

Posted 2023-03-14 AI有温度

原文链接：用小学数学带你感受人工智能的魅力

在ChatGPT火爆出圈后，越来越多的人对人工智能、深度学习、神经网络等名词更加好奇，身边的朋友最近也频繁的问我，AI究竟为什么如此强大？今天我就用大家都看得懂的小学数学知识，来带大家感受人工智能的魅力，带大家认识神经网络。

平面中的一条直线能分割平面

平面中的一条直线，可以用函数$y=kx+b$来表示，比如$y=x-2$：

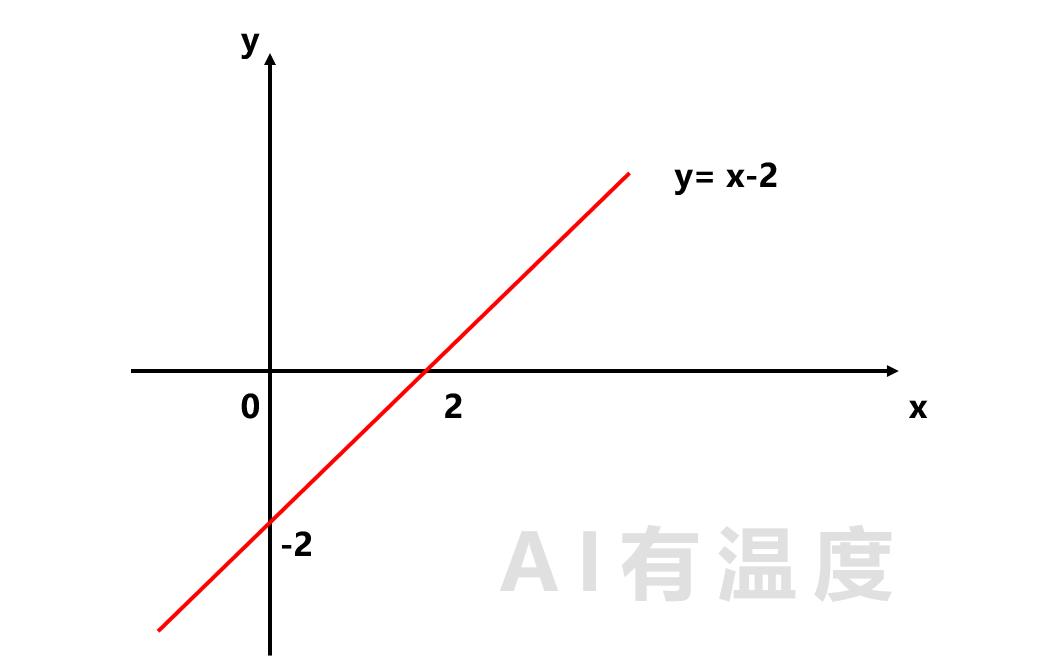
这条直线也可以表示为$y-x+2=0$，以线为依据，它可以将平面分为直线上（阴影部分）和直线下两部分。

如果随机给你一个点，你如何判断它在直线上方还是直线下方呢？

我们以(2,2)和(2,-2)两点为例：

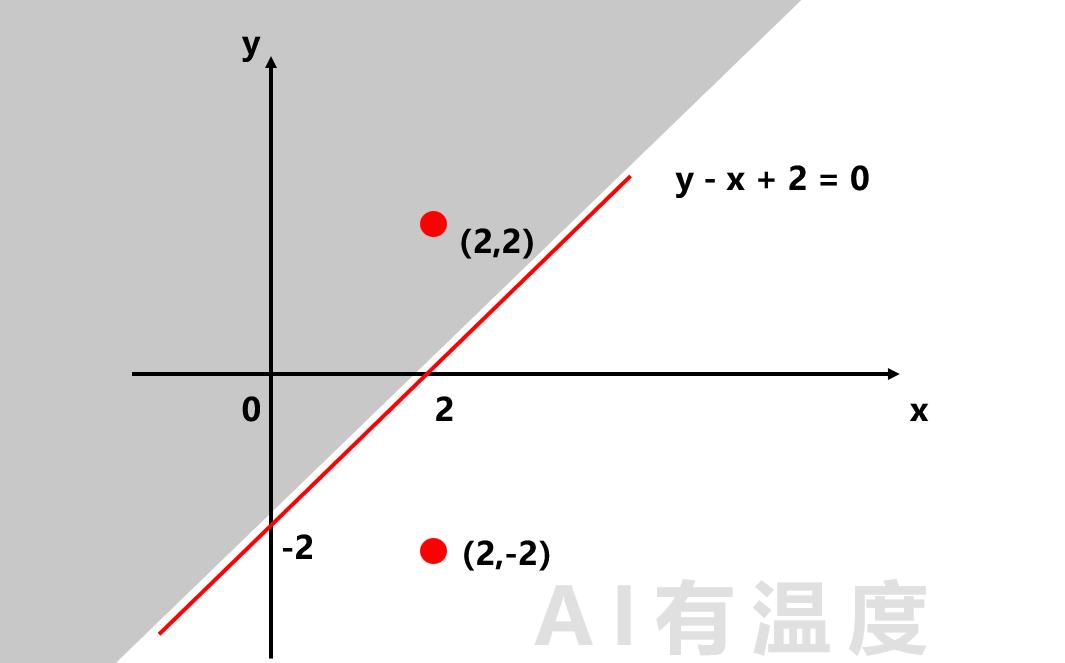
将点(2,2)代入方程$y-x+2=0$：
$$2-2+2=2$$

将点(2,-2)代入方程$y-x+2=0$：
$$-2-2+2=-2$$

不难发现，将直线上方的点代入方程后，最终结果会大于0；将直线下方的点代入方程后，最终结果会小于0。

我们用z来表示方程的结果$z=y-x+2$，可以得出以下结论：

• 随机带入一个点，当z大于0时，说明点在直线的上方
• 随机带入一个点，当z小于0时，说明点在直线的下方

那么我们只要再构造一个函数来判断z的值是大于0还是小于0，即可判断该点在图中的位置。

判断函数怎么构造

随机带入一个点：

• 如果它在直线上方（z大于0），我们就令它为真，让判断函数输出1
• 如果它在直线下方（z小于0），我们就令它为假，让判断函数输出0

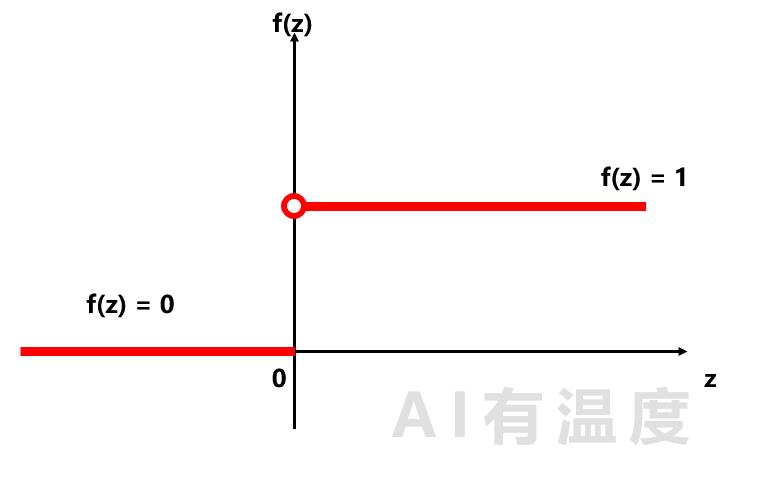
判断函数的表达式是：
$$f(z)=\begin{array}{l}0,z\le 0\\ 1,z>0\end{array}\text{\hspace{1em}(1)}$$

我们把任意一个点(x,y)带入$z=y-x+2$后可以求得z的大小，再将z作为判断函数的输入，就可以输出0或1，来直接得出这个点位于直线的上方还是下方。用流程图来表示：

比如将(2,2)代入：

所以任意给出平面一点，只要先代入函数$z=y-x+2$算出z的值，再将z的结果代入判断函数，就可以知道它在直线的上方还是下方。

在AI领域，这个判断函数叫做激活函数。

从一条线到三角区域

如果你会判断一个点位于直线的上方还是下方，那么你会判断一个点位于三角形内（阴影部分）还是三角形外吗？

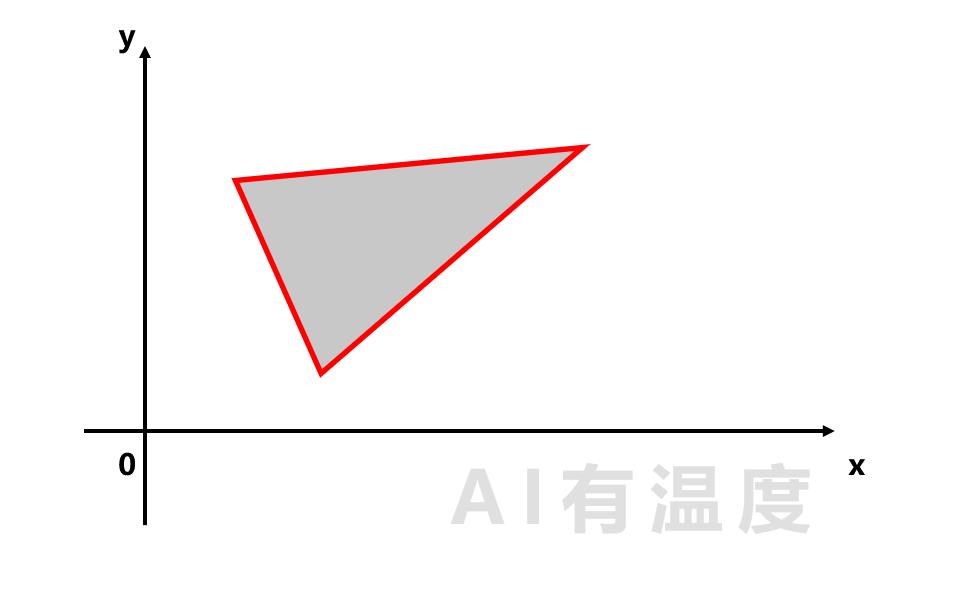
不难想到，可以根据这个点位于三条线的位置来判断！

由上图可知：

设L1的方程是$k_{11}y+k_{12}x+b_1=0$，并规定当点在L1右方时（阴影部分）为真

设L2的方程是$k_{21}y+k_{22}x+b_2=0$，并规定当点在L2下方时（阴影部分）为真

设L3的方程是$k_{31}y+k_{32}x+b_3=0$，并规定当点在L3左方时（阴影部分）为真

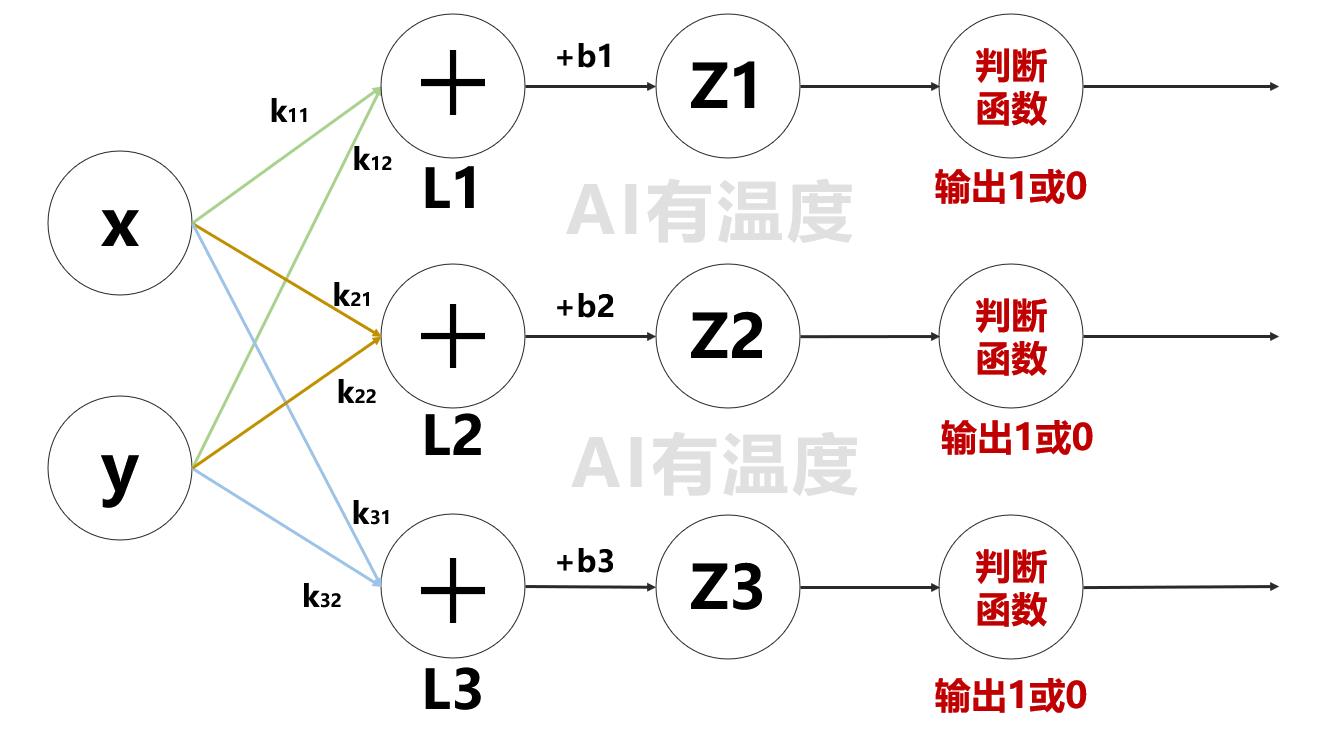
根据上文一条直线的例子，我们不难理解，当三个判断函数的输出均为1时，这个点就在三角形内部。
因此，我们需要对三个判断函数输出值是否均为1进行二次判断。

我们可以把三个判断函数的输出看作新的输入，再经过一次线性变化和判断函数，$z_4=k_{4}f(z_1)+k_{5}f(z_2)+k_{6}f(z_3)-2.5$。

最后让它输出0或1，来判断一点是否在三角形内部。因为判断函数的输出只能是0或1，所以将他们相加后，结果可能的最大值为3，然后减去一个(2,3)区间内的数，这里选的是2.5（截距b），最后通过判断函数，就可以判断一点是否在三角形内了。

从三角形到圆

如果会判断一个点是否在三角区域内，那么你会判断一个点在矩形内吗？

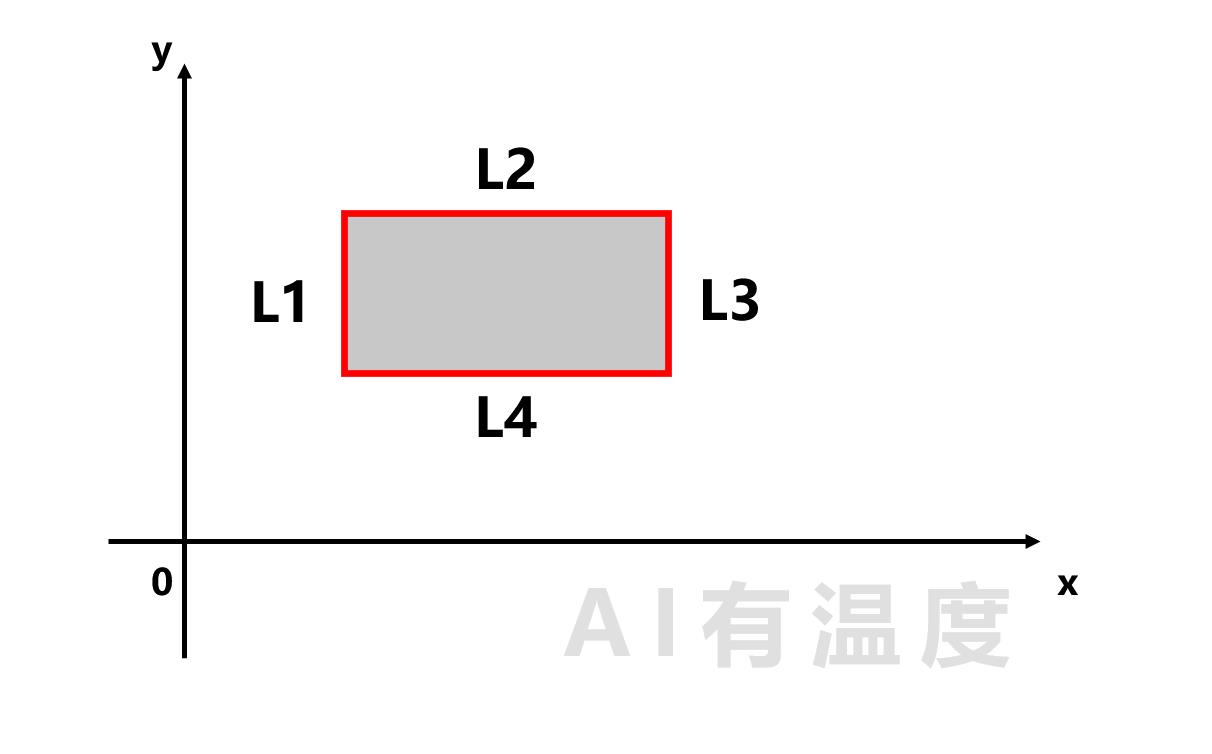
无非就是再多加一条线：

如果这个区域是圆呢？

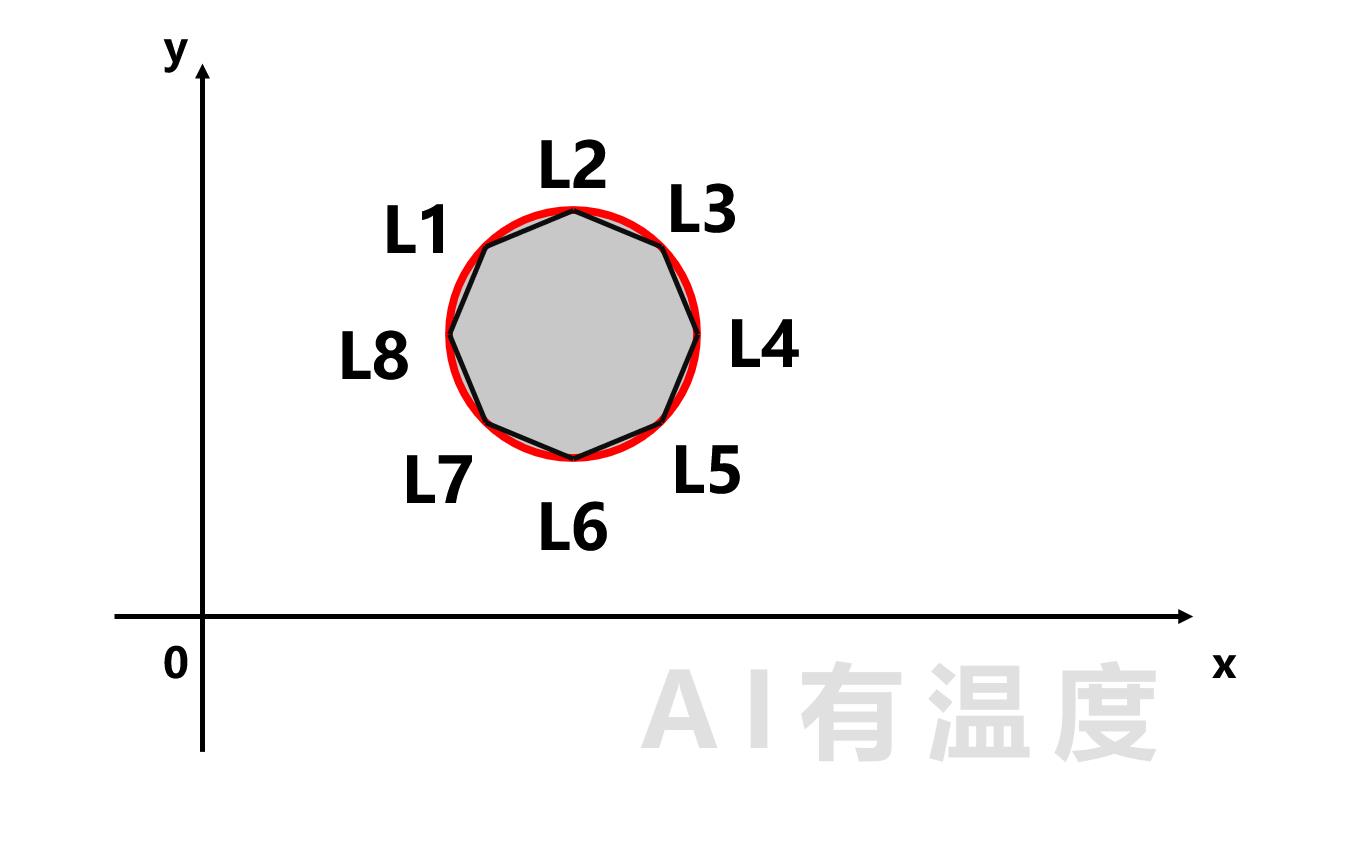
我们就可以用8条直线乃至更多直线去拟合这圆，然后判断该点是否在这些直线内部：

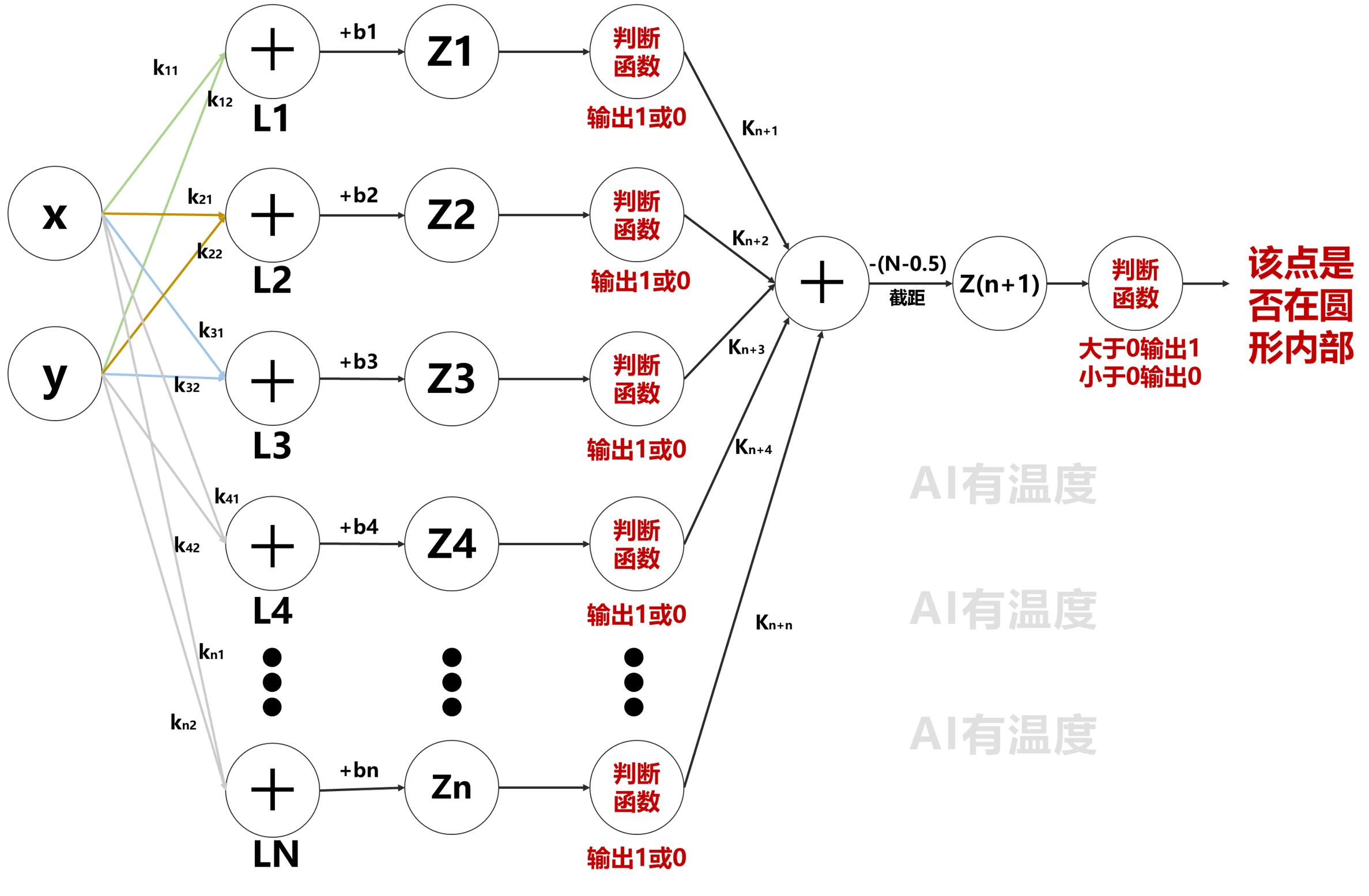
同理，只要每层的直线够多，我们就可以拟合任意图像：

原文链接：用小学数学带你感受人工智能的魅力

科普：人工智能中一层神经网络包括一次连续线性变化与非连续线性变化。

连续线性变化就是$y=kx+b$，要求连续且为直线。将输入的x乘系数后再加上截距，使它变大或变小，在图中为一条直线。

非连续线性变化就是判断函数，在人工智能领域称为激活函数。比如我们本次用的判断函数在0处是间断的，不是连续的。

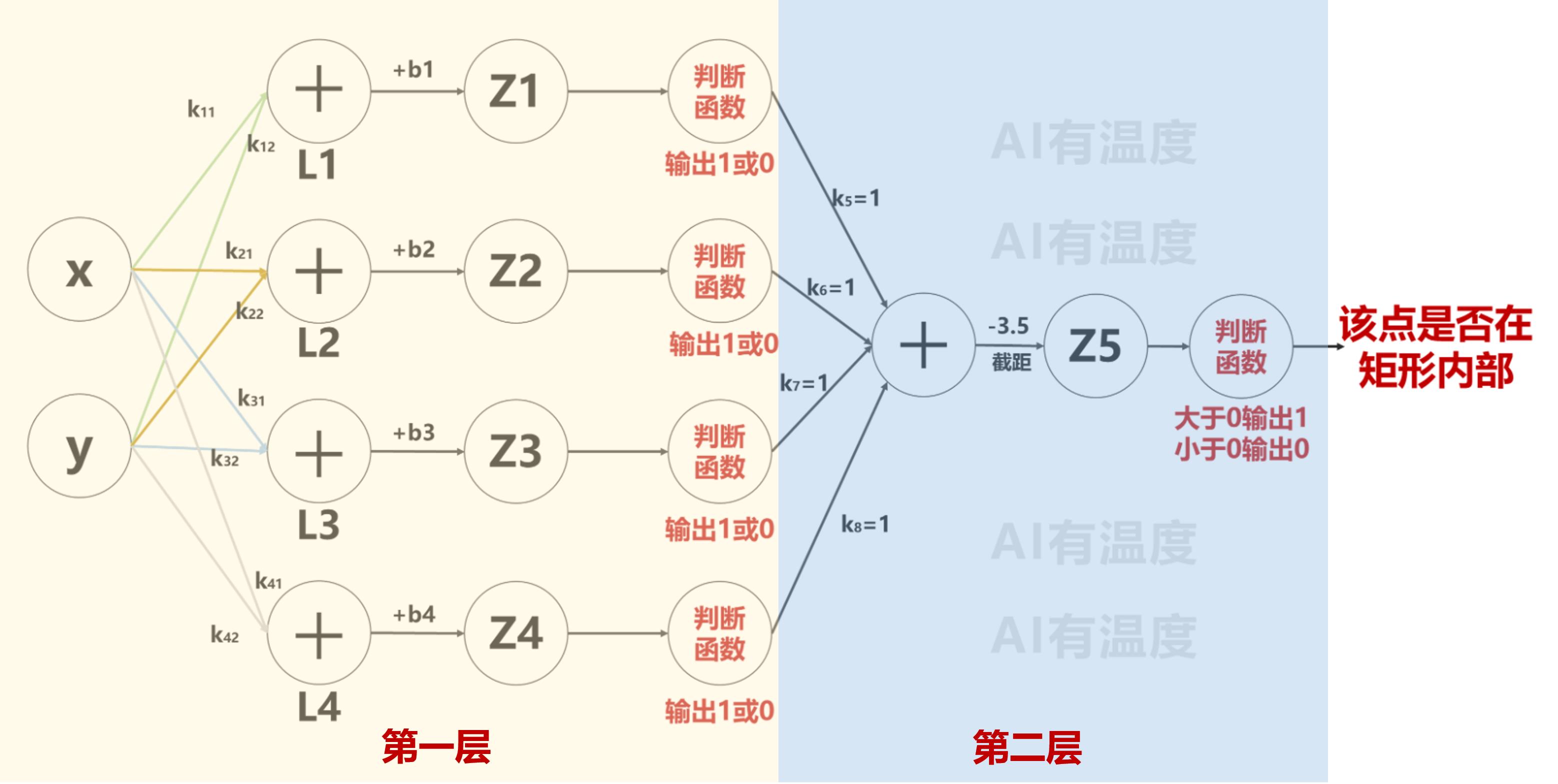
我们处理以上问题时，都用了两层神经网络，大家知道是哪两层吗？

以判断一点是否在矩形内为例：

从一个图形到多个图形

那么如果是要判断一点是否在以下阴影区域呢？

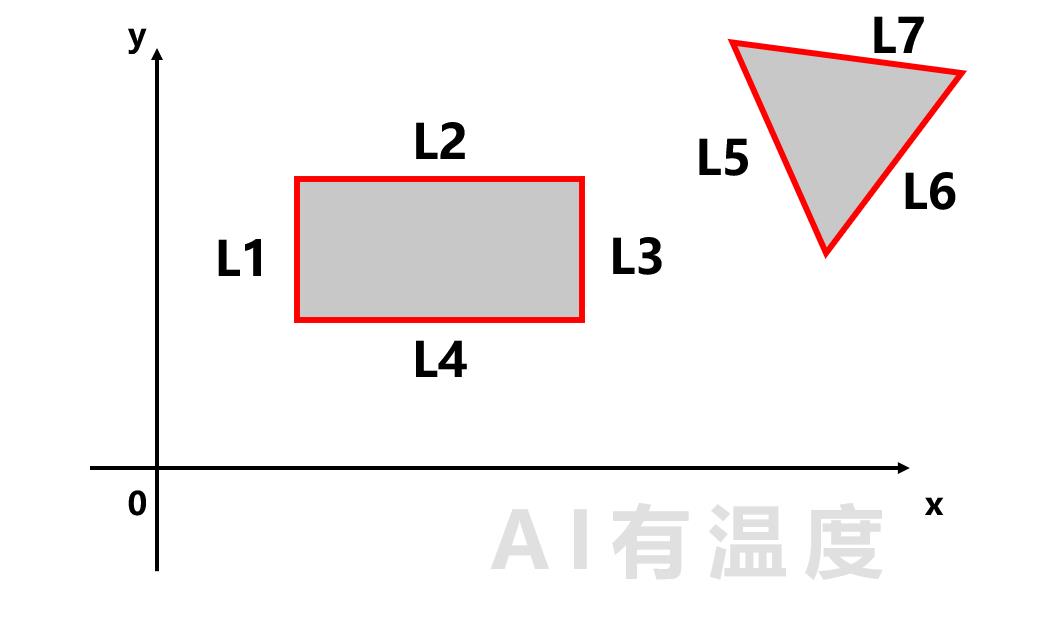
那就需要用4条直接拟合矩形，3条直线拟合三角形，把他们的结果汇总，需要再加一层神经网络($z10$)：

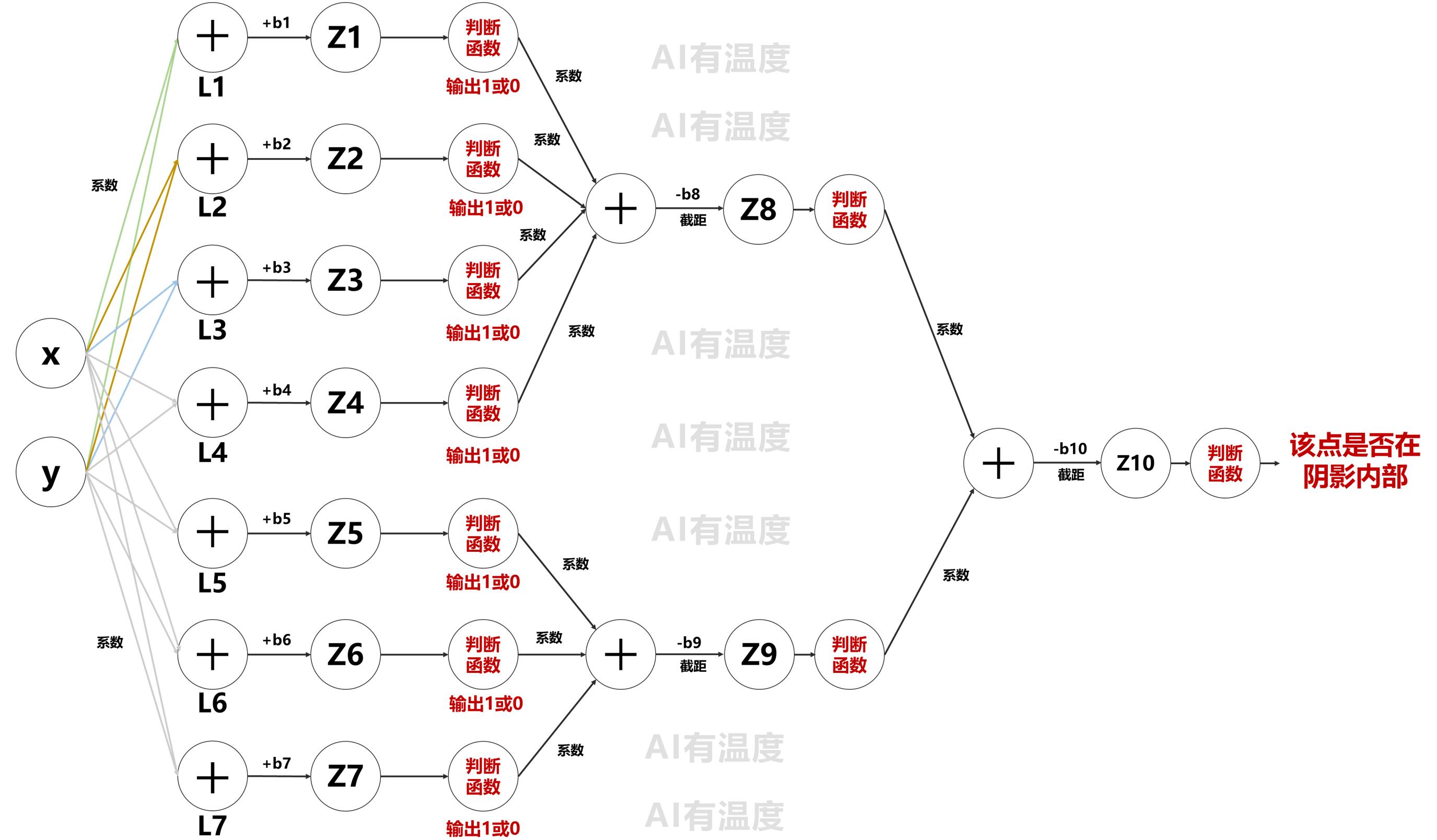
有了这个例子，在二维平面内的所有问题（任何形状、任意多少区域）都可以使用3层神经网络来解决，比如：

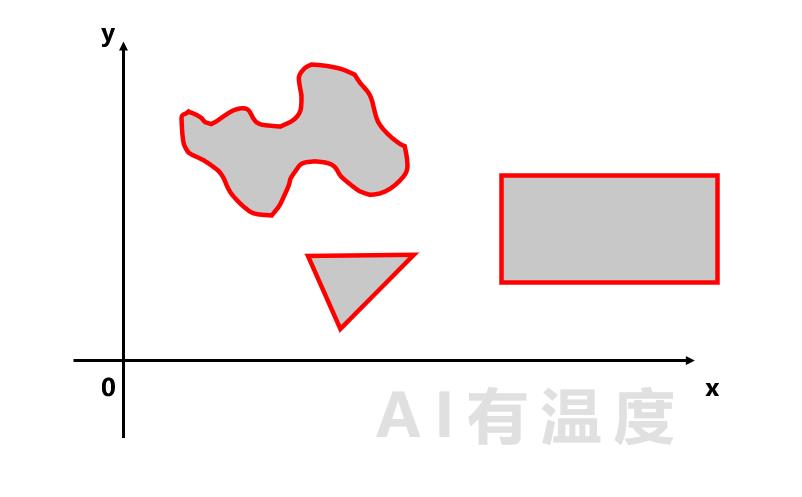
这就是人工智能领域著名的结论：三层神经网络可以模拟任意决策面。这就是深度学习（神经网络）的基础。

神经网络的精妙之处在于，将前一层的多个输出值再次构造成一个新的线性函数从而进行再判断，以此类推。神经网络不断从线性变为非线性的过程，就是提取数据特征的过程。

从二分类到多分类

此上介绍的问题都是二分类问题（在阴影中或不在阴影中），但生活中绝大多数问题都是多分类问题。比如如何判断一点在以下哪个区域？这就是一个三分类问题。

几分类问题就设置几个输出，最后哪个判断函数的输出为1，该点就在哪个区域：

原文链接：用小学数学带你感受人工智能的魅力

从二维到多维

我在AI科普4：通俗易懂的机器学习模型中举例的肿瘤问题：有一批肿瘤病人相关数据，横轴为肿瘤存在时长，纵轴为肿瘤的大小，橙色为恶性肿瘤，绿色为良性肿瘤。每位病人肿瘤的大小和存在时长就构成了二维空间中的一个点，现在我们有10位病人的肿瘤病情信息。

如果新来一位病人，我们怎么判断它是良性还是恶性呢？这个问题我们就可以用神经网络去解决。

构造一条线（曲线也可以），这条线是$k_{1}y+k_{2}x+b=0$，它可以将良性肿瘤与恶性肿瘤分开：

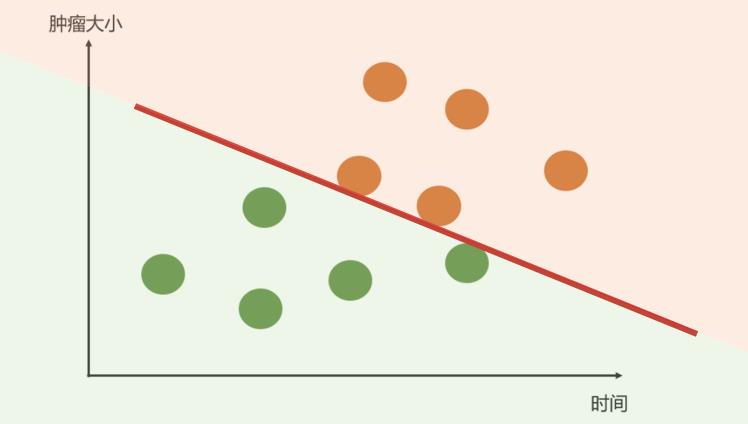
新来一位病人，他得肿瘤的时长是x，目前大小是y，就把它代入神经网络$z=k_{1}y+k_{2}x+b$。

如果z大于0，在直线上方，就为恶性；在直线下方，就为良性。

实际问题中，只要考虑的因素更多，数据的维度变多，也就意味着输入更多。比如进行电影评分预测（结果分为5个等级），那么一部电影要考虑的因素可能包括电影类型、导演、演员、电影时长等等。我们就把这些因素设为输出，将5个结果设为输出：

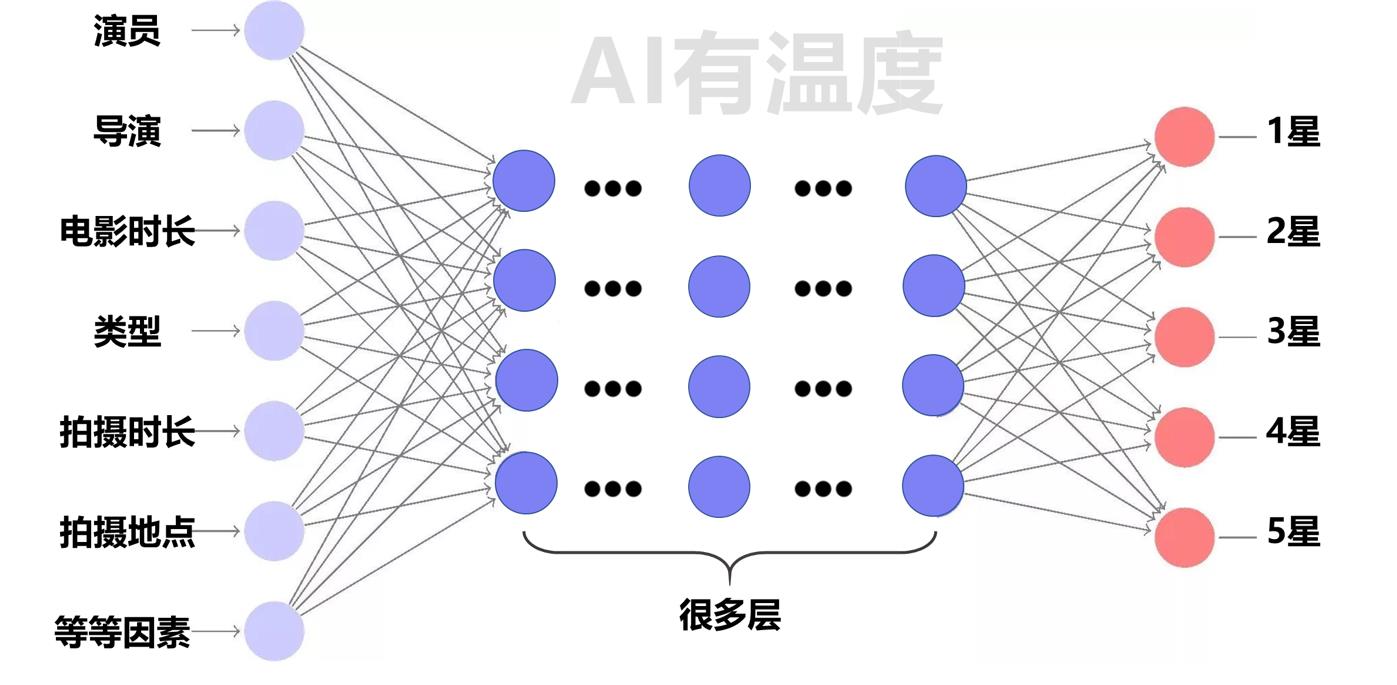
这个过程，是不是很像我们大脑的思考过程？其实神经网络就是根据人脑来设计的模型。例如当我们要买一件短袖，我们会参考品牌、价格、款式、颜色等维度综合考量，得出买或不买的结论。

这就是人工智能的强大之处，只要直线个数够多、维度够多，就可以拟合任意空间，解决任何问题。比如现在的ChatGPT，就有1750亿个参数。

难点就是学习这些参数

以一点是否在三角形中的函数为例$z_4=k_{4}f(z_1)+k_{5}f(z_2)+k_{6}f(z_3)-2.5$：

我们可以轻松发现，解决某点是否在三角形内这个问题时，只要让$k_4=k_5=k_6=1$，$b$

MATLAB神经网络的目录

学习笔记TF026:多层感知机

一：输入层隐藏层输出层；二隐藏层的层数

什么是生成对抗网络？

用matlabBP神经网络做多元线性回归，求问各参数的拟合值怎么看？