[计算机数值分析]迭代法求根过程的加速

Posted 2022-01-06 Spring-_-Bear

问题描述

对于收敛的迭代过程，只要迭代足够多次，就可以使得结果达到任意精度，但有时迭代过程收敛缓慢，从而使计算量变得很大，因此对迭代过程加速的研究显得尤为重要。
设 х₁ 是根 х﹡的某个近似值，用迭代公式校正一次得：x₁′ = f(х₁)，假设f(x)的一阶导数在所考察得范围内改变不大，其估计值为 L，则有 х﹡ -x₁′ ≈ L(x -х₁)，由此解出 х﹡ ≈ 1.0 / (1 - L) × x₁′ - L / (1 - L) × х₁。也就是说，如果将迭代值一次的值 x₁′ 与迭代初值 x₁ 进行加权平均，可以期望所得到得解是比 x₁′ 更好得近似根。
总的来说，通过给定估计值L的控制，对一次迭代值跟迭代初值进行加权平均，我们有理由相信加权后的解相比加权前的解可以是更好的近似根。

运行示例

此为未对迭代过程加速，找到符合精度要求的近似根，需要迭代9次

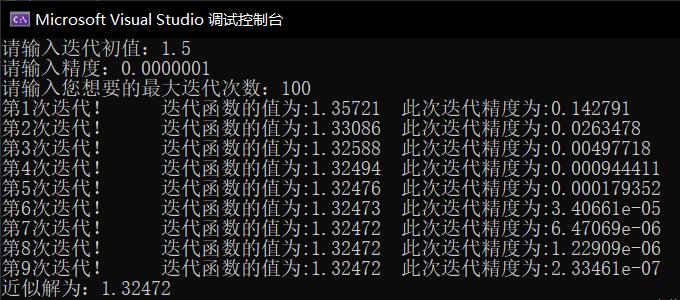
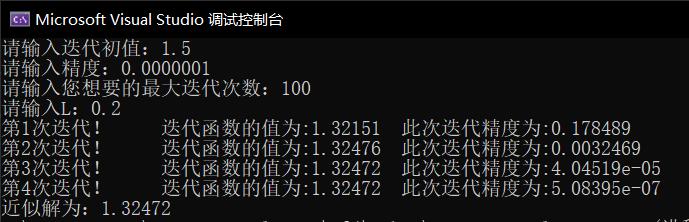
此为加速迭代过程，估计值L取0.2,迭代4次后找到符合精度要求的根。显然，加速的效果是显著的

源码

//程序实现用迭代法求方程的根
#include<iostream>
#include<cmath>
using namespace std;

//用户自定义的迭代函数f(x)
double function(double x)

	double result = pow(x + 1, 1.0 / 3);
	return result;


int main(void)

	double x0, x1, x2, accrucy, item, L;   //x0为迭代初值，x1=f(x0);accrucy为精度;L为估计值;x2为加权后的近似解
	int n, k = 1;   //n为允许的最大迭代次数

	cout << "请输入迭代初值：";
	cin >> x0;
	cout << "请输入精度：";
	cin >> accrucy;
	cout << "请输入您想要的最大迭代次数：";
	cin >> n;
	cout << "请输入L：";
	cin >> L;

	do 
	
		x1 = function(x0);

		x2 = 1.0 / (1 - L) * x1 - L / (1 - L) * x0;   //对迭代值x1与x0进行加权平均得到x2

		if (abs(x0 - x2) < accrucy) //根的近似解符合要求，输出近似根
		    
			cout << "近似解为：" << x2;
		
		else     //继续下一次迭代，直至找到符合精度要求的根或最大迭代次数用完
		   
			if (k > n)    //允许迭代n次，当迭代次数大于n时结束迭代
			    
				cout << "迭代次数耗尽，迭代结束！\\n未找到符合精度要求的根！！！" << endl;
				break;
			
			else 
			
				//输出本次迭代信息
				cout << "第" << k << "次迭代！\\t迭代函数的值为:" << x2 << "\\t此次迭代精度为:" << abs(x2 - x0) << endl;
				//交换x0与x2,为下一次迭代做好准备
				item = x0;
				x0 = x2;
				x2 = item;
				k++;
			
		
	 while (abs(x0 - x2) >= accrucy);   //循环进行条件为找到的根不符合精度要求

	return 0;