Codeforces Round #760 (Div. 3)

Posted 2022-01-06 MangataTS

A. Polycarp and Sums of Subsequences(思维)

题意

给你七个数，这个数是一个集合元素数为3的所有非空子序列和，求任意满足要求的这个集合

思路

很明显最小和第二小的元素一定是单独的，然后最大的元素一定是三个元素之和，那么直接用最大的元素减去最小的元素即可获得该集合的第三个元素

Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+10;
ll a[N];
int n;


int main()

	int t;
	scanf("%d",&t);
	while(t--) 
		for(int i = 1;i <= 7; ++i) 
			scanf("%lld",&a[i]);
		
		sort(a+1,a+8);
		printf("%lld %lld %lld\\n",a[1],a[2],a[7]-a[1]-a[2]);
		
	
	return 0;

B. Missing Bigram（模拟）

题意

给你$n-2$个由a、b构成的有序的二元组字符，希望你补充一个满足条件的二元组让这个单词连接起来，当前二元组的第二个元素是下一个二元组的开头：

eg:ab ba => aba

思路

因为题目是有序的，我们只用处理没有连接的位置即可，我们只需要判断如果不相连我们就要将下一个元素的第一个位置放答案里面，否则我们加入下一个元素的第二个位置，最后别忘了判断是否进行过添加，如果没有则随便在末尾添加一个元素即可

Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+10;
int n;

string ch[N];


int main()

	int t;
	cin>>t;
	while(t--) 
		cin>>n;
		for(int i = 1;i <= n-2; ++i) 
			cin>>ch[i];
		
		string ans = ch[1];
		bool fg = true;
		for(int i = 2;i <= n - 2; ++i) 
			if(ch[i][0] != ch[i-1][1]) 
				fg = false;
				ans+=ch[i][0];
			
			ans += ch[i][1];
		
		if(fg) ans+='a';
		cout<<ans<<"\\n";
		
	
	return 0;

C. Paint the Array（数学）

题意

找到一个d，使得奇数位置的或者偶数位置全都能被整除另一方则全都不能被整除，如果没有则输出0

思路

很显然，这是让我们找奇数位置所有元素的最大公因数和偶数位置所有元素的最大公因数，然后我们将奇数位置的公因数在偶数位置遍历判断一边，再将偶数位置的公因数在奇数位置判断一边，如果有一个满足，那么就找到了，如果都没满足那么就输出0

Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+10;
ll n;
ll a[N];

int main()

	ll t;
	scanf("%lld",&t);
	while(t--) 
		scanf("%lld",&n);
		for(int i = 1;i <= n; ++i) 
			scanf("%lld",&a[i]);
		
		ll one = 0;
		ll two = 0;
		for(int i = 1;i <= n; i+=2) 
			one = __gcd(one,a[i]);
		
		for(int i = 2;i <= n; i+=2) 
			two = __gcd(two,a[i]);
		
		bool fg = true;
		for(int i = 1;i <= n; i+=2) 
			if(a[i] % two == 0) 
				fg = false;
				break;
			
		
		if(fg) 
			printf("%lld\\n",two);
			continue;
		
		fg = true;
		for(int i = 2;i <= n; i+=2) 
			if(a[i] % one == 0) 
				fg = false;
				break;
			
		
		if(fg) 
			printf("%lld\\n",one);
			continue;
		
		puts("0");
 	

	return 0;

D. Array and Operations（贪心）

题意

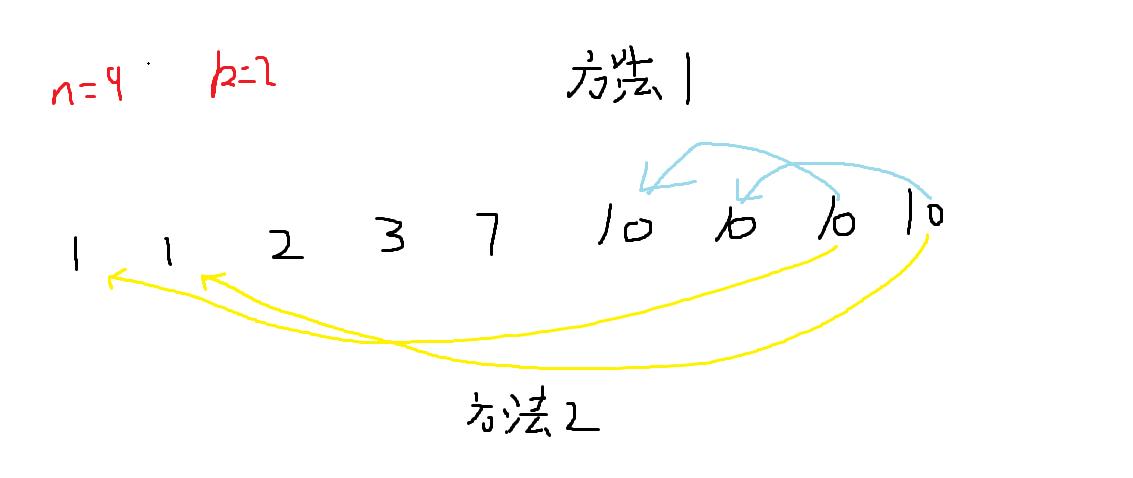
k次操作，每次操作选择两个位置不同的数，然后相除，并向下取整加入答案，最后将剩下的元素加入答案，求最小的答案

思路

很显然，一道贪心题，我们可以有两种贪心的方法，然后去一个min即可

• 我们将后2*k位进行一个运算，即最后一位匹配n-k位置，倒数第二位匹配n-k+1位，然后再将前面的元素加入答案

• 我们将前k位和最后k位进行一个运行，即最后一位匹配第k位，……

• 最后答案去一个min即可

Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+10;
ll n,m;
ll a[N];

int main()

	ll t;
	scanf("%lld",&t);
	while(t--) 
		scanf("%lld%lld",&n,&m);
		for(int i = 1;i <= n; ++i) 
			scanf("%lld",&a[i]);
		
		sort(a+1,a+1+n);
		ll ans1,ans2;
		ans1 = ans2 = 0;
		for(int i = 1;i <= n - 2 * m; ++i) 
			ans1 += a[i];
		
		for(int i = n - 2 * m + 1;i <= n - m; ++i) 
			ans1 += a[i]/a[i + m];
		
		
		for(int i = m;i <= n - m; ++i) 
			ans2 += a[i];
		
		for(int i = 1;i <= m; ++i) 
			ans2 += a[i]/a[n - m + i - 1];
		
		printf("%lld\\n",min(ans1,ans2));
 	
	
	
	return 0;

E. Singers’ Tour(消元+初中数学)

题意

给你一个长度为n的数组a，$a_i$表示第$i$个环形城市(即n个城市过了就是第一个城市)的音乐时常，然后每一个城市都有一个音乐家，他在本城市的的音乐时常为$b_i$，在下一个城市的时长为$2\ast b_i$……一直到后面n个城市为$n\ast b_i$，每个城市的$a_i$也就是每个音乐家在这个城市的音乐时长和，构造一个满足条件的b数组

思路

很显然这是一个n元一次方程，我们稍微化简一下就能做出来了

我们很轻松的可以列出下列方程(假设元素为4)

• $a_1=b[1]+4b[2]+3b[3]+2b[4]$

• $a_2=2b[1]+b[2]+4b[3]+3b[4]$

• $a_3=3b[1]+2b[2]+b[3]+4b[4]$

• $a_4=4b[1]+3b[2]+2b[3]+b[4]$

• $a_1=b[1]+4b[2]+3b[3]+2b[4]$

(要理解这里的a1其实就是想表示环形)

我们将两个相邻的相减即可得到(例如我们将$a_2-a_1$)：

$a_2-a_1=b[1]-3b[2]+b[3]+b[4]$

设一个$sum={\sum }_{i=1}^{n}b[i]$

上式可转化为：

$b[1]+b[2]+b[3]+$

Codeforces Round #393 div2

Codeforces Round #436 E. Fire（背包dp+输出路径）

[ACM]Codeforces Round #534 (Div. 2)

Codeforces Round #393 (Div. 2) (8VC Venture Cup 2017 - Final Round Div. 2 Edition) E - Nikita and st

Codeforces Round #726 (Div. 2) B. Bad Boy(贪心)