Codeforces Round #760 (Div. 3) (ABCDEF)

Posted 2022-01-06 斗奋力努

Codeforces Round #760 (Div. 3)

题目
A. Polycarp and Sums of Subsequences
题意：t组样例，每组样例输入从小到大输入7个数构成b数组，问b数组中是否存在三个数，通过给出的方法可以得到b数组。

思路：t的范围5000，同时每组样例才7个数，我们直接暴力枚举每次选的那三个元素就行，最后去跟b数组比较看是否相同。

#include<bits/stdc++.h>
using namespace std;
int a[10],b[10];

bool cek()
    sort(b+1,b+8);
    for(int i=1;i<=7;i++)
        if(a[i]==b[i]) continue;
        return false;
    
    return true;


void solve()
    for(int i=1;i<=7;i++) scanf("%d",&a[i]);
    for(int i=1;i<=7;i++)
        for(int j=i+1;j<=7;j++)
            for(int k=j+1;k<=7;k++)
                int cnt=0;
                b[++cnt]=a[i];
                b[++cnt]=a[j];
                b[++cnt]=a[k];
                b[++cnt]=a[i]+a[j];
                b[++cnt]=a[i]+a[k];
                b[++cnt]=a[j]+a[k];
                b[++cnt]=a[i]+a[j]+a[k];
                if(cek())printf("%d %d %d\\n",a[i],a[j],a[k]);return;
            
        
    


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

B. Missing Bigram
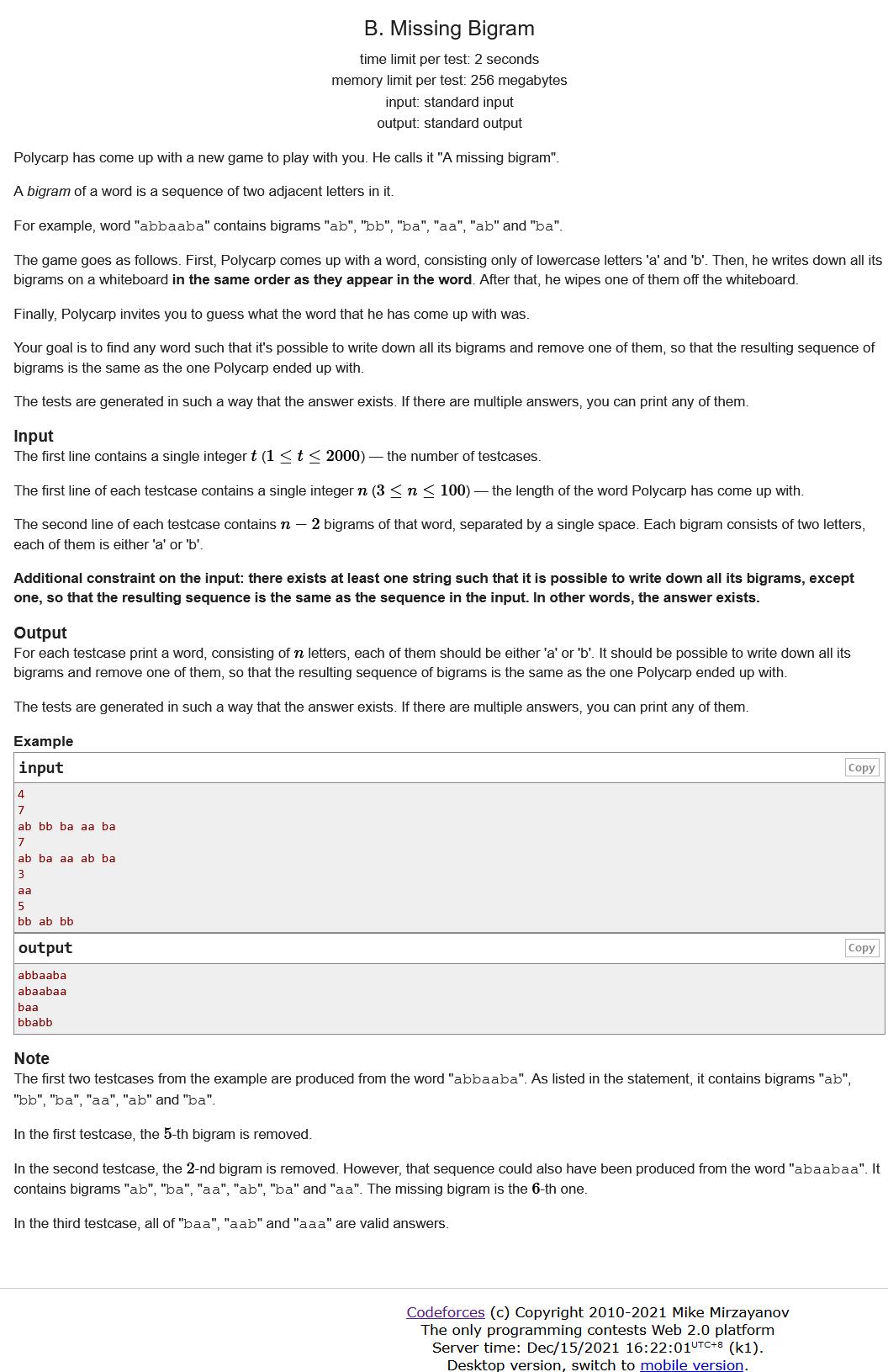题意：一个单词的二元组是其中两个相邻字母的序列，给了$n-2$个二元组，要求你构造一个长度为n的只包含${}^{\prime }{a}^{\prime }$和’${}^{\prime }{b}^{\prime }$的字符串s，s的所有二元组中随便删除一个，使得剩下的二元组等于给出的$n-2$个二元组
思路:
思路：直接以第一个二元组为前缀，之后在每次读入二元组的时候，判断一下当前的字符串s的末尾是否为读入二元组的第一个字符，不同则加入第一个字符，flag标记一下(这个就是删掉的那个)。随后可以就直接“拼接”起来(加上二元组的第二个字符)；最后flag要是没有标记，就随便加一个${}^{\prime }{a}^{\prime }$或$’b^{\prime }$就行了

#include<bits/stdc++.h>
using namespace std;
int n;

void solve()
    string ans;
    bool flag=false;
    cin>>n>>ans;
    for(int i=2;i<=n-2;i++)
        string ss; cin>>ss;
        if(ans[ans.length()-1]!=ss[0])
            ans.push_back(ss[0]);
            flag=true;
        
        ans.push_back(ss[1]);
    
    if(!flag) ans+="a";
    cout<<ans<<"\\n";


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

C. Paint the Array
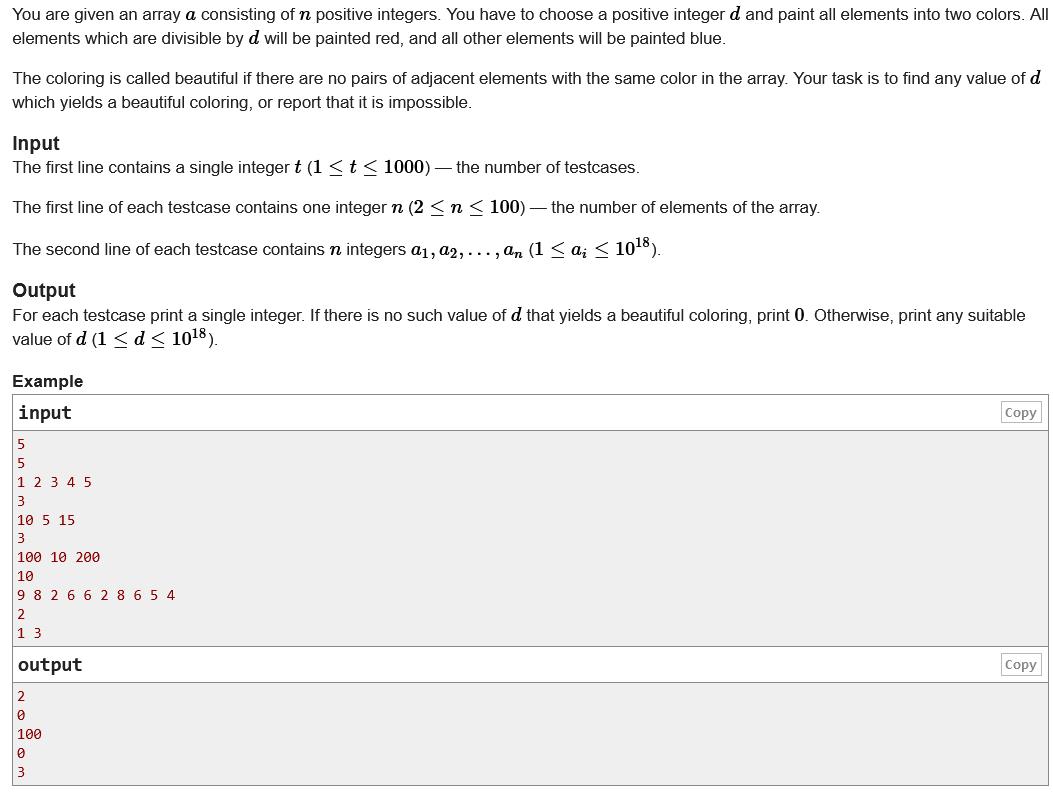题意：t组样例。每个样例给一个包含n个元素的序列，问是否存在一个数d，满足相邻的元素为满足下列两种形式之一，可以输出d，不可以输出0

形式1: (a1%d==0,a2%d!=0,a3%d==0,a4%d!=0....a(2x+1)%d==0,a(2x+2)%d!=0)
			即：
			if(i%2==1) ai%d==0;
			else if(i%2==0) ai%d!=0;
			
形式2: (a1%d!=0,a2%d==0,a3%d!=0,a4%d==0....a(2x+1)%d!=0,a(2x+2)%d==0)
			即：
			if(i%2==1) ai%d!=0;
			else if(i%2==0) ai%d==0;
			

思路：
开始想了一下质因数分解，感觉div3C题不至于这么搞，看了眼数据范围，发现果然不太行
发现对于第i个位置的元素，需要跟直接相邻的元素要没得关系，但跟位置i%2相同的所有元素有关，于是想到了对位置奇偶，然后分别求出奇偶位置所有元素的gcd值，对于得到的两个gcd值去暴力判断一下是否符合条件就行了，都不满足就输出0。
求gcd是因为这样可以保证所有i%2相同的元素去%gcd是等于0，即其中一种状态。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=105;
ll n,a[N],b[N];

bool cek(ll d)
    for(ll i=1;i<=n;i++)
        if(a[i]%d==0) b[i]=-1;
        else b[i]=1;
    
    for(ll i=2;i<=n;i++)
        if(b[i]!=b[i-1]) continue;
        return false;
    
    return true;


void solve()
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
    ll gcd1=a[1],gcd2=a[2];
    for(ll i=3;i<=n;i++)
        if(i%2==1) gcd1=__gcd(gcd1,a[i]);
        else gcd2=__gcd(gcd2,a[i]);
    
    if(cek(gcd1)) printf("%lld\\n",gcd1);
    else if(cek(gcd2)) printf("%lld\\n",gcd2);
    else puts("0");


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

D. Array and Operations
题意：t组样例，每组样例第一行读入两个数字n、k，代表给你一个包含n个元素的序列，要进行k次删除操作，每次操作删除两个数$ai,aj(i!=j)$，同时会得到一个分数$score=min(ai/aj,aj/ai)$，总分sum为剩下的$(n-2k)$个元素和加上每次删除操作得到的分数。
思路：贪心，将a数组从小到大排序后，规定剩下来的一定是最小的那$(n-2k)$个数，删除的是大的那$2k$个数，删除策略为每次删除中间间隔$k-1$个元素的两个元素，即分子为$a[i]$，分母为$a[i+k]$，这样计算出来的总分最小。(口胡的)

#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n,k,a[N],sum;

void solve()
    sum=0;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    sort(a+1,a+n+1);
    for(int i=1;i<=n-2*k;i++) sum+=a[i];
    for(int i=n-2*k+1,ci=1;ci<=k;ci++,i++) sum+=(a[i]/a[i+k]);
    printf("%d\\n",sum);


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

E. Singers’ Tour

题意：t组样例，每组样例给定一个包含n个元素的b数组,问是否可以构造出一个长度为n的a数组，满足a数组(环)中每个元素在到达$i$位置时的元素和等于$b[i]$。

对于元素$a[i]$

到达位置j	对位置j的贡献
j=i	a[i]
j=i+1	2*a[i]
j=i+2	3*a[i]
…	…
j=(i+k)%n+1	(k+2)⋅a[i]
j=(i+n−2)%n+1	n⋅a[i]

思路:这个肯定b数组的$sum$要是$(1+n)\ast n/2$的倍数，因为要求$1\le a[i]\le 10^9$，所以在任何情况在都应该会满足$sum\%((1+n)\ast n/2)==0$。同时我们会发现这是一个n元一次方程，剩下的就是解方程组就行了(本题高斯消元肯定不行)

/*
n=3， b[1] b[2] b[3]

b[1]=a[1]+3*a[2]+2*a[3]  ①式
b[2]=2*a[1]+a[2]+3*a[3]  ②式

由①-②得：
b[1]-b[2]=-a[1]+2*a[2]-a[3]  ③式

③式等价变换：
2*a[2]=b[1]-b[2]+a[1]+a[3]  ④式

④式左右两边同时加a[2]
3*a[2]=b[1]-b[2]+(a[1]+a[2]+a[3])   ⑤式 
(di=a[1]+a[2]+a[3])

⑤式等价变换：
n*a[2]=b[1]-b[2]+di  ⑥式

⑥式等价变换：
a[2]=(b[1]-b[2]+di)/n
(a[i]=(b[(i-1+n)%n]-b[i]+di))/n

*/

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=4e4+5;
ll n,b[N],t[N],sum;

void solve()
    sum=0;
    scanf("%lld",&n);
    for(ll i=0;i<n;i++)
        scanf("%lld",&b[i]);
        sum+=b[i];
    
    ll di=(1+n)*n
以上是关于Codeforces Round #760 (Div. 3) (ABCDEF)的主要内容，如果未能解决你的问题，请参考以下文章
 
 Codeforces Round #760 (Div. 3)
 Codeforces Round #393 div2
 Codeforces Round #436 E. Fire（背包dp+输出路径）
 [ACM]Codeforces Round #534 (Div. 2)
 Codeforces Round #393 (Div. 2) (8VC Venture Cup 2017 - Final Round Div. 2 Edition) E - Nikita and st
 Codeforces Round #726 (Div. 2) B. Bad Boy(贪心)