机器学习Python详细实现基于欧式Euclidean切比雪夫Chebyshew曼哈顿Manhattan距离的Kmeans聚类

Posted 2022-01-06 Better Bench

目录

• 1 算法过程
• 2 实现
• • 2.1 Python代码
  • 2.2 实验结果

1 算法过程

（1）随机选取K个簇中心点

（2）通过计算每个样本与每个簇中心点的距离，选择距离最小的簇心，将样本归类到该簇心的簇中
$$min\sum _{i=1}^K\sum _{x\in c_i}dist(c_i,x{)}^2$$

这里距离可以使用欧几里得距离（Euclidean Distance）、余弦距离（Cosine Distance）、切比雪夫距离（Chebyshew Distance）或曼哈顿距离（Manhattan Distance），计算距离之前需要先对特征值进行标准化。

3、在已经初次分配的簇中，计算该簇中所有向量的均值，作为该的簇中心点

4、重复步骤2和3来进行一定数量的迭代，直到簇中心点在迭代之间变化不大

评价指标

轮廓系数（Silhouette Coefficient），是聚类效果好坏的一种评价方式。 轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优。

2 实现

2.1 Python代码

# kmeans算法
#  1. 初始化k个族中心
#  2. 计算每个样本与k个族中心距离，标记样本为距离最短的族
#  3. 重新确定K族中心(族中平均位置)
#  4. 循环2-3，直到前后两次所有族中心距离变化<eps
"""
# 输入：
    X: 2d数组, 形如(n_samples, m_features)，n_samples表示样本数，m_features表示特征维数
    K: int, 超参数，指定族格式
    metric：str, 距离类型，默认为欧式距离'Euler',其他暂时为实现
    eps: float, 精度（当族中心位置更新变化<eps时停止)
    random_state: 随机种子    
# 输出：
    centers: K族中心向量, 2d数组, 形如(K, m_features)
    pred: 1-d数组,长度为n_samples 
"""

import numpy as np
import random   # 用python的random模块，不用numpy的random
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from scipy.spatial.distance import pdist
from sklearn.preprocessing import StandardScaler

class kmeans:  # 创建kmeans类

    # 初始化函数
    def __init__(self, X=None, K=2, metric='Euler',eps=1e-6, init_centers=None, random_state=None):
        self.X = X
        self.K = K
        self.metric = metric
        self.eps = eps
        self.centers = init_centers
        self.random_state = random_state


    # 距离函数
    def calc_dist(self, x, c):
        dist_list = []
        for i in range(c.shape[0]):
            v = c[i]
            # 欧式距离
            if self.metric == 'Euler':
                lp = 2
                distance = np.power(np.power(x-v, lp), 1/lp).sum()
                dist_list.append(distance)
            # 切比雪夫距离
            elif self.metric == 'Chebyshew':
                distance = abs((x)-v).max()
                dist_list.append(distance)
            # 曼哈顿距离
            elif self.metric == 'Manhattan':
                distance = sum(abs(x-v))
                dist_list.append(distance)
            # jaccard距离
            elif self.metric == 'Jaccard':
                matV = np.vstack([x, v])
                distance = pdist(matV, 'jaccard')
                dist_list.append(distance)
            # 余弦距离
            elif self.metric == 'Cosine':
                distance = np.dot(x, v) /(np.linalg.norm(x)*np.linalg.norm(v))
                dist_list.append(distance)
        return dist_list

    # 迭代(训练)
    def fit(self, X):
        # 样本
        if X is not None:
            self.X = X
        # 样本形状
        n_samples, n_features = self.X.shape

        # 设置随机种子
        if self.random_state is not None:
            random.seed(self.random_state)

        # 初始化聚类中心
        if self.centers is None:
            # 随机选取簇心（这点可改进，比如kmeans++就是在此改进的）
            idx = idx = random.sample(range(n_samples), self.K)
            self.centers = X[idx, :]

        # 初始样本的族标记-1
        pred = np.array([-1]*n_samples)

        iter = 0
        stop = False  # 结束标志
        while (not stop):
            iter += 1
            print(iter)
            for i in range(n_samples):
                dists = self.calc_dist(X[i, :], self.centers)
                pred[i] = np.argmin(dists)

            # 重新确定族中心
            new_centers = np.zeros((self.K, n_features))
            for k in range(self.K):
                new_centers[k, :] = X[pred == k, :].mean(axis=0)

            # 判断停止条件
            delta = abs(new_centers - self.centers)
            flg = delta < self.eps
            stop = flg.all()
            self.centers = new_centers

        return pred, self.centers

    # 族预测
    def predict(self, X):
        # 遍历所有样本，划分族
        pred = np.array([-1]*n_samples)
        for i in range(n_samples):
            dists = self.calc_dist(X[i, :], self.centers)
            pred[i] = np.argmin(dists)
        return pred


if __name__ == "__main__":


    # 生成数据
    n_samples = 1500
    random_state = 170
    X, y = make_blobs(n_samples=n_samples, random_state=random_state)

    # 调用kmeans
    metric_dist = 'Cosine'
    model = kmeans(X, K=3, metric=metric_dist, eps=1e-3, random_state=1)

    ss = StandardScaler()
    X_n = ss.fit_transform(X)
    pred, centers = model.fit(X_n)
    n_samples, _ = X.shape
    # 评价指标：轮廓系数，【-1 1】越接近1 ，聚类效果越好
    score = silhouette_score(X, pred)

    # 族预测，如果仅是训练数据，直接用fit(X)返回的族划分
    # pred = model.predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=pred)
    plt.title("—kmeans".format(metric_dist))
    plt.show()
    print()

2.2 实验结果

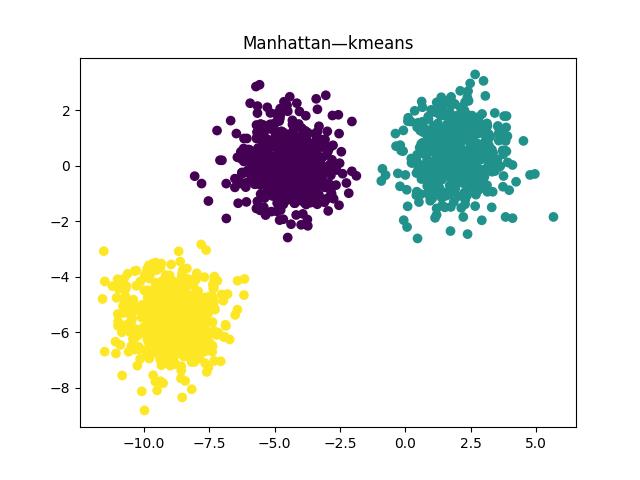
（1）曼哈顿距离

轮廓系数：0.7333423486262539

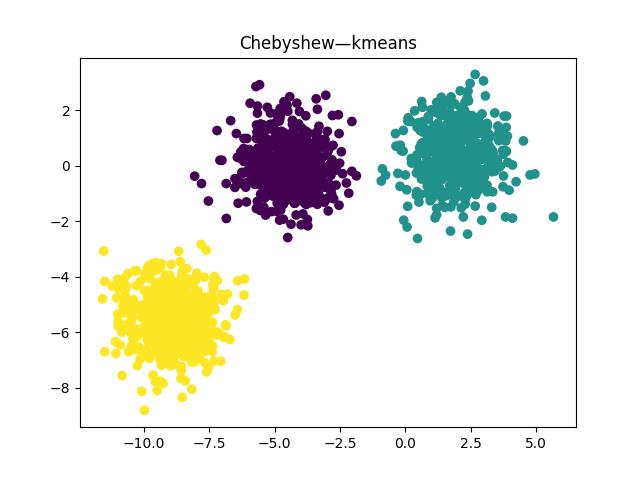
（2）切比雪夫距离

轮廓系数0.7333423486262539

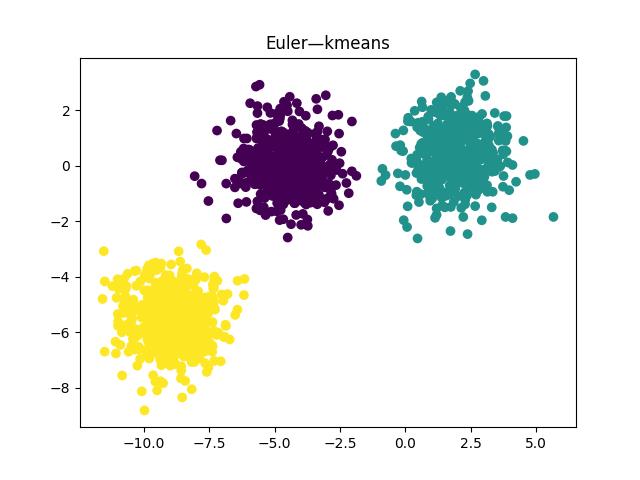
（3）欧式距离

轮廓系数：0.7333423486262539