转载深度学习-卷积神经网络（CNN）

Posted 2022-01-06 AXYZdong

1. CNN基本原理
2. 经典CNN

卷积神经网络基本原理

卷积神经网络的基本结构大致包括：卷积层、激活函数、池化层、全连接层、输出层等。

卷积层

二维卷积运算：给定二维的图像I作为输入，二维卷积核K，卷积运算可表示为 $S(i,j)=(I\ast K)(i,j)=\sum m\sum nI(i-m,j-n)K(m,n)$，卷积核需要进行上下翻转和左右反转

$$S(i,j)=\sum \left(\begin{array}{c}\left[\begin{array}{ccc}I(i-2,j-2)& I(i-2,j-1)& I(i-2,j)\\ I(i-1,j-2)& I(i-1,j-1)& I(i-1,j)\\ I(i,j-2)& I(i,j-1)& I(i,j)\end{array}\right]\left[\begin{array}{ccc}K(2,2)& K(2,1)& K(2,0)\\ K(1,2)& K(1,1)& K(1,0)\\ K(0,2)& K(0,1)& K(0,0)\end{array}\right]\end{array}\right)$$

卷积实际上就是互相关

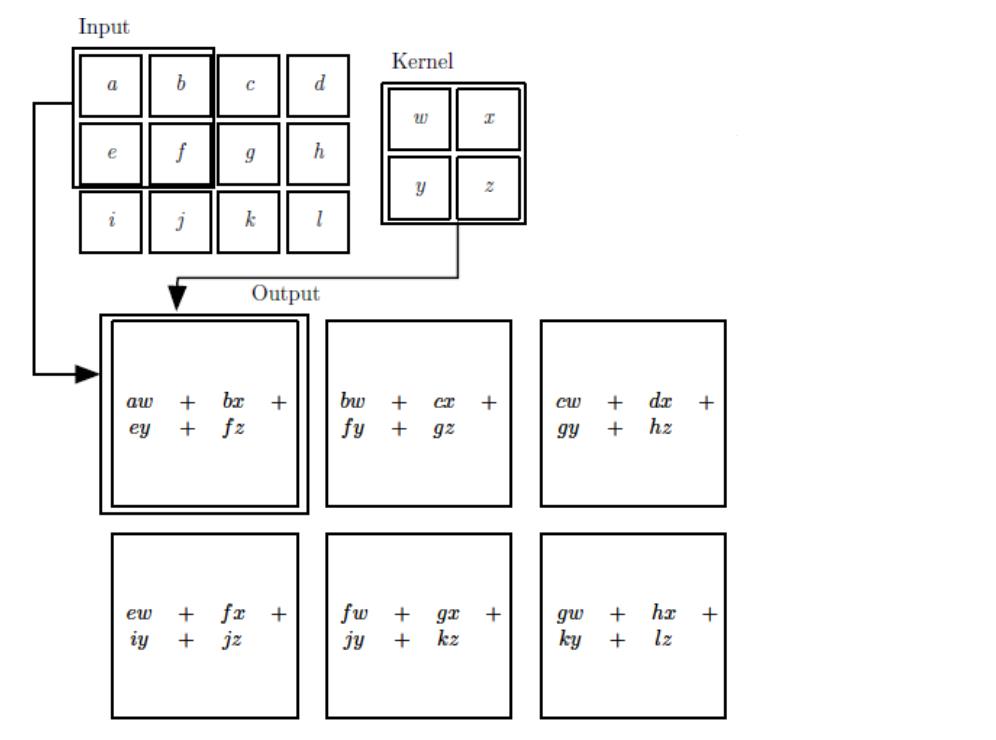
卷积的步长(stride)：卷积核移动的步长

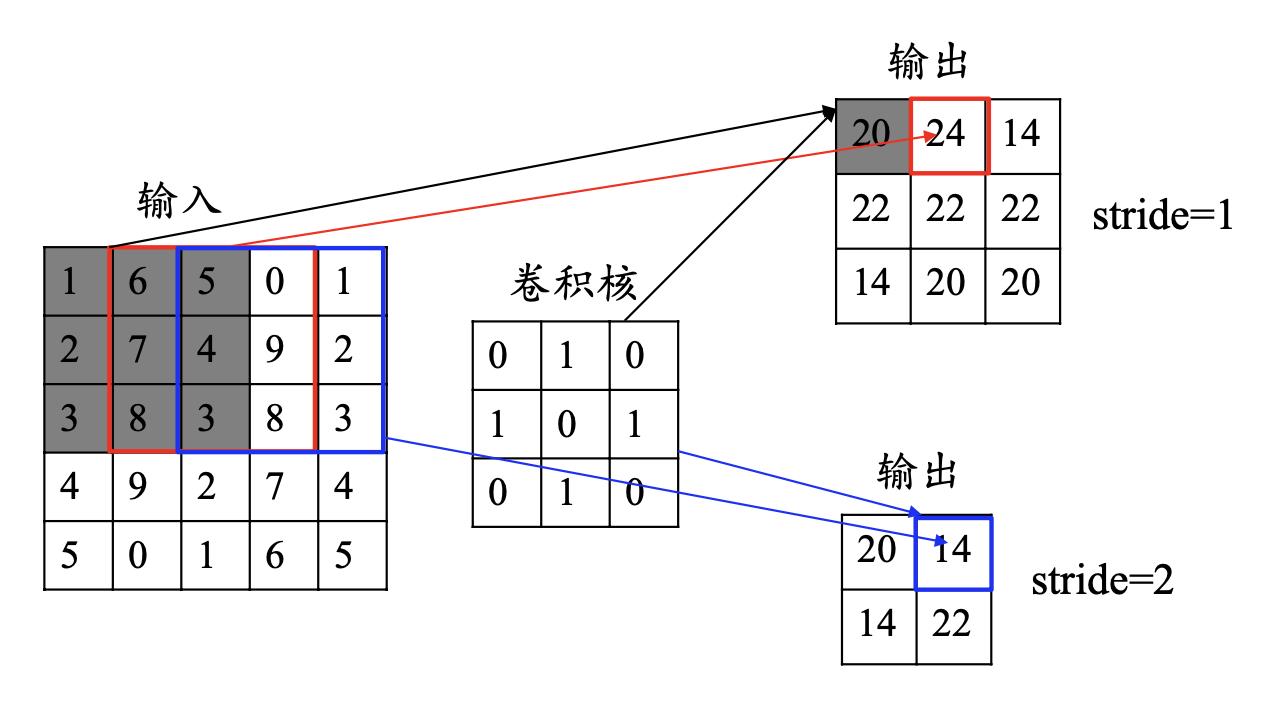
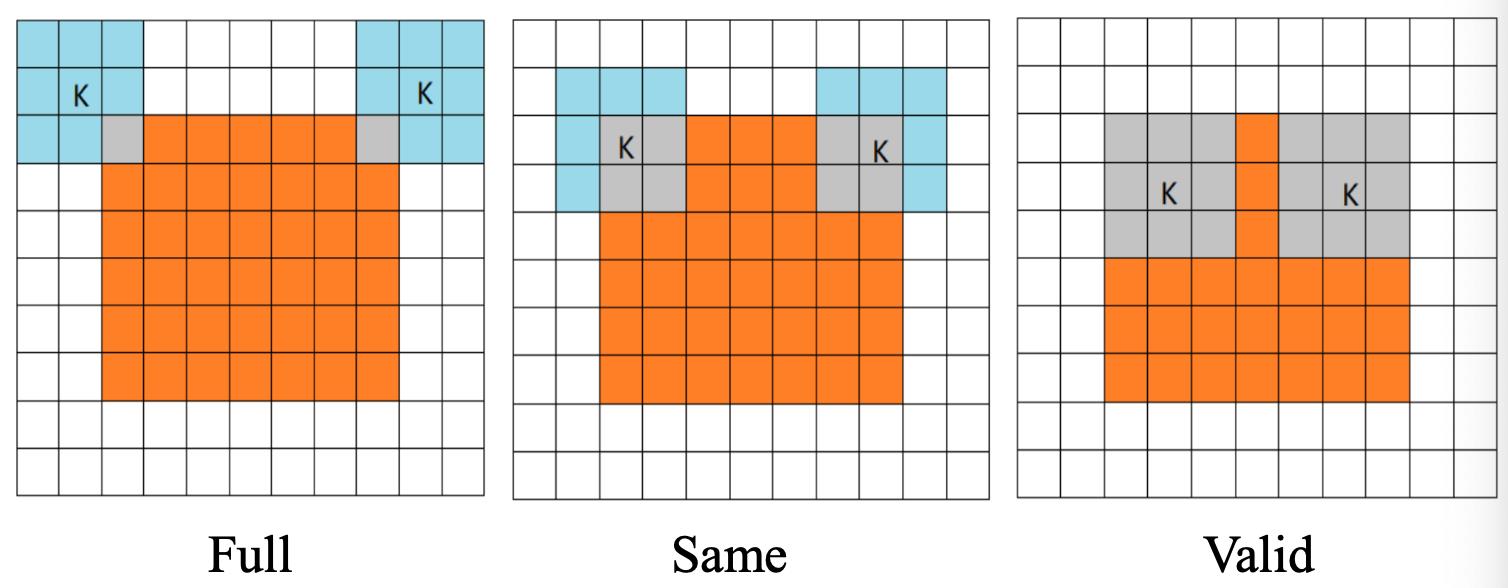
卷积的模式：Full**,** Same和Valid

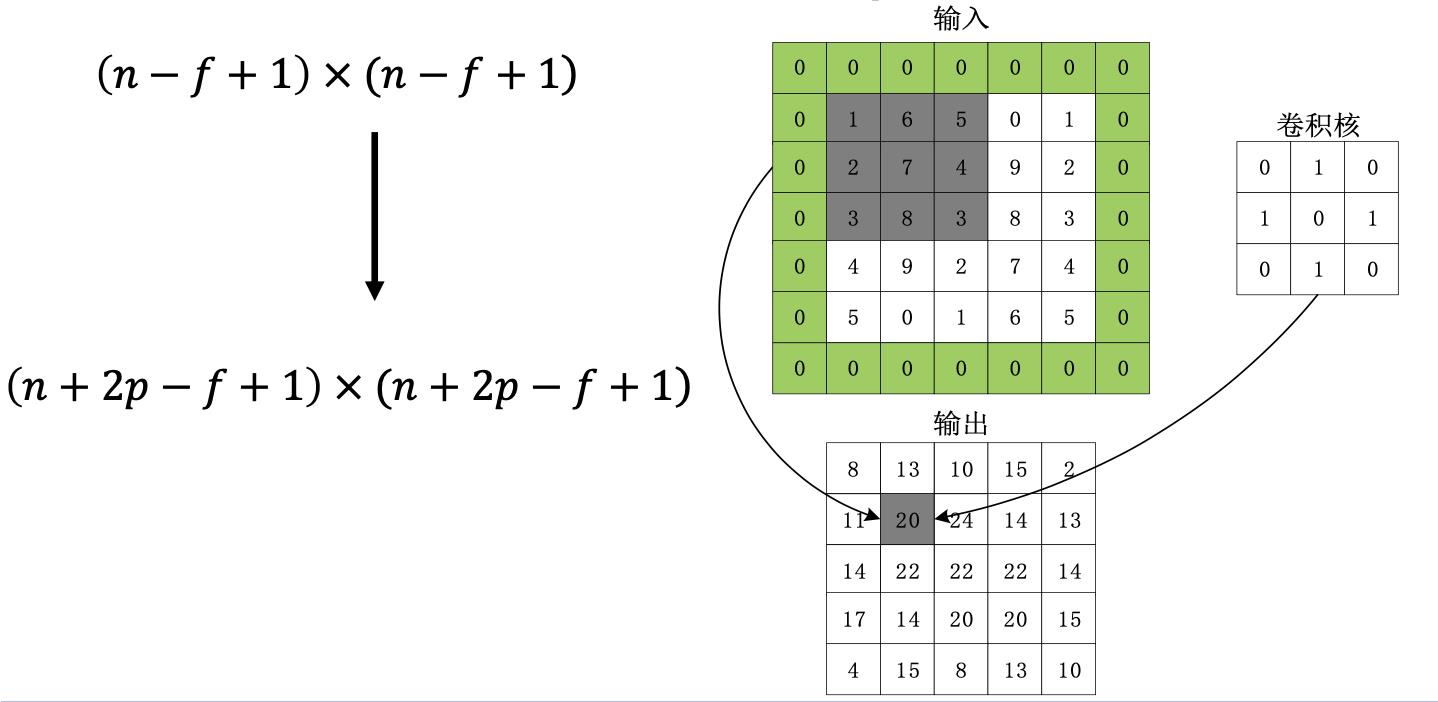
数据填充：如果我们有一个 𝑛×𝑛 的图像，使用𝑓×𝑓 的卷积核进行卷积操作，在进行卷积操作之前我们在图像周围填充 𝑝 层数据，输出的维度：

感受野：卷积神经网络每一层输出的特征图(featuremap)上的像素点在输 入图片上映射的区域大小，即特征图上的一个点对应输入图上的区 域。

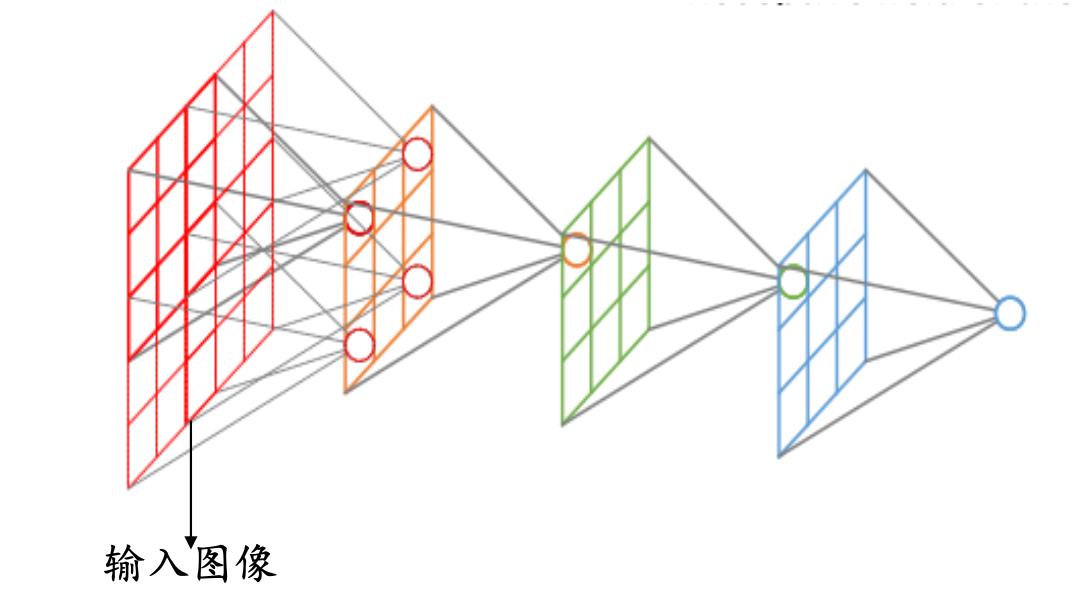
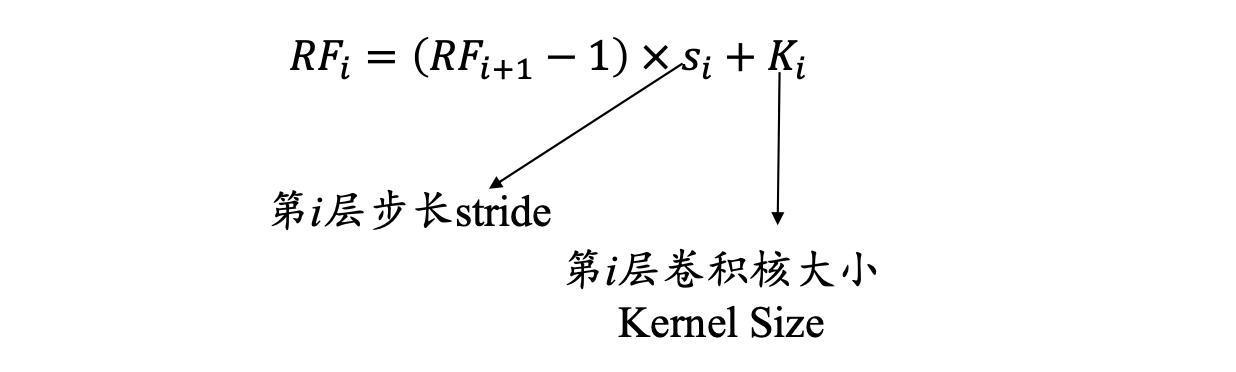
那么如何计算感受野的大小，可以采用从后往前逐层的计算方法：

• 第 i 层的感受野大小和第 *i-*1 层的卷积核大小和步长有关系，同时也与第 (*i-*1)层感受野大小有关
• 假设最后一层(卷积层或池化层)输出特征图感受野的大小(相对于其直 接输入而言)等于卷积核的大小

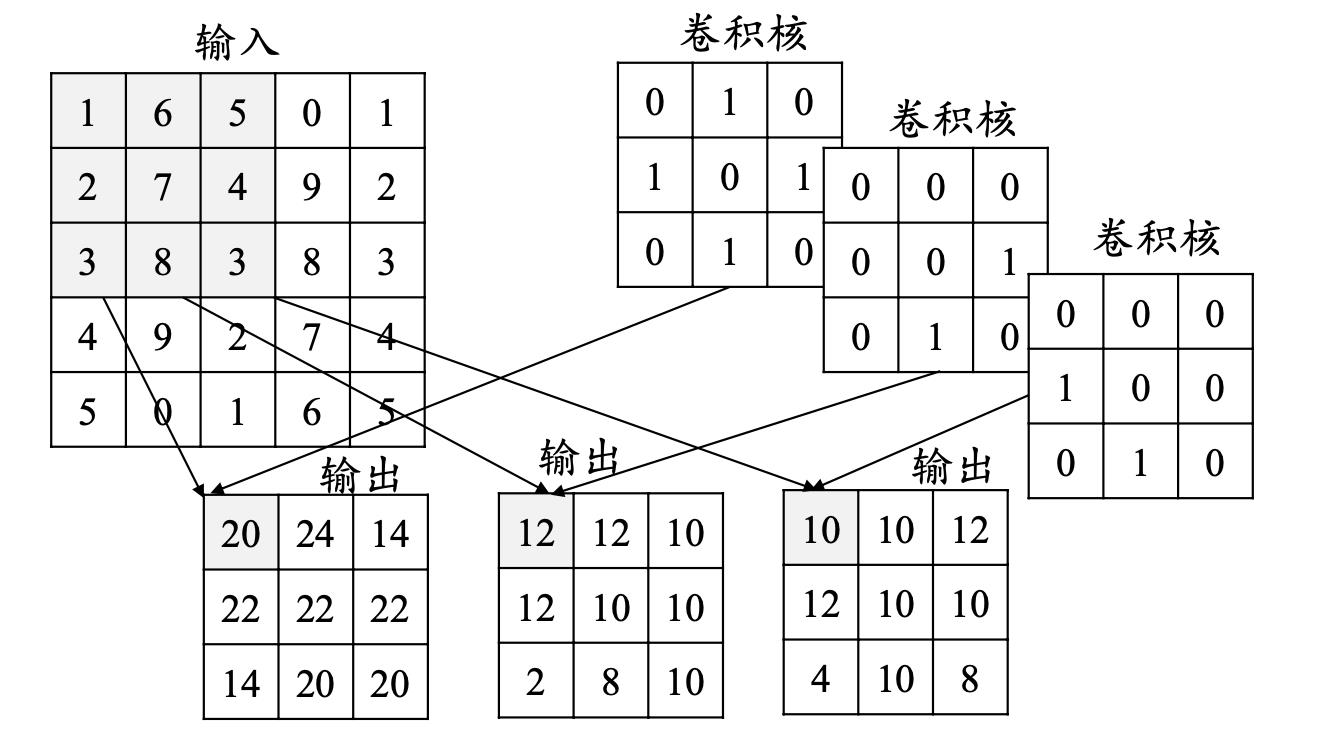
卷积层的深度(卷积核个数)：一个卷积层通常包含多个尺寸一致的卷积核

【卷积核的大小一般为奇数奇数】 11，33，55，77都是最常见的。这是为什么呢？为什么没有偶数偶数？

（1）更容易padding

在卷积时，我们有时候需要卷积前后的尺寸不变。这时候我们就需要用到padding。假设图像的大小，也就是被卷积对象的大小为nn，卷积核大小为kk，padding的幅度设为(k-1)/2时，卷积后的输出就为(n-k+2*((k-1)/2))/1+1=n，即卷积输出为n*n，保证了卷积前后尺寸不变。但是如果k是偶数的话，(k-1)/2就不是整数了。

（2）更容易找到卷积锚点

在CNN中，进行卷积操作时一般会以卷积核模块的一个位置为基准进行滑动，这个基准通常就是卷积核模块的中心。若卷积核为奇数，卷积锚点很好找，自然就是卷积模块中心，但如果卷积核是偶数，这时候就没有办法确定了，让谁是锚点似乎都不怎么好。

激活函数

激活函数是用来加入非线性因素，提高网络表达能力，卷积神经网络中最常用的是ReLU，Sigmoid使用较少。

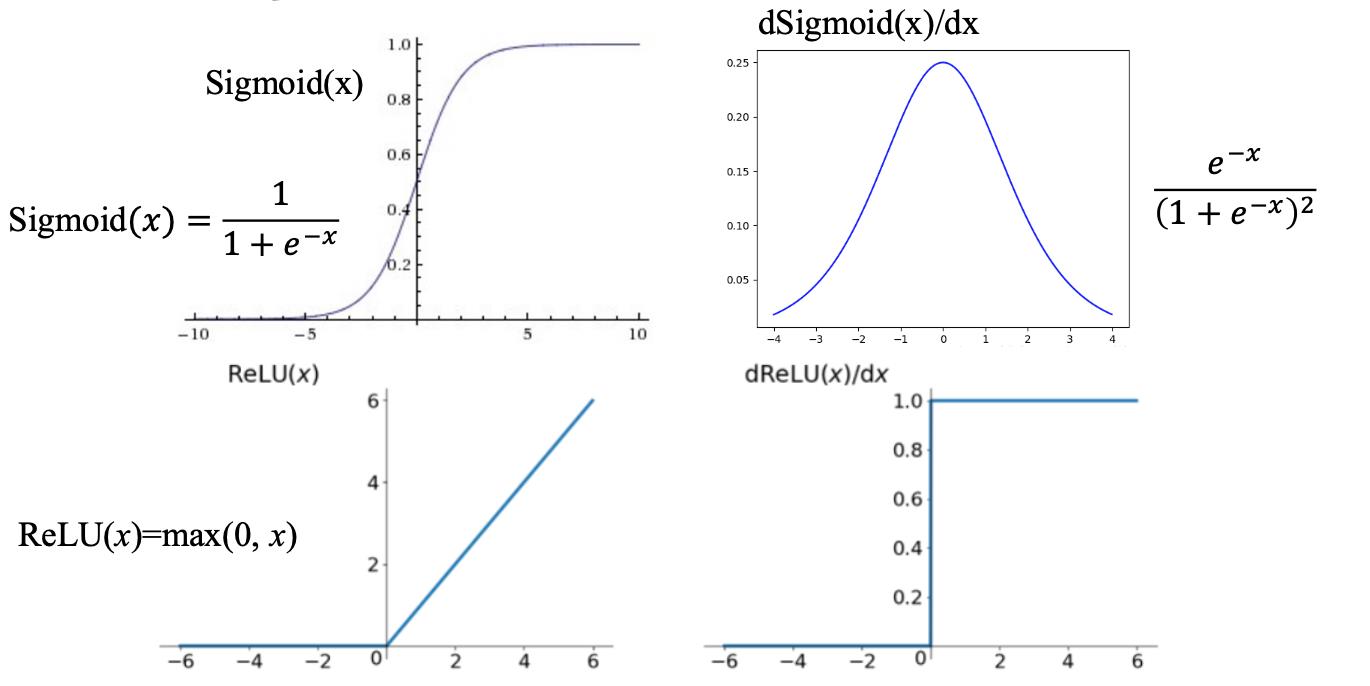
1. ReLU函数

$$f(x)=\{\begin{array}{l}0,x<0\\ x,x\ge 0\end{array}$$

ReLU函数的优点：

• 计算速度快，ReLU函数只有线性关系，比Sigmoid和Tanh要快很多
• 输入为正数的时候，不存在梯度消失问题

ReLU函数的缺点：

• 强制性把负值置为0，可能丢掉一些特征
• 当输入为负数时，权重无法更新，导致“神经元死亡”(学习率不 要太大)

2. Parametric ReLU

$$f(x)=\{\begin{array}{l}\alpha x,x<0\\ x,x\ge 0\end{array}$$

• 当 𝛼=0.01 时，称作Leaky ReLU
• 当 𝛼 从高斯分布中随机产生时，称为Randomized ReLU(RReLU)

PReLU函数的优点：

• 比sigmoid/tanh收敛快
• 解决了ReLU的“神经元死亡”问题

PReLU函数的缺点：需要再学习一个参数，工作量变大

3. ELU函数

$$f(x)=\{\begin{array}{l}\alpha (e^x-1),x<0\\ x,x\ge 0\end{array}$$

ELU函数的优点：

• 处理含有噪声的数据有优势
• 更容易收敛

ELU函数的缺点：计算量较大，收敛速度较慢

• CNN在卷积层尽量不要使用Sigmoid和Tanh，将导致梯度消失。
• 首先选用ReLU，使用较小的学习率，以免造成神经元死亡的情况。
• 如果ReLU失效，考虑使用Leaky ReLU、PReLU、ELU或者Maxout，此时一般情况都可以解决

特征图

• 浅层卷积层：提取的是图像基本特征，如边缘、方向和纹理等特征
• 深层卷积层：提取的是图像高阶特征，出现了高层语义模式，如“车轮”、“人脸”等特征

池化层

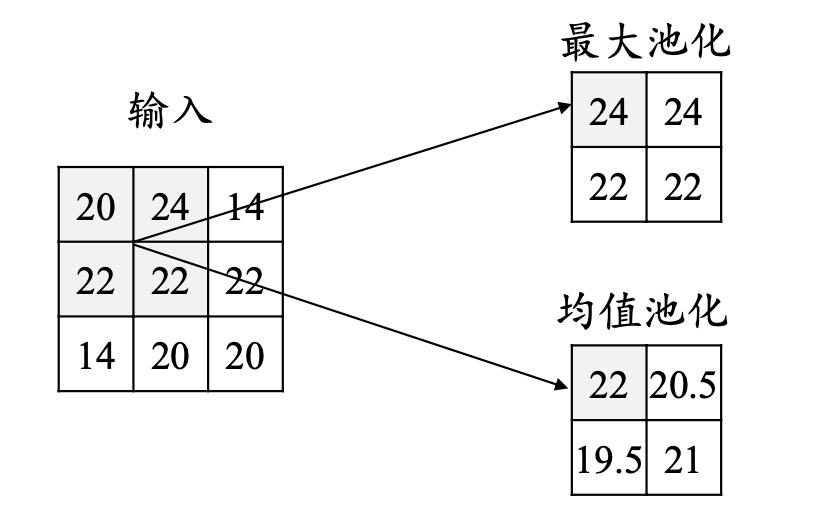
池化操作使用某位置相邻输出的总体统计特征作为该位置 的输出，常用最大池化(max-pooling)和均值池化(average- pooling)。

池化层不包含需要训练学习的参数，仅需指定池化操作的核大小、操作步幅以及池化类型。

池化的作用：

• 减少网络中的参数计算量，从而遏制过拟合
• 增强网络对输入图像中的小变形、扭曲、平移的鲁棒性(输入里的微 小扭曲不会改变池化输出——因为我们在局部邻域已经取了最大值/ 平均值)
• 帮助我们获得不因尺寸而改变的等效图片表征。这非常有用，因为 这样我们就可以探测到图片里的物体，不管它在哪个位置

全连接层

• 对卷积层和池化层输出的特征图(二维)进行降维
• 将学到的特征表示映射到样本标记空间的作用

输出层

对于分类问题：使用Softmax函数
$$y_i=\frac{e^{z_i}}{{\sum }_{i=1}^n{e}^{z_i}}$$

对于回归问题：使用线性函数
y i = ∑ m = 1 M w i m

以上是关于转载深度学习-卷积神经网络（CNN）的主要内容，如果未能解决你的问题，请参考以下文章

深度学习实战——卷积神经网络/CNN实践(LeNetResnet)

深度学习方法：卷积神经网络CNN经典模型整理Lenet，Alexnet，Googlenet，VGG，Deep Residual Learning

深度学习卷积神经网络(CNN)原理

深度学习算法实践10---卷积神经网络（CNN）原理

深度学习1-理解卷积神经网络（CNN)

对卷积神经网络(CNN)的理解——深度学习