SciPy 科学计算基础

Posted 2022-01-05 ZSYL

SciPy 科学计算基础

• SciPy科学计算基础
• • SciPy的constants模块
  • SciPy的special模块
  • SciPy.linalg
  • SciPy中的优化
  • SciPy中的图像处理
  • SciPy中的信号处理

SciPy科学计算基础

Scipy是一款用于数学、科学和工程领域的Python工具包，可以处理插值、积分、优化、图像处理、常微分方程数值解的求解、信号处理等问题。

SciPy的constants模块

SciPy的constants模块包含了大量用于科学计算的常数。

from scipy import constants as C

print(C.pi)   #圆周率
print(C.golden)   #黄金比例
print(C.c)   #真空中的光速
print(C.h)    #普朗克常数
print(C.mile)   #一英里等于多少米
print(C.inch)   #一英寸等于多少米
print(C.degree)   #一度等于多少弧度
print(C.minute)  #一分钟等于多少秒
print(C.g)   #标准重力加速度

SciPy的special模块

SciPy的special模块包含了大量函数库，包括基本数学函数、特殊函数以及NumPy中的所有函数。

from scipy import special as S

print(S.cbrt(8)) #立方根
print(S.exp10(3)) #10**3
print(S.sindg(90)) #正弦函数，参数为角度
print(S.round(3.1)) #四舍五入函数
print(S.round(3.5))
print(S.round(3.499))
print(S.comb(5,3))
#从5个中任选3个的组合数
print(S.perm(5,3)) #排列数
print(S.gamma(4)) #gamma函数
print(S.beta(10,200)) #beta函数
print(S.sinc(0)) #sinc函数

SciPy.linalg

SciPy.linalg是SciPy中实现线性代数计算的模块，常用的导入方式为：from scipy import linalg

在NumPy中，矩阵有矩阵类型和二维数组两种表示方法。

（1）数组类型下的基本操作

矩阵类型数据可以用np.mat()或mat.matrix()创建。

from scipy import linalg 
import numpy as np 

A = np.mat('[1,2;3,4]')
print('A矩阵为：\\n',A)
print('A的转置矩阵为：\\n',A.T)
print('A的逆矩阵为：\\n',A.I)

矩阵类型下的基本操作

矩阵也可以用二维数组对象表示，数组对象的矩阵操作与矩阵对象有一定的区别。

M = np.array([[1,2],[3,4]])
print('M矩阵为：\\n',M)
print('M的转置矩阵为：\\n',M.T)
print('M的逆矩阵为：\\n',linalg.inv(M))

线性方程组求解

除了通过矩阵的逆求解外可以直接使用linalg.solve()函数求解而且效率更高。

from scipy import linalg 
import numpy as np 
a = np.array([[1, 3, 5], [2, 5, -1], [2, 4, 7]])
b = np.array([10, 6, 4]) 
x = linalg.solve(a, b) 
print(x)

[-14.31578947   7.05263158   0.63157895]

行列式的计算

行列式是一个将方阵映射到标量的函数。linalg.det()可以计算矩阵的行列式。

M = np.array([[1,2],[3,4]])
linalg.det(M) 
-2.0

范数

范数是数学上一个类似“长度”的概念。linalg.norm()函数可以计算向量或矩阵的范数（或者模）。常见范数及其含义见下表。

M = np.array([[1,2],[3,4]])
print('M矩阵为：\\n',M)
print('M矩阵的L范数为：\\n',linalg.norm(M,1))  # 6.0
print('M矩阵的2范数为：\\n',linalg.norm(M,2))

特征值求解

函数linalg.eig()可以用来求解特征值和特征向量。

A = np.array([[1,2],[3,4]])
l,v = linalg.eig(A)
print(l)
print(v)

[-0.37228132+0.j  5.37228132+0.j]
[[-0.82456484 -0.41597356]
 [ 0.56576746 -0.90937671]]

奇异值分解

奇异值分解是一个能适用于任意的矩阵的一种分解的方法。

scikit-learn的PCA算法的背后真正的实现就是用的SVD。

from numpy import *
data = mat([[1,2,3],[4,5,6]])
U,sigma,VT = np.linalg.svd(data)
print('U: ',U)
print('SIGMA:',sigma)
print('VT:',VT)

SciPy中的优化

SciPy.optimize包提供了几种常用的优化算法，包括用来求有/无约束的多元标量函数最小值算法，最小二乘法，求有/无约束的单变量函数最小值算法，还有解各种复杂方程的算法。

方程求解及求极值

使用SciPy.optimize模块的root和fsolve函数进行数值求解线性及非线性方程求方程的根。

from scipy.optimize import root
def func(x):
   return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)   
# 0.3 估计初始值
print (sol)

使用fmin，fminbound可以求函数的极值:

import numpy as np
from matplotlib import pyplot as plt
from SciPy.optimize import fmin,fminbound  
def f(x):    
     return x**2+10*np.sin(x)+1
x = np.linspace(-10,10,num = 500)
min1 = fmin(f,3)  #求3附近的极小值
min2 = fmin(f,0)  #求0附近的极小值
min_global = fminbound(f,-10,10) 
#这个区域的最小值
print(min1)
print(min2)
print(min_global)
plt.plot(x,f(x))
plt.show()

数据拟合

（1）多项式拟合

import matplotlib.pyplot as plt

x = np.linspace(-5,5,20)
y = 3.5*x+2.1
y_noise = y+np.random.randn(20)*2
coeff = np.polyfit(x,y_noise,1)
plt.plot(x,y_noise,'x',x,coeff[0]*x+coeff[1])
plt.show()

最小二乘拟合

最小二乘拟合(Least Squares)是一种常用的数学优化技术，通过最小化误差的平方和在寻找一个与数据匹配的最佳函数。

要使用最小二乘优化，需要先定义误差函数：

def errf(p,x,y):
	return y-func(x,*p)

其中，p表示要估计的真实参数，x是函数的输入，y表示输入对应的数据值。最小二乘估计对应的函数为optimize.leastsq()，可以利用该函数和定义的误差函数，对真实参数进行最小二乘估计。

from scipy import optimize
def myfunc(x,a,b,w,t):
    return a*np.exp(-b*np.sin(w*x+t))
    
x = np.linspace(0,2*np.pi)
par = [3,2,1.25,np.pi/4]
y = myfunc(x,*par)
y_noise = y+0.8*np.random.randn(len(y))
def errf(p,x,y):
    return y-myfunc(x,*p)
c,rv = optimize.leastsq(errf,[1,1,1,1],args = (x,y_noise))
#c返回找到的最小二乘估计
plt.plot(x,y_noise,'x',x,y,x,myfunc(x,*c),':')
plt.legend(['data','actual','leastsq'])
plt.show()

曲线拟合

可以不定义误差函数，用函数optimize.curve_fit()直接对函数myfunc的参数直接进行拟合。

p,e = optimize.curve_fit(myfunc,x,y_noise)
print('p是对参数的估计值:\\n',p)
print('e是4个估计参数的协方差矩阵:\\n',e)

p是对参数的估计值:
 [3.28292536 1.90102739 1.2478838  0.78989363]
e是4个估计参数的协方差矩阵:
 [[ 0.17453746 -0.05248031  0.01959142 -0.06158022]
 [-0.05248031  0.01606779 -0.00572988  0.01801028]
 [ 0.01959142 -0.00572988  0.00271714 -0.00854062]
 [-0.06158022  0.01801028 -0.00854062  0.02707182]]

稀疏矩阵的存储

稀疏矩阵(Sparse Matrix)是只有少部分元素值是非零的矩阵。如果按照正常方式存储所有元素，则这些矩阵将占用巨大空间，因此，稀疏矩阵只保存非零值及对应的位置。

SciPy.sparse是SciPy中负责稀疏矩阵的模块。在SciPy中，根据存储方式的不同，可以将稀疏矩阵分为以下几类：

• bsr_matrix(Block Sparse Row matrix):分块存储，基于行
• coo_matrix(A sparse matrix in COOrdinate format):坐标形式存储（COO）
• csc_matrix(Compressed Sparse Column matrix):基于列的压缩存储（CSC）
• csr_matrix(Compressed Sparse Row matrix):基于行的压缩存储（CSR）
• dia_matrix(Sparse matrix with DIAgonal storage):对角线存储
• dok_matrix(Ditictionary Of Keys based sparse matrix):基于键值对的存储
• lil_matrix(Row-based linked list sparse matrix):基于行的链表存储

稀疏矩阵的运算

由于稀疏矩阵数据量大，一般不使用普通矩阵作为参数来构建，而是采用非零数据点及坐标的形式构建。

import numpy as np
from scipy import sparse
sparse.coo_matrix((2,3))  #创建空的稀疏矩阵
A = sparse.coo_matrix([[1,2,0],[0,1,0],[2,0,0]]) 
#将普通矩阵转为稀疏矩阵
print(A)
print(type(A))    #查看A的类型
print(type(A.tocsc())) #不同类型的稀疏矩阵可以相互转换
v = np.array([1,3,-3])
print(A*v) 

data = [1,2,3,4]
rows = [0,0,1,2]
cols = [0,1,2,2]
W = sparse.coo_matrix(data,(rows,cols))
print('稀疏矩阵W：\\n',W)
r,c,d = sparse.find(W)
#find()函数返回非零元素的行、列和具体数值
print('稀疏矩阵W非零值：\\n',r,c,d)  

稀疏矩阵W：
   (0, 0)	1
  (0, 1)	2
  (0, 2)	3
  (0, 3)	4
稀疏矩阵W非零值：
 [0 0 0 0] [0 1 2 3] [1 2 3 4]

SciPy中的图像处理

简单的介绍一下SciPy在图像处理方面的应用，如果专业做图像处理当然还是建议使用OpenCV。

1 图像平滑

图像平滑是指用于突出图像的宽大区域、低频成分、主干部分或抑制图像噪声和干扰高频成分，使图像亮度平缓渐变，减小突变梯度，改善图像质量的图像处理方法。

图像平滑的方法包括：插值方法，线性平滑方法，卷积法等。

ndimage.median_filter实现中值滤波。

import numpy as np
from scipy import ndimage
from scipy import misc
import matplotlib.pyplot as plt
%matplotlib inline
image = misc.ascent()
aa = plt.subplot(1,3,1)
plt.title("title")
plt.imshow(image)
plt.axis('off')
plt.subplot(1,3,2)
plt.title("medi_filter")
filter = ndimage.median_filter(image,size=10)

#使用SciPy的中值滤波处理图片
plt.imshow(filter)
plt.axis('off')
plt.subplot(1,3,3)
plt.title("gausfilter")
blurred_face = ndimage.gaussian_filter(image, sigma = 7)
#高斯滤波
plt.imshow(blurred_face)
plt.axis('off')

图像旋转和锐化

图像锐化就是补偿图像的轮廓，增强图像的边缘及灰度跳变的部分，使图像变得清晰。图像锐化处理的目的是为了使图像的边缘、轮廓线以及图像的细节变的清晰。经过平滑的图像变得模糊的根本原因是因为图像受到了平均或积分运算，因此可以对其进行逆运算（如微分运算）就可以使图像变的清晰。从频域来考虑，图像模糊的实质是因为其高频分量被衰减，因此可以用高通滤波器来使图像清晰。

image = misc.ascent() 
#显示全部图片
plt.subplot(131)
plt.title("title")
plt.imshow(image)
plt.axis('off')
plt.subplot(132)
rotate = ndimage.rotate(image,60)
plt.title("rotate")
plt.imshow(rotate)

plt.axis('off') #边缘检测
plt.subplot(133)
prewitt = ndimage.prewitt(image)
plt.title("prewitt")
plt.imshow(prewitt)
plt.axis('off')

SciPy中的信号处理

信号处理(signal processing)是指对信号进行提取、变换、分析、综合等处理，以便抽取出有用信息的过程。信号处理基本的内容有变换、滤波、调制、解调、检测以及谱分析和估计等。

Python中的scipy.signal模块专门用于信号处理。

1 数据重采样

重采样指将数据序列从一个频率转化为另一个频率进行处理的过程。将高频率数据转化为低频率数据为降采样，低频率转化为高频率为升采样。SciPy中的signal.resample() 函数可以将信号重采样成n个点。

2 信号的卷积

卷积是两个变量在某范围内相乘后求和的结果。一维卷积常用于序列模型，如自然语言处理领域。二维卷积常用于计算机视觉、图像处理领域。

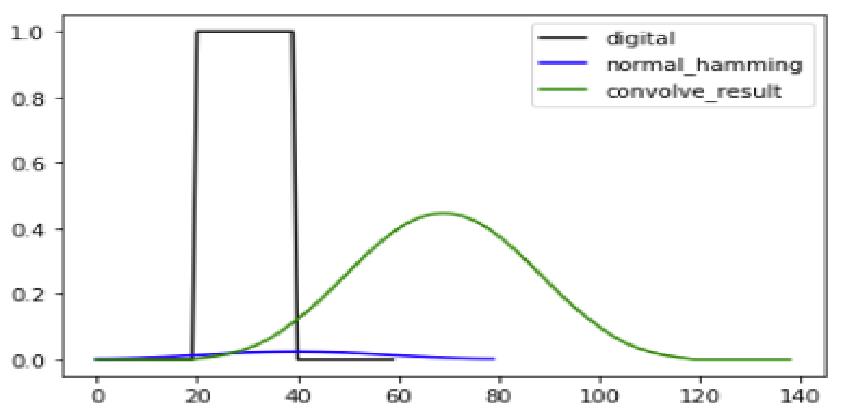
2 信号的卷积

卷积是两个变量在某范围内相乘后求和的结果。一维卷积常用于序列模型，如自然语言处理领域。二维卷积常用于计算机视觉、图像处理领域。

3 信号的时频分析

信号的表示是信息分析与处理的核心问题之一。在信号分析中，最基本的变量是时间和频率。

信号一般用时间作为自变量表示，通过时频变换，信号也可以使用频率作为自变量表示。常用的变换方法有傅里叶变换、小波变换等。

SciPy中利用fft方法将信号从时域变换到频率，用ifft方法将频域信号逆变换回时域。

---

加油!

感谢!

努力!