数据结构二叉树相关面试题 Java版 LeetCode题 ------- 二叉树
Posted wwzzzzzzzzzzzzz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构二叉树相关面试题 Java版 LeetCode题 ------- 二叉树相关的知识,希望对你有一定的参考价值。
文章目录
基础面试题
第一题: 二叉树的前序遍历。
LeetCode144: 二叉树的前序遍历
描述:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
(递归解法)
class Solution
public List<Integer> preorderTraversal(TreeNode root)
List<Integer> list = new ArrayList<>();
if(root == null) return list;
//访问根节点,将根节点加入list中
list.add(root.val);
//递归遍历左子树,把左子树的遍历结果加入到List中
list.addAll(preorderTraversal(root.left));
//递归遍历右子树,把右子树的遍历结果加入到List中
list.addAll(preorderTraversal(root.right));
return list;
(迭代解法)
思路:
- 迭代就是按照遍历的思路一步一步走.
- 用栈(Stack)来存入节点,按照: 根 -> 左 -> 右 的顺序存,
- 先入栈根节点,将根节点的值,插入到list中,再去入栈左节点
①如果左节点不为空,循环去入栈左节点,每次入栈时,将节点的值插入到list中,直到左节点为空,进入②操作
②如果左节点为空,就出栈获取栈顶元素的节点,然后访问该节点的右节点.循环 3.操作
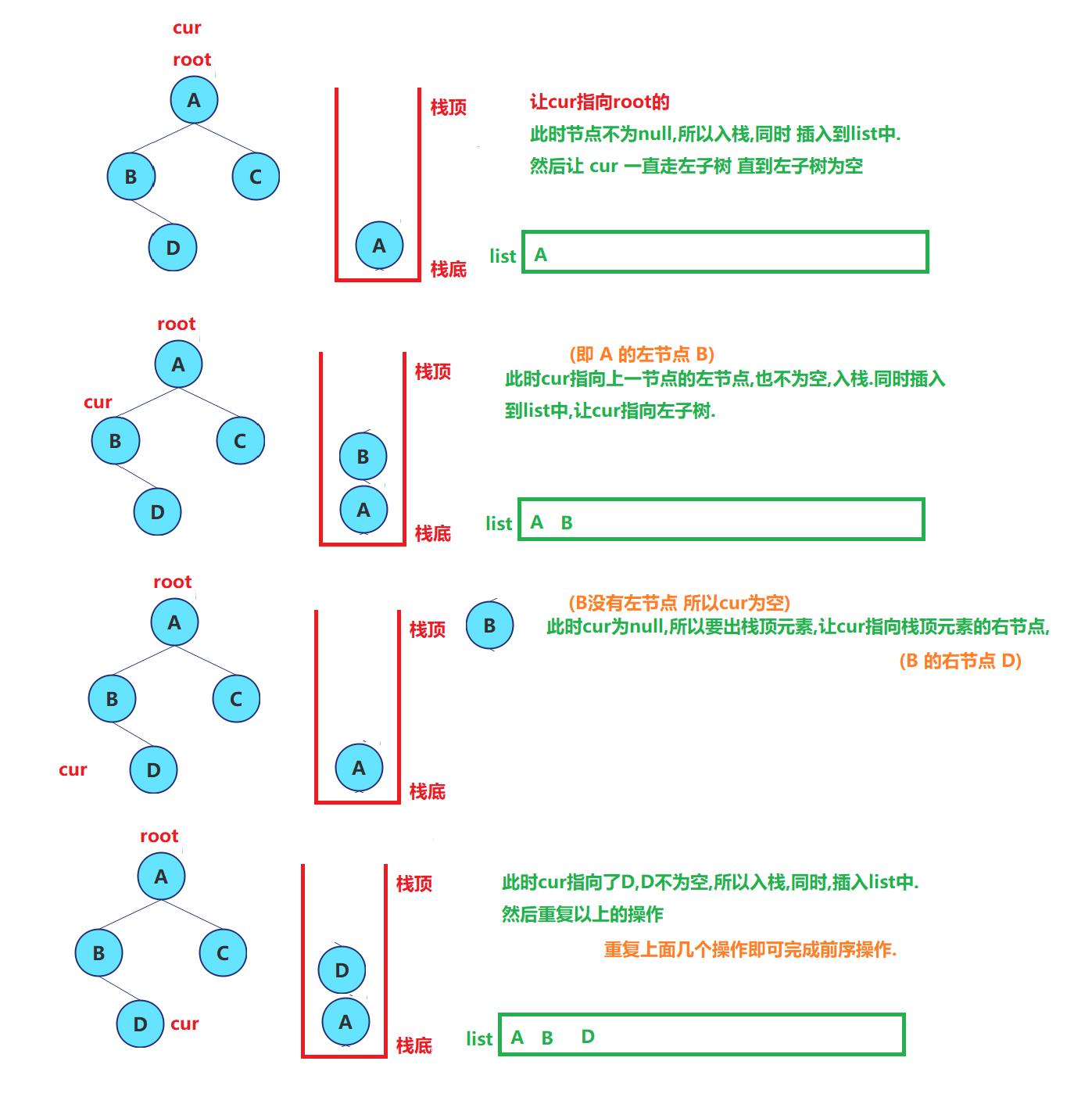
代码实现:
public List<Integer> preorderTraversal(TreeNode root)
List<Integer> list = new ArrayList<>();
if(root == null) return list;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
// 节点不为空 或者 栈不为空的时候进入循环
while(cur != null || !stack.empty())
// 节点不为空的时候入栈 同时插入list中然后让节点指向左节点.
while(cur != null)
stack.push(cur);
list.add(cur.val);
cur = cur.left;
//节点为空表示,没有左节点了,此时要弹出栈顶元素
TreeNode top = stack.pop();
//指向该节点的右节点,然后继续进行循环
cur = top.right;
return list;
第二题: 二叉树的中序遍历。
LeetCode 94: 二叉树的中序遍历
描述:
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
(递归解法)
class Solution
public List<Integer> inorderTraversal(TreeNode root)
List<Integer> list = new ArrayList<>();
if(root == null) return list;
//递归遍历左子树,把左子树的遍历结果加入到List中
list.addAll(inorderTraversal(root.left));
//访问根节点,将根节点加入list中
list.add(root.val);
//递归遍历右子树,把右子树的遍历结果加入到List中
list.addAll(inorderTraversal(root.right));
return list;
(迭代解法)
思路:
- 中序的迭代 和 前序的迭代差不多,只不过是插入list的时机不一样
- 这里的list插入是出栈的时候插入,因为栈顶肯定是先左子树,再父节点,然后右子树的. 相当于 左 -> 根 -> 右
public List<Integer> inorderTraversal(TreeNode root)
List<Integer> list = new ArrayList<>();
if (root == null) return list;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty())
while (cur != null)
stack.push(cur);
cur = cur.left;
TreeNode top = stack.pop();
list.add(top.val);//出栈的时候 插入list中
cur = top.right;
return list;
第三题: 二叉树的后序遍历。
LeetCode 145: 二叉树的后序遍历
描述:
给定一个二叉树,返回它的 后序 遍历。
(递归解法)
class Solution
public List<Integer> postorderTraversal(TreeNode root)
List<Integer> list = new ArrayList<>();
if(root == null) return list;
//递归遍历左子树,把左子树的遍历结果加入到List中
list.addAll(postorderTraversal(root.left));
//递归遍历右子树,把右子树的遍历结果加入到List中
list.addAll(postorderTraversal(root.right));
//访问根节点,将根节点加入list中
list.add(root.val);
return list;
(迭代解法)
思路:
- 相对于 前序 和 中序的 迭代,后序的迭代方法要更加难一点.
- 在循环将左子树入栈的时候,循环结束,不能直接出栈,要判断该左子树右节点是否还有节点,如果有节点要先将右节点插入到list中,如果没有右节点,表示该节点就是最左边的节点,直接出栈.
public List<Integer> postorderTraversal(TreeNode root)
List<Integer> list = new ArrayList<>();
if(root == null) return list;
TreeNode cur = root;
TreeNode pre = null;
Stack<TreeNode> stack = new Stack<>();
while(cur != null || !stack.empty())
while (cur != null)
stack.push(cur);
cur = cur.left;
//先判断栈顶元素是否还有右子树(因为是左->右->根,没有左节点了,还需要判断右节点.)
cur = stack.peek();
//如果没有右子树,或者右子树已经插入了,就继续出栈.
if(cur.right == null || cur.right == pre)
//该节点没有右子树了,出栈 插入到list中即可.
TreeNode topCur = stack.pop();
list.add(topCur.val);
pre = cur; //pre指向被插入的节点.用来判断是否插入过了
cur = null;
else
cur = cur.right;
return list;
第四题: 相同的树
LeetCode 100: 相同的树
描述:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
解题思路:
1. 如果两个二叉树都为空,则两个二叉树相同。
2. 如果两个二叉树中有且只有一个为空,则两个二叉树一定不相同。
3. 如果两个二叉树都不为空,那么首先判断它们的根节点的值是否相同, 若不相同,则两个二叉树一定不同, 若相同,再分别判断两个二叉树的左子树是否相同以及右子树是否相同。
4. 根据这3个条件,遍历两个二叉树的左子树和右子树是否相等.
代码实现:
class Solution
public boolean isSameTree(TreeNode p, TreeNode q)
//如果p q 节点同时为空 则相等
if(p == null && q == null) return true;
//1.如果p为空,q不为空 不相等
//2.如果p不为空,q为空 不相等
//3.p q都不为空,p的值 和 q的值 不相等
if(p == null || q== null || p.val != q.val) return false;
//递归左子树是否相等 和 右子树是否相等
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
第五题: 另一棵树的子树
LeetCode 572: 另一棵树的子树
描述:
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
解题思路:
1. 情况一 : 两个树 root 和 subRoot 是相同的
2. 情况二 : 左子树 root.left 和 subRoot 是相同的
3. 情况三 : 右子树 root.left 和 subRoot 是相同的
4. 不符合三种情况就是 subRoot 不是 root 的子树
5. 递归 为空 和 不符合情况 都是 false;比较相同用第四题的代码.
代码实现:
/**
* 判断是否是相同的树
**/
public boolean isSameTree(TreeNode p,TreeNode q)
if(p == null && q == null) return true;
if(p == null || q== null || p.val != q.val) return false;
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
public boolean isSubtree(TreeNode root, TreeNode subRoot)
// 递归遍历之后 为空 就是 flase;
if(root == null || subRoot == null) return false;
// 判断两个树是否相同
if(isSameTree(root,subRoot)) return true;
// 判断subRoot 是否是 root 的左子树
if(isSubtree(root.left,subRoot)) return true;
// 判断subRoot 是否是 root 的右子树
if(isSubtree(root.right,subRoot)) return true;
// 遍历结束还不相同 所以返回false;
return false;
第六题: 二叉树最大的深度
LeetCode 104: 二叉树最大的深度
描述:
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
解题思路:
1. 求出左子树的高度 leftHeight 和 右子树的高度 rightHeight.
2. 求出左子树和右子树的最大值
3. 求出最大值还需要+1
代码实现:
public int maxDepth(TreeNode root)
if(root == null)
return 0;
int leftHeight = maxDepth(root.left);// 左子树的深度
int rightHeight = maxDepth(root.right);// 右子树的深度
//求出最大值然后+1 就是树的最大深度
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
第七题: 判断一颗二叉树是否是平衡二叉树。
LeetCode 110: 平衡二叉树
描述:
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
方法一:自顶向下的递归—时间复杂度O(N^2)
1. 利用第六题的代码 可以求出任意节点的深度.
2. 自顶向下递归,每次判断当前节点的左右子树的高度差是否<=1,如果始终符合就是平衡二叉树,否则就是非平衡二叉树.
3. 然后递归的遍历这个节点的左节点 和 右节点,判断他们的左子树和右子树的差是否符合要求.
代码实现:
/**
* 求节点深度
**/
public int maxDepth(TreeNode root)
if(root == null)
return 0;
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
public boolean isBalanced(TreeNode root)
//节点为空的时候也符合条件 所有直接return true
if(root == null)
return true;
//求出左子树的深度 和 右子树的深度
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
//Math.abs()求出左右子树差的绝对值 如果<2就是true否则就是false
//isBalanced分别递归遍历节点的左节点和右节点的左右子树 是否符合题意
return Math.abs(leftHeight - rightHeight) < 2 && isBalanced(root.left) && isBalanced(root.right);
方法二: 自底向上的递归—时间复杂度O(N)
1. 对于当前遍历到的节点,先判断他的左右子树 是否平衡,再判断以当前节点为根的树是否平衡,
2. 如果子树是平衡的,返回子树的高度,
3. 如果子树不是平衡的,那么整个树都不会是平衡的,返回-1;
代码实现:
public int maxDepth(TreeNode root)
//如果节点为空,就返回0
if(root == null) return 0;
//递归求左子树的高度
int leftHeight = maxDepth(root.left);
//递归求右子树的高度
int rightHeight = maxDepth(root.right);
//判断差值符合条件 且 左子树高度和右子树高度都>=0 则返回节点高度
if(leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <=1)
return Math.max(leftHeight,rightHeight) + 1;
else
//如果不是平衡二叉树就返回-1
return -1;
public boolean isBalanced(TreeNode root)
//如果为负数就是false
return maxDepth(root) >= 0;
第八题: 对称二叉树
LeetCode 101: 对称二叉树
描述:
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
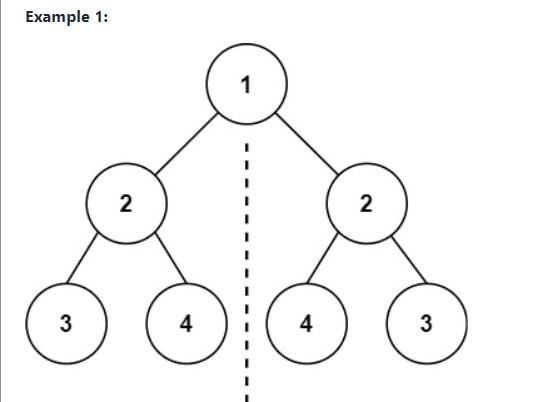
解题思路:
1. 递归解题,思路: ①.如果根节点为空,那么就对称. ②判断根节点的左右子树是否是对称
2. 判断是否对称的方法,如图可以看出,左子树的左孩子和右子树的右孩子相等,左子树的右孩子 和 右子树的左孩子相等.那么就是对称.
3. 由此可以利用第四题,相同的树的代码来实现.
4. 第四题是判断两个节点的左子树是否相同,此题只需要修改判断左子树的左节点,和右子树的右节点是否相同即可.
代码实现:
class Solution
public boolean isSameTree(TreeNode p,TreeNode q)
//如果两个节点同时为空,就是对称
if(p == null && q == null) return true;
//如果两个节点有一个为空,另一个不为空,则不对称
//如果两个节点的值不相等就不对称.
if(p == null || q == null || p.val != q.val) return false;
// 判断左子树的左孩子和右子树的右孩子是否相等.
// 判断左子树的有孩子和右子树的左孩子是否相等.
return isSameTree(p.left,q.right) && isSameTree(p.right,q.left);
public boolean isSymmetric(TreeNode root)
return isSameTree(root.left,root.right);
第九题: 二叉树的镜像
NC72 : 二叉树的镜像
描述:
操作给定的二叉树,将其变换为源二叉树的镜像。
数据范围:二叉树的节点数 0≤n≤1000 , 二叉树每个节点的值0≤val≤1000
要求: 空间复杂度O(n) 。本题也有原地操作,即空间复杂度O(1) 的解法,时间复杂度O(n)
比如:
源二叉树

镜像二叉树
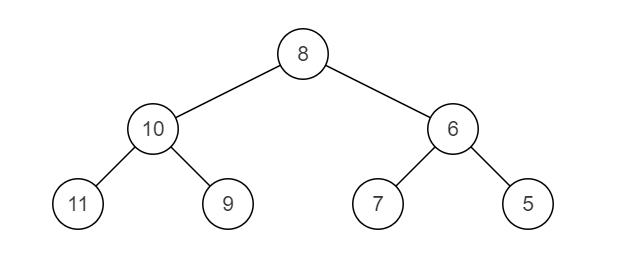
解题思路:
1. 求镜像二叉树,让左右子树交换,再让左右子树的左右子树交换,递归这个思路就行,
2. 情况一 节点为空,直接返回空节点
3. 情况二 只有该节点,没有子节点,直接返回该节点.
4. 不符合这两种情况就交换节点,然后进入递归.
代码实现:
public TreeNode Mirror (TreeNode pRoot)
// 节点为空 直接返回
if(pRoot == null) return pRoot;
// 当前节点没有左右节点,直接返回该节点
if(pRoot.left == null && pRoot.right == null) return pRoot;
// 交换左右节点
TreeNode tmp = pRoot.left;
pRoot.left = pRoot.right;
pRoot.right = tmp;
// 处理左子树
Mirror(pRoot.left);
// 处理右子树
Mirror(pRoot.right);
return pRoot;
进阶面试题
第一题: 二叉树的构建及遍历。
牛客: 二叉树遍历
描述:
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串:ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。