Paddle 网络中的Tensor 数据结构
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Paddle 网络中的Tensor 数据结构相关的知识,希望对你有一定的参考价值。
简 介: ※Tensor是Paddle深度框架中的重要概念。对于 Tensor概念介绍-使用文档-PaddlePaddle深度学习平台 文档中的概念进行学习和测试,对比了Tensor于numpy中的ndarray之间的差异。
关键词: Tensor,numpy,paddle
§01 Tensor基本概念
一、基本特征
1、Tensor概念
飞桨(PaddlePaddle,以下简称Paddle)和其他深度学习框架一样,使用Tensor来表示数据,在神经网络中传递的数据均为Tensor。
Tensor可以将其理解为多维数组,其可以具有任意多的维度,不同Tensor可以有不同的数据类型 (dtype) 和形状 (shape)。
同一Tensor的中所有元素的dtype均相同。如果你对 Numpy 熟悉,Tensor是类似于 Numpy array 的概念。
(1)所有Tensor属性
Tensor的属性很多,下面列出了一个普通的Tensor的所有的参数。
T __add__ __and__ __array__ __array_ufunc__ __bool__
__class__ __deepcopy__ __delattr__ __dir__ __div__ __doc__
__eq__ __float__ __floordiv__ __format__ __ge__ __getattribute__
__getitem__ __gt__ __hash__ __index__ __init__ __init_subclass__
__int__ __invert__ __le__ __len__ __long__ __lt__
__matmul__ __mod__ __module__ __mul__ __ne__ __neg__
__new__ __nonzero__ __or__ __pow__ __radd__ __rdiv__
__reduce__ __reduce_ex__ __repr__ __rmul__ __rpow__ __rsub__
__rtruediv__ __setattr__ __setitem__ __setitem_varbase__ __sizeof__ __str__
__sub__ __subclasshook__ __truediv__ __xor__ _alive_vars _allreduce
_bump_inplace_version _copy_to _getitem_from_offset _getitem_index_not_tensor _grad_ivar _grad_name
_grad_value _inplace_version _is_sparse _place_str _register_backward_hook _register_grad_hook
_remove_grad_hook _set_grad_ivar _set_grad_type _share_memory _to_static_var abs
acos add add_ add_n addmm all
allclose any argmax argmin argsort asin
astype atan backward bincount bitwise_and bitwise_not
bitwise_or bitwise_xor block bmm broadcast_shape broadcast_tensors
broadcast_to cast ceil ceil_ cholesky chunk
clear_grad clear_gradient clip clip_ clone concat
cond conj copy_ cos cosh cpu
cross cuda cumprod cumsum detach diagonal
digamma dim dist divide dot dtype
eig eigvals eigvalsh equal equal_all erf
exp exp_ expand expand_as fill_ fill_diagonal_
fill_diagonal_tensor fill_diagonal_tensor_ flatten flatten_ flip floor
floor_ floor_divide floor_mod gather gather_nd grad
gradient greater_equal greater_than histogram imag increment
index_sample index_select inplace_version inverse is_empty is_leaf
is_tensor isfinite isinf isnan item kron
less_equal less_than lgamma log log10 log1p
log2 logical_and logical_not logical_or logical_xor logsumexp
masked_select matmul matrix_power max maximum mean
median min minimum mm mod multi_dot
multiplex multiply mv name ndim ndimension
neg nonzero norm not_equal numel numpy
persistable pin_memory place pow prod qr
rank real reciprocal reciprocal_ register_hook remainder
reshape reshape_ reverse roll round round_
rsqrt rsqrt_ scale scale_ scatter scatter_
scatter_nd scatter_nd_add set_value shape shard_index sign
sin sinh size slice solve sort
split sqrt sqrt_ square squeeze squeeze_
stack stanh std stop_gradient strided_slice subtract
subtract_ sum t tanh tanh_ tensordot
tile tolist topk trace transpose trunc
type unbind uniform_ unique unique_consecutive unsqueeze
unsqueeze_ unstack value var where zero_
(2)显示属性的内容
import matplotlib.pyplot as plt
from numpy import *
import math,time
strid = 5
tspgetdopstring(-strid)
itemall = clipboard.paste().replace('[','').replace(']','').replace("'","").replace(' ', '').split(',\\r\\n')
maxlen = max([len(s) for s in itemall])//2
forms = ':%d'%maxlen
itemall = [forms.format(l) for l in itemall]
itemall = list(zip(*([iter(itemall)]*6)))
for i in itemall:
print(" ".join(i))
2、Tensor创建
(1)通过List创建Tensor
ndim_1_tensor = paddle.to_tensor([2.0, 3.0, 4.0], dtype='float64')
print(ndim_1_tensor
Tensor(shape=[3], dtype=float64, place=CPUPlace, stop_gradient=True,
[2., 3., 4.])
从上面来看出,Tensor的属性中的确很多,但print出来的性质主要包括:
- shape
- dtype
- palce
- stop_gradient
(2)通过单个数值创建Tensor
print(paddle.to_tensor(100, dtype='float64'))
print(paddle.to_tensor([100]))
Tensor(shape=[1], dtype=float64, place=CPUPlace, stop_gradient=True,
[100.])
Tensor(shape=[1], dtype=int64, place=CPUPlace, stop_gradient=True,
[100])
(3)通过二维数组创建Tensor
通过ndarray二维数组可以建立二维的Tensor。
Ⅰ.第一个例子
a = random.randn(5,5)
print(a)
print(paddle.to_tensor(a,dtype='float64'))
[[-0.38842275 0.60203552 0.75242934 -0.63579722 -0.98777417]
[ 0.13979701 -0.54047714 -0.05141568 0.40233249 0.91852057]
[ 1.42899054 -0.94539537 0.37745157 0.94664502 2.17836026]
[ 0.07094955 0.60793962 -0.080198 -0.71505243 -0.23229649]
[-2.60935282 0.66411124 -1.90732575 -0.22735439 1.40916696]]
Tensor(shape=[5, 5], dtype=float64, place=CPUPlace, stop_gradient=True,
[[-0.38842275, 0.60203552, 0.75242934, -0.63579722, -0.98777417],
[ 0.13979701, -0.54047714, -0.05141568, 0.40233249, 0.91852057],
[ 1.42899054, -0.94539537, 0.37745157, 0.94664502, 2.17836026],
[ 0.07094955, 0.60793962, -0.08019800, -0.71505243, -0.23229649],
[-2.60935282, 0.66411124, -1.90732575, -0.22735439, 1.40916696]])
Ⅱ.第二个例子
ndim_3_tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
print(ndim_3_tensor)
Tensor(shape=[2, 2, 5], dtype=int64, place=CPUPlace, stop_gradient=True,
[[[1 , 2 , 3 , 4 , 5 ],
[6 , 7 , 8 , 9 , 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
Ⅱ.第三个例子
ndim_3_tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
print(ndim_3_tensor)
Tensor(shape=[2, 2, 5], dtype=int64, place=CPUPlace, stop_gradient=True,
[[[1 , 2 , 3 , 4 , 5 ],
[6 , 7 , 8 , 9 , 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
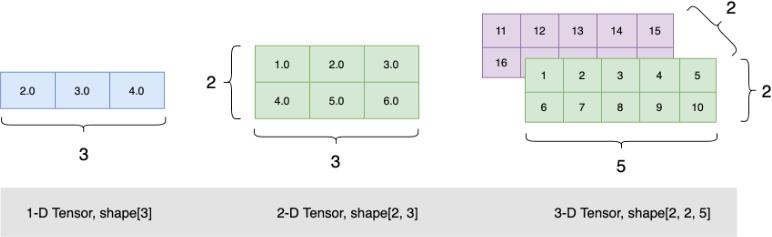
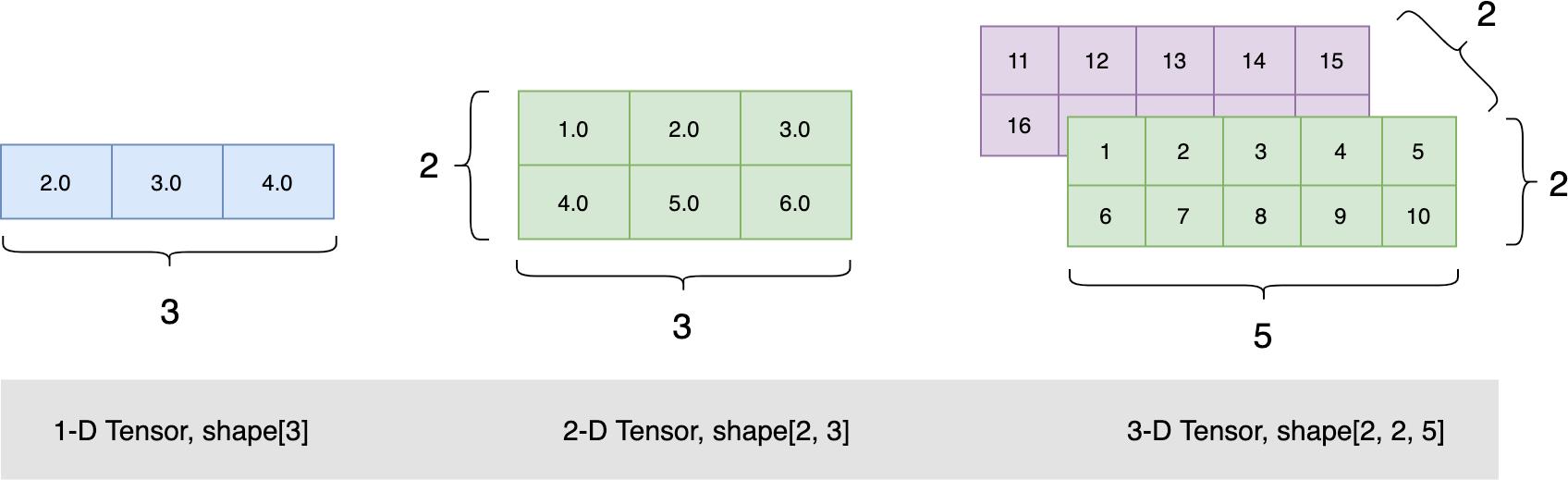
▲ 图1.1.1 不同ndim的Tensor
3、Tensor转换为Numpy array
ndim_2_tensor.numpy()
print(ndim_3_tensor.numpy())
[[[ 1 2 3 4 5]
[ 6 7 8 9 10]]
[[11 12 13 14 15]
[16 17 18 19 20]]]
4、转换Tensor问题
Tensor必须形状规则,类似于“矩形”的概念,也就是,沿任何一个轴(也称作维度)上,元素的数量都是相等的,如果为以下情况:
ndim_3_tensor = paddle.to_tensor([[[1, 2, 3, 4],
[6, 7,